摘　要: 以分层递阶智能控制为基础框架，提出了基于控制任务的某些时域性能指标的智能控制任务适应算法，对运行控制级动态建立特征模型，迫使系统逼近理想控制轨迹，从而提高控制性能。
　　关键词: 智能控制 任务自适应 特征模型 上(下)界特征直线 特征点

　　实际系统由于存在非线性、不确定性、时变性和不完全性等因素，一般无法获得系统精确的数学模型，而且为了提高控制性能，整个系统变得较为复杂，增加了设备的初投资，降低了系统的可靠性。在这种背景下，无需人的干预就能自主地驱动智能机器实现其目标的智能控制诞生了。直到目前，传统控制理论中的各种动态性能指标只能作为智能控制的事后评价标准，无法作为智能控制系统的设计依据。
　　Saridis曾提出智能控制系统的分层递阶结构，奠定了智能控制的三元结构的理论基础^[1]。在此基础上，周其鉴、李祖枢等人提出仿人智能控制(HSIC)，并建立了仿人智能控制的基本理论，给出了仿人智能控制器的设计方法^[2][3]。李祖枢、涂亚庆等提出的设计方法以相平面(e－e′)作为信息空间设计控制器。由于相平面(e－e′)只是隐含了时间信息，难以与性能指标建立直接联系，因此这是一种定性的设计方法。然而控制系统设计的目标，总是针对控制系统完成的任务，满足于特定的性能指标^[4]。基于这种思想，本文提出了面对不同任务的某些时域指标，按照分层递阶控制的框架，以(e－t)为信息空间设计智能控制器的方法，并给出了任务适应算法。由于(e－t)信息空间明显包含了e′的信息，并且可以直接与时域性能指标相联系，因此，该设计方法是一种定性与定量相结合的设计方法。
1 智能控制任务适应的基本思想
　　按照分级递阶智能控制的基本理论，整个系统由中枢司令级、组织协调级和单元控制级构成。单元控制级又可分解为任务适应级(TA)、参数校正级(ST)和运行控制级(MC)。运行控制级直接面向被控对象，采用产生式系统结构。知识库用三重序元＜Φ，Ψ，Ω＞描述。其中，Φ＝{Φ₁，Φ₂，…，Φ_n}称为特征模型，Ψ＝{Ψ₁,Ψ₂,…，Ψ_r}称为控制(决策)模态集，Ω＝{ω₁，ω₂，…，ω_q}为产生式集。产生式ω_i(i＝1，2，…，q)可表示为
　　IF Φ_i THEN Ψ_i, Φ_i∈Φ， Ψ_i∈Ψ
　　其中Φ_i称为特征状态，是特征信息空间划分的一个区域；Ψ_i是控制器的输出量U与输入信息R、特征记忆Λ之间定量或定性关系的描述。
　　MC级的控制目标主要是控制精度，即满足特定任务的某些时域性能指标。为了适应不同的任务，满足相应的性能指标，MC级的知识库＜Φ，Ψ，Ω＞应该适应不同的任务。
　　无论是定值控制还是伺服控制，控制过程总是期望系统的动态响应在时相空间(e－e′－t)为一条理想轨迹。换言之，这条理想轨迹作为设计智能控制器的目标，轨迹上的每一点都被视为控制过程中的瞬态指标。这条理想轨迹可以分别向(e－t)、(e′－t)和(e－e′)三个平面投影，根据分析的侧重点考虑这三条投影曲线中的一条或几条，从而简化设计目标。由于被控对象具有不确定性且又不确知，实际上运动的轨迹只可能处在这条理想曲线周围的一个曲柱中。智能控制器的设计任务就是以实际轨迹与理想轨迹在信息空间中的偏差轨迹为依据，对信息空间(e－e′－t)进行划分(特征模型)，并给出相应的控制模态。
　　在HSIC的基本算法中，特征模型的建立即特征状态的划分是一种近乎先验的过程^[2][3]。换言之，特征变量的阈值确定是纯粹的经验判断，它不依对象的不同而自动设置，也不会根据实际过程的输出响应和偏差曲线做动态调整，更无法依据控制指标的要求变化而适应。这在相当大的程度上限制了控制任务的正确完成。本文提出的动态建立特征模型的算法是一种任务自适应的方法。根据系统的瞬态性能指标的要求，在线辨识出过程的纯时延，结合上升时间t_r、超调量δ_p和峰值时间t_p划分(e－t)平面，实时给出MC级特征状态的切换阈值，动态地建立其特征模型Φ，改变其知识库，迫使控制沿着适当的轨迹达到各项控制指标。基于这种思想，通过对控制的偏差曲线进行几何分析，给出任务适应级TA对MC级特征基元的实时调整方法。
2 任务适应算法及仿真实验
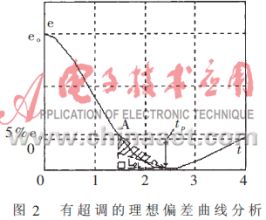
　　对于限制上升时间t_r、超调量δ_p和峰值时间t_p的伺服跟踪控制系统，我们考虑稳态误差e_ss＝e(∞)×5%的性能要求，如图1所示。引入上升时间特征点A、第一上界特征直线L_1u、第一下界特征直线L_1l三个概念，并由此导出HSIC的任务适应算法，确定对信息空间划分的特征模型。考虑上升时间t_r、超调量δ_p和峰值时间t_p的要求，进一步引入峰值特征点B、第二上界特征直线L_2u和第二下界特征直线L_2l的概念，如图2所示。

　　我们以直线L_1u作为特征变量的阈值轨迹之一。只要实际偏差e(t)在时段(0,t_r)内的值都在直线L_1u的下方，就可以确保满足性能指标上升时间t_r。我们把直线L_1l定义成特征变量的阈值轨迹，其目的是满足t_r的同时，使系统的输出响应尽量避免超调。于是规定理想偏差曲线e₁(t)介于L_1u和L_1l两条直线之间，即图1中的阴影区域内。
　　类似地，对于时间段(t_r,t_p)，理想偏差曲线e₂(t)应介于特征直线L_2u和L_2l之间，如图2中的阴影区域所示。在上述定义的特征点、特征直线的基础上，对信息空间进行划分，建立相应特征模型如下：
　　Φ₁＝{Φ₁，Φ₂，Φ₃，Φ₄，Φ₅，Φ₆，Φ₇}
　　
　　这里对于Φ₂、Φ₅和Φ₇可以采用保持控制模态。
　　类似地，还可以对时间段(t_p,∞)的偏差曲线做进一步分析。需要指出，这里定义的第一、二下界特征直线是经验直线，根据现场专家对于控制环境和对象的了解来确定。出于简化考虑，本文将这条阈值轨迹设定为角平分线。
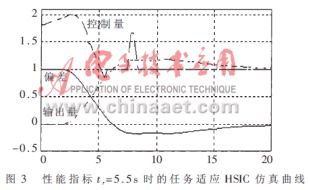
　　设受控对象传递函数为，输入为单位阶跃函数，性能要求是上升时间t_r＝5.5s，超调量δ_p＝20%,峰值时间t_p＝9s。
　　仿真结果如图3所示，表明本文提出的任务适应算法能够较好地满足控制性能指标的要求，具有很强的任务适应性。如果通过ST级对MC级控制模态中的控制参数进行在线校正，控制效果会更好。