神经振荡器是一种能够在缺乏感官反馈或者高级控制命令的情况下，通过协调模式自发地产生规律输出的神经电路。神经振荡器已经被广泛地应用于机器人的智能控制与生物研究中[1]，成为国内外的研究热点。相比于软件编程，神经振荡器的硬件实现具有高速、并行处理、抗干扰等优点，更接近于其原有的生物特性，因此引起了许多研究者的关注。在近些年来，许多神经振荡器的硬件实现工作是基于模拟器件完成的[2-3]。虽然模拟电路能够与生俱来地实现够非线性函数，其功耗也相对较低，但与可编程逻辑器件（FPGA）相比，基于超大规模集成电路(VLSI)的工作需要相对长的设计周期，同时缺乏灵活性和兼容性。另一方面，FPGA已经被广泛地应用于人工神经网络(ANN)和智能控制电路硬件的实现[4-5]，但基于FPGA的神经振荡器实现国外才刚刚开始，国内尚未见报道。且之前的工作大多基于乘法器的直接实现方法[6]，未能充分利用FPGA的资源。
1 神经振荡器及其应用
    神经振荡器是一种耦合振荡系统，通过神经元之间的相互抑制实现稳定的相位互锁，并产生自激振荡激发肢体做节律运动[7]。在仿生机器人控制中，被控制对象往往存在非线性、系统工作点变化剧烈等特点，传统的控制往往是建立在单纯依靠严格和精确数学模型基础上，但这种方法已难以满足复杂多变且环境未知的机器人控制需求[8]。同时，基于模型的机器人控制方法模型复杂、解不唯一、非结构环境适应性较差等，不利于实现仿生机器人的快速稳定运动[9]。神经振荡器具有非线性耦合的优点，很适合仿生机器人的节律运动控制，能达到快速稳定的效果。此外，可以通过调整有限的神经振荡器参数，建立满足具体要求不同的机器人与外界环境交互的复杂运动学、动力学模型，而不需要对整个系统建模，机器人的控制难度降低。总之，基于神经振荡器控制的机器人具有以下优点：（1）自动稳定性；（2）较强的环境适应性；（3）参数化建模[8-9]。
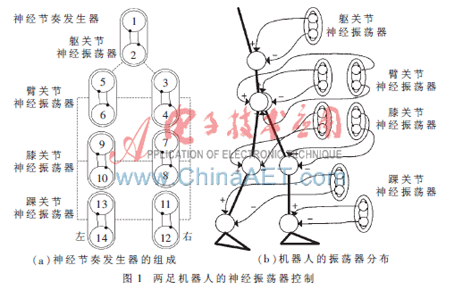
    图1为神经振荡器应用于两足机器人的一个例子。该两足机器人包含七个关节，其中包括一个躯关节（也可称之为腰关节）、两个臀关节、两个膝关节和两个踝关节[10]。每一个神经振荡器由一对相互抑制的神经元构成，每个关节由一个神经振荡器控制。这样，就可以将两足机器人转化为七个神经振荡器控制的神经模式发生器系统，图1（a）所示为模式发生器系统的组成。通过调整振荡器的参数，使各关节协调地做振荡运动，可以实现两足机器人稳定地行走等运动。

2 分布式算法的改进
    传统的分布式算法要求输入为小数或整数。在FPGA系统中，一般的输入信号通过二进制小数点转换模块转换为纯小数(或者是整数)，输出则刚好相反。本文对分布式算法做了修改，使其不需要小数点转移过程。对于某一有符号的定点数xk，若其同时包含整数部分和小数部分，xk可以用一个二进制数bN-1，…，b1，b0，b-1，…，b-M表示（共N+M=Q位，N位整数位，M位小数位）。bk，N-1为符号位，当bk，N-1=1时，xk为负数，bk，N-1=0时，xk为正数；bk，m为最低有效位，代表xk能达到的最高精度。
    
    同传统的分布式方法一样，这里的Lm事先输入到查找表中，通过加权累加器对查找表的输出进行变更、求和。对于K个输入且输出为y的分布式算法的原理如图2所示[10]。

    分布式算法按时间周期进行运算。一个时钟周期是指变量xk的二进制编码依次输入到查找表（LUT）中累加求和所用的时间。一个时钟周期包含M个时段，每时段输入二进制的一位，第m=M-1位最先输入，第m=0位最后输入。每输入一位，通过加权累加器求和。m=0的时间段称为符号位时间，其余时间段为非符号位时间。一个时钟周期包括符号位时间和非符号时间，当符号位时间到来并结束，代表一个时间周期的结束和下一个时间周期的开始，如图2所示，符号时间结束，开关从位置①打到位置②，同时输出y值。
3 基于分布式算法的神经振荡器
    神经振荡器的设计可以在多个层次实现，如生物模型、类神经网络模型和耦合振荡器[1]。最广泛使用的是神经振荡器，其实质是交互抑制的非线性耦合振荡器。常见的耦合振荡器模型有Amari-Hopfield、Van De Pol和Matsuoka等，这些模型遵循相似的原理。例如，Amari-Hopfield振荡器[2]的动力学方程如下式所示：
  
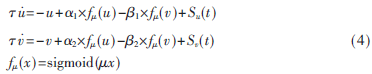
其中，u和v为神经元的输出；Su(t)和Sv(t)为外部输入；α1、α2、β1、β2、μ为控制参数；fμ(x)为传递函数。如式(4)所示，振荡器的实现需要几个基本操作：加减、乘、积分求导和传递函数（可选）。一个单独的振荡器只需要几个乘法器。然而，更大的振荡器网络需要更多抑制路径与更多的乘法器来实现,如果要实现一个7自由度的双足机器人控制系统，将会需要上百的片上乘法器，资源消耗十分巨大；另一方面，大多数FPGA有大量的查找表（LUT）资源。为了提高乘法效率，引入了分布式算法（DA）来优化神经振荡器的FPGA实现，分布式算法利用了查找表而并非乘法器。关于传递函数的FPGA实现问题，Tommiska已经做了详细的讨论[11]。在这里使用饱和函数来取代双级sigmoid函数。两者的曲线图十分相近，将式（4）中传递函数f?滋(x)用饱和函数代替，替换后的振荡模型的质量没有明显降低。
    
根据以上的方程，可以方便地算出查找表的内容，在这里不再赘述。
4 分布式神经振荡器的FPGA硬件实现
    在Matlab/Simulink环境下，使用Altera公司提供的DSP Builder工具箱[12]对基于分布式算法的神经振荡器进行建模，按照式（5）在Simulink中组建模块，得到的分布式神经振荡器的结构。该系统主要包含了DA分布式算法、adder加法器、integrator积分器、transfer传递函数4个子模块，系统采用20位定点数据的表述形式（整数部分为8位）。
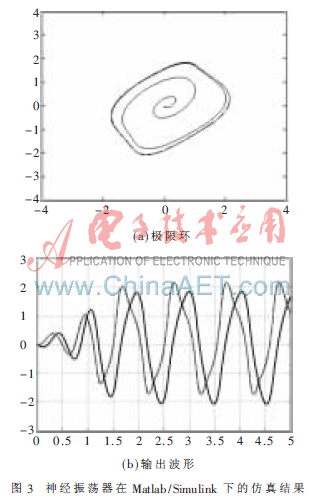
    Matlab/Simulink环境下仿真结果的极限环吸引子如图3(a)所示。其表明，对于从静止状态开始运动的神经振荡器，经过有限的时间，最终会处于李雅普诺夫意义下的稳定，即神经振荡器处于稳定的振荡过程而能量不衰减。u和v的输出波形如图3(b)所示。经过约20 ?滋s的时间，神经振荡器进入稳定的振荡过程。

    通过系统仿真，该神经振荡器已达到设计要求，将模型文件.mdl转化为硬件描述语言文件.vhd，并对其综合。之后，在QuartusⅡ环境中打开由DSP Builder建立的QuartusⅡ工程文件，就可以对生成的VHDL代码进行器件配置、引脚设定、硬件下载等工作。当然，该系统还可以作为制定硬件模块被集成到NIOS II 软核中，以方便对其调用与配置。
5 实验
    将程序下载到工作频率为50 MHz的Altera Cyclone II EP2C8Q208芯片上。通过Signal Tap II逻辑分析仪，获得实验数据，并将其导入Matlab中进行处理、分析。计算可得，u相输出的实验与仿真结果相关系数为0.99，v也为0.99，可见实验结果和仿真结果高度一致，验证了实验的准确性。
    据分析，分布式算法节省了74%的查找表（LUT），75%的逻辑寄存器和100%的嵌入式乘法器。可见，基于分布式算法的神经振荡器，显著地节约了硬件资源。
    本文针对FPGA有限的算术乘法器提出了一个高效的神经振荡器实现方案。首先将分布式算法进行了改进，使其可以直接处理同时带有整数位和小数位的输入信号，并将改进的分布式算法应用到神经振荡器中。在Matlab/Simulink环境下，通过DSP Builder建立了系统模型。在保证了精确的实验结果同时，与传统的基于乘法器相比，该方案显著地节约了硬件资源。此外，此方法还可以被应用到其他需要大量乘法运算的FPGA系统上，如人工神经网络或者智能控制系统。
参考文献
[1] IJSPEERT A J.Central pattern generators for locomotion  control in animals and robots：A review[J].Neural Net  works，May 2008(21)：642-653.
[2] NAKADA K，ASAI T，AMEMIYA Y.An analog CMOS central pattern generator for interlimb coordination in  quadruped locomotion[J].IEEE T Neural Networ，2003(14)：1356-65.
[3] VOGELSTEIN R J，TENORE F V G，GUEVREMONT L，et al.A silicon central pattern generator controls locomotion in  Vivo[J].IEEE T Biomed Circ S.2008(2)：212-22.
[4] MISRA J，SAHA I.Artificial neural networks in hardware：a survey of two decades of progress[J].Neurocomputing.2010(74)：239-55.
[5] MONMASSON E.FPGAs in industrial control applications[C]. Industrial Informatics，IEEE Transactions on.2011.
[6] TORRES H C，GIRAU B.Implementation of central pattern generator in an FPGA-based embedded system[A].Artificial Neural Networks-ICANN.2010，6353：276-285.
[7] 李彬.基于Wilson Cowan神经振荡器的四足机器人步态规划研究[J].山东大学学报，2010，1(40)：6-9.
[8] 李宏凯，孙久荣，戴振东.动物运动指令的中枢模式发生器[J].机器人，2008，3(37)：279-288.
[9] GENTARO T.A  model  of  the  neuro-musculo-skeletal system  for  human  locomotion[J].Biological Cybernetics，1995(73)：97-111.
[10] STANLEY A W.Applications of distributed arithmetic to digital signal processing：a tutorial review[J].IEEE ASSP Magazine，1989：4-15.
[11] TOMMISKA M T.Efficient digital implementation of the sigmoid function for reprogrammable logic[J].IEE P-Comput Dig T，2003：403-411.
[12] 张志亮，赵刚，齐星刚.从Simulink模型自动生成VHDL代码—基于DSP Builder的FPGA设计流程[J].自动化技术，2004(23)：4-6.