0 引言

　　计算机仿真是电路设计的一个重要环节。一方面它是可以代替采用简化电路模型估算电路特性进行验证的传统设计方式， 能高效地进行电路参数的确定和方案的优选， 并在设计初期对产品的性能进行可靠的预测， 从而提高设计质量， 缩短设计周期， 节省设计费用，故已成为现代设计方法中必不可少的组成部分； 另一方面， 它能利用仿真软件得出电路性能受电路中关键参数的影响， 更好地掌握电路的特性和指标， 对实际电路调试工作具有指导意义。本文以CCⅡ低通滤波器的设计为例， 先采用理论分析设计低通滤波电路， 然后运用OrCAD/ Pspice 进行仿真分析和优化设计， 最后对设计结果进行验证， 以使电路性能达到设计要求。同时， 也便于了解该电路受参数变化的影响及其高低温情况下的性能变化等特性。

　　1 滤波电路的设计

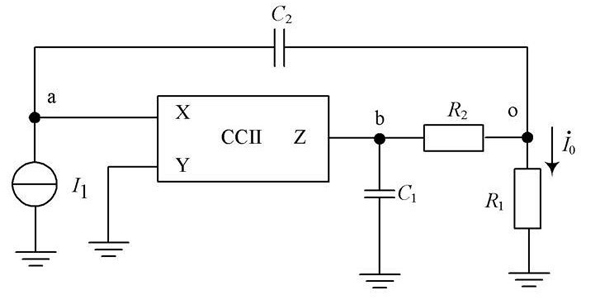
图1 基于CC Ⅱ的低通滤波电路

　　一般地， 图1 所示电路的转移函数可以通过列写电路节点a, b, o 的电流方程来求得， 即对a 节点有：

　　式中： K 为CCⅡ的电流放大倍数。联系以上等式可以求得图1 所示电路的转移函数为：

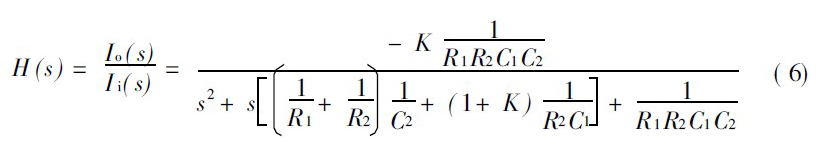
　　由图1 所示电路的转移函数可以得出电路参数与元件值的关系：

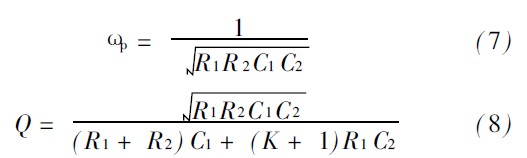
　　这种设计方法的主要思路是通过令R1 = R2 = R ,C1 = C2 = C 来减小元件的分散性， 然后根据式（ 7） ,式（ 8） 进行设计， 从而确定每个元件的参数值， 其设计步骤如下：

　　（ 1） 令R1 = R2 = R, C1 = C2 = C, 并选取适当的C 值；

　　（ 2） 根据给定的ωp 和式（ 7） , 求出R;

　　（ 3） 根据给定的Q 值和式（ 8） , 求出K ;

　　（ 4） 进行PSpice 仿真分析以及优化设计。

　　设计指标为： f p = 105 Hz, Q = 1/ √2。

　　根据电路参数与元件值的关系以及设计步骤选取C = 1 nF, 则可求得： R = 10 k , K = √2 - 3。

　　2 电路的PSpice 仿真分析与优化

　　首先对原始电路设计方案在OrCAD/ Capture 下绘图， 其中CCⅡ的仿真模型采用子电路形式， 所有元件都调用PSpice 仿真库中的模型， 选电流源为交流源，交流电路为1 A, 直流电流为0 A , 设电容C1 和C2 的初始值为0; 分析类型为AC Sw eep/ Noise, 起始频率为10 Hz, 终止频率为100 MHz, 扫描记录点数为1 000; 扫描类型为Log arithmic, 扫描方式为Decade, 以此进行电路仿真， 得到的电路初始幅频特性曲线如图2所示。从电路的转移函数可知， 图1 所示的滤波器为二阶低通滤波器， 对比二阶低通滤波器的幅频特性可以得知， 其原始电路的设计指标不符合要求。

图2 输出电流I o 的频率特性曲线

　　2. 1 电路参数分析

　　对原电路进行参数扫描分析时， 可将基本特性分析类型设置为AC Sw eep/ Noise 进行分析， 其他参数设置相同， 每次分别将R1 , R2, C1, C2 设置为全局变量进行参数扫描分析， 仿真分析结果如图3所示。此时， R1 =R2 = 10 kΩ, C1 = 10 pF, C2 = 10F。

图3 参数扫描分析后Io 的频率特性曲线。

 　　2. 2 电路优化设计

　　PSpice A/ A是OrCAD 高级版本新增加的高级分析工具， 包含Sensit iv ity , MONte Carlo, Smoke, Optimizer, Paramet ric Plo tter A nalysis 等高级分析功能， 它可在PSpice A/ D 分析的基础上， 最大程度地提高所设计电路的性能及可靠性。灵敏度分析是电路优化设计的第一步， 往往需要将分析结果传给优化设计工具Opt imizer。灵敏度分析的步骤如下：

　　（ 1） 绘制电路图， 绘制电路图的元件取自专供PSpice A/ A 使用的“advance”文件夹， 并采用变量表设置元件参数；

　　（ 2） 执行PSpice 分析， 确定电路的性能指标；

　　（ 3） 使用灵敏度工具Sensit iv ity 进行灵敏度分析，将程序运行结果传给Opt imizer。

　　由运行结果可知， 对电路指标最敏感的元件是R1和C1。可以调用PSpice A/ A 中的优化设计Opt imizer模块对电路中最敏感的元件参数进行调整。

　　电路的优化设计实际上是一个约束优化问题， 是在电路特定拓扑和元器件参数范围的约束下， 通过调整元器件的值来使电路特定性能指标达到最优。优化设计的步骤如下：

　　（ 1） 启动优化器Opt imizer;

　　（ 2） 设置优化变量， 即设置待优化的元件参数， 通常选择相对于该性能指标中灵敏度影响较大的元件参数作为优化参数；

　　（ 3） 选择需要优化的元件；

　　（ 4） 设置优化目标函数， 还需设定性能指标的变化范围， 即在MIN 框中指定目标函数的最小值， 在MAX框中指定最大值， 在Weig ht 框中指定权重；

　　（ 5） 执行优化分析设计。优化后的电路元件参数约为： R1= R2 = 65 kΩ , C1= 10 pF, C2 = 10F, 优化后的特性曲线如图4 所示。

图4 优化后低通滤波器的特性曲线

　　调用OrCAD/ PSpice 的函数功能可以从图4 所示的特性曲线中得到滤波器电路的各项特性参数。其中，3 dB带宽为250. 642 86 kHz; Q 值为1. 010 09; 中心频率为106. 025 22 kHz; 3 dB 截止频率为274. 568 34 kHz。

　　从上述参数可以看出， 优化后的电路性能基本上（ qudiao） 符合设计指标的要求， 同时还有一定的裕度。

　　2. 3 温度扫描分析

　　在实际电路中， 电阻阻值以及晶体管的许多模型参数值都与温度的关系非常密切， 温度变化必然通过这些元器件参数值的变化引起电路特性的变化。通过OrCAD/ Pspice 中的温度扫描分析能够模拟电路输出特性受温度变化的影响。为了设置元件的温度系数，Pspice 提供了一个专门的元件库breakout . olb, 库中元件的名称为其关键字后加“break”, 可用该元件库中的元件修改线路图， 选中需设置温度系数的元件， 再选择菜单Edit \ PSpice mo del, 程序将弹出Pspice Model Editor 模型编辑器， 这样就可以在Pspice model 窗口中设置相应的温度系数。一般将其模型参数设置为：

　　“ . MODEL Rbreak RES R = 1 TC1 = 0. 004 TC2 =0. 000 5”即可。其中， Rbreak 是电阻的模型名称， 必须与电路图中的电阻标识一致， 否则就会出错； RES 是电阻模型的关键字； R 为电阻的倍乘系数； T C1 和T C2 分别为电阻的一阶、二阶温度系数。在通常的电路特性分析时， Pspice 的内定温度为27℃ 。图5 给出了经过上述优化后的电路分别在- 20 ℃, - 10℃ , 0 ℃, 10℃ ,20℃ , 50℃ , 80℃ , 100℃ 下的滤波器特性曲线。

　　2. 4 Mo nte??Carlo 分析通过优化设计确定电路中每一个元器件的参数值，通常称为标称值。在实际生产中， 按照标称值选用的元器件值不可能完全相同， 而具有一定的离散性。这样，实际组装的电路特性就不可能与标称值模拟的结果完全相同。用PSpice 提供的MonteCar lo 分析能够模拟实际生产中因元器件值的分散性所引起电路特性的分散性。

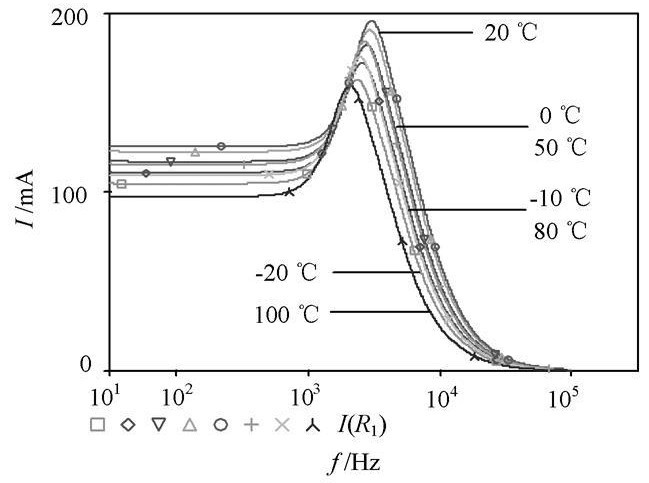
图5 温度扫描时滤波器的特性曲线

　　在进行MonteCarlo 分析之前， 还需要对元器件进行容差设置。元件的容差有器件容差， 批容差和组合容差3 种。其中， 器件容差指可以独立变化的、由同一“ . model”语句定义的容差， 用“DEV” 表示； 批容差指同时变大或变小的容差， 用“LOT”表示； 组合容差指将器件容差与批容差组合起来使用的容差方式。容差设置的方法与温度系数的设置方法类似。

　　Mo nte-Carlo 属于统计分析中的一种， PSpice 中专门提供了统计分析用的元器件符合库breakout . olb。

 　　因此， 调用breakout . olb 中相应的元件即可修改电路图， 打开模型编辑器则可设置元件模型参数， 图1 中的电阻参数设置为： . model Rbr eak RES （ R= 1 DEV =5% ）； 电容参数设置为： . mo del Cbr eak CAP （ C = 1DEV= 10%）； DEV= 10% 表示独立随机变化， 变化范围为10%。电阻独立随机变化服从高斯分布， 容差范围为5% ; 电容独立随机变化也服从高斯分布， 容差范围为10%, 分析次数设为20, 选择AC Sweep/ N oise 分析， 同时设置好其分析参数， 最后进行蒙托卡诺分析， 所得到的3 dB 带宽、中心频率、Q 值、截止频率的直方图分别如图6~ 图9 所示。

　　通过蒙托卡诺分析结果的直方图可以得知， 生产中只要按照Monte??Car lo 分析设定容差所要求选定的相应参数即可。尽管在实际生产中存在元器件参数的分散性， 但产品的成品率还是较高的， 因而具有较好的实用性。

图6 3 dB 带宽分布直方图

图7 中心频率分布直方图

图8 Q 值分布直方图

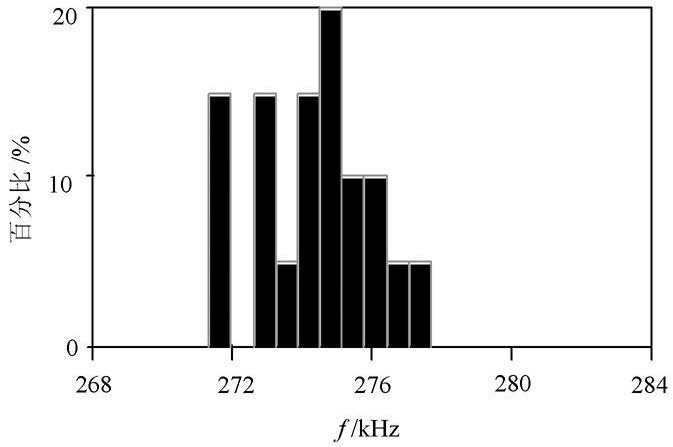
图9 3 dB 截止频率分布直方图

　　2. 5 最坏情况分析

　　最坏情况是一种极端情况， 在实际中出现的概率极低。但是， 最坏情况分析结果却从另外一个方面反映了电路设计的好坏。如果最坏情况的分析结果都能满足性能指标要求或与性能指标要求差距不大， 那么将这种电路设计用于生产时， 电路的质量一定很高。电路中电容、电阻的容差设置同蒙托卡诺分析所得出的在最坏情况下的滤波器特性曲线如图10 所示。

图10 最坏情况下滤波器的特性曲线

　　从该特性曲线可得， 该滤波器在恶劣环境下， 仍能保持良好的中心频率稳定度、3 dB 带宽、Q 值和截止频率。

　　3 结语

　　通过使用OrCAD/ PSpice 仿真分析可以找到滤波电路的最优参数， 并且通过参数扫描分析、温度分析、蒙托卡诺分析、最坏情况分析， 可以得到该滤波器在参数变化、温度变化、参数最恶劣情况下的电路特性， 同时也能获取实际生产中的成品率。而现代电路仿真技术及EDA 技术能够大大缩短整个设计时间， 减少反复设计，节省设计成本。在电路板生产出来之前， 就能获取关于产品成品率、高低温特性以及极端情况下的电路特性，以便能更全面了解电路的性能。因而能够有效提高设计质量以及电路在各种复杂条件下的工作能力， 从而提高成品率。