开关变压器" title="开关变压器">开关变压器的等效电路与一般变压器的等效电路" title="等效电路">等效电路,虽然看起来基本没有区别,但开关变压器的等效电路一般是不能用稳态电路进行分析的;等效负载电阻不是一个固定参数,它会随着开关电源的工作状态不断改变,分布电感与分布电容对正激式开关电源" title="开关电源">开关电源和反激式开关电源工作的影响也不一样.
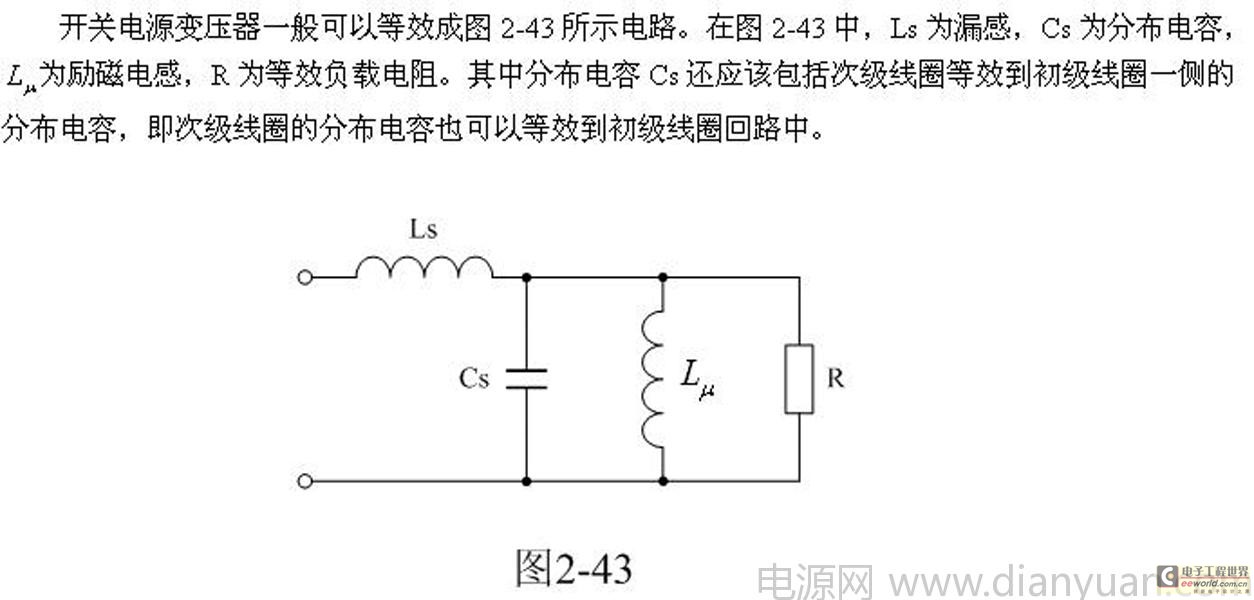

(2-122)式中,Cs为变压器的总分布电容,Cs1为变压器初级线圈的分布电容;C1为次级线圈电路中总电容C2(包括分布电容与电路中的电容)等效到初级线圈电路中的电容;n = N2/N1为变压比。
图2-43开关变压器的等效电路与一般变压器的等效电路,虽然看起来基本没有区别,但开关变压器的等效电路一般是不能用稳态电路进行分析的;即:图2-43中的等效负载电阻不是一个固定参数,它会随着开关电源的工作状态不断改变。
例如,在反激式开关电源中,当开关管导通时,开关变压器是没有功率输出的,即负载电阻R等于无限大;而对于正激式开关电源,当开关管导通时,开关变压器是有功率输出的,即负载电阻R既不等于无限大,也不等于0 。因此,分布电感与分布电容对正激式开关电源和反激式开关电源工作的影响是不一样的。
我们先来看图2-44,当开关管Q1导通时,无论是对正激式开关电源或反激式开关电源,漏感Ls都会对流过开关管Q1的电流Id起到限制作用,即降低Id的电流上升率,这对保护开关管是有好处的;因为,开关管刚导通的时候,电流在管芯内部是以扩散的形式由一个点向整个面扩散的,如果电流上升率太大,很容易使开关管因局部面积电流密度过大造成损伤。
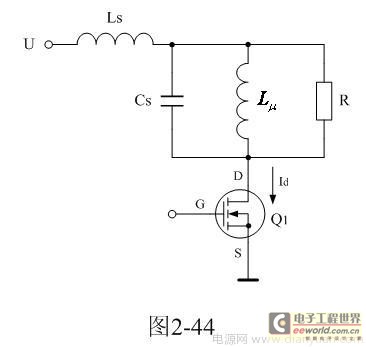
另外,Ls和Cs可以看成是一个串联振荡回路,当开关管Q1开始导通的时候,输入脉冲电压的上升率大于串联振荡回路自由振荡电压的上升率,因此,振荡回路开始吸收能量,输入电压对Ls和Cs进行充电,此时,振荡回路会抑制输入电流上升率的增长;当开关管Q1完全导通以后,开关管完全导通(脉冲进入平顶阶段),相当于输入脉冲电压的上升率为0,此时,输入脉冲电压的上升率小于串联振荡回路自由振荡电压的上升率,因此,振荡回路开始释放能量,振荡回路产生阻尼振荡;
当开关管Q1导通过后,开关管开始关断,相当于输入脉冲电压的上升率为负(脉冲进入反冲阶段),此时,输入脉冲电压的上升率小于串联振荡回路自由振荡电压的上升率,因此,振荡回路又开始再次释放能量,振荡回路再次产生阻尼振荡,如图2-45所示。
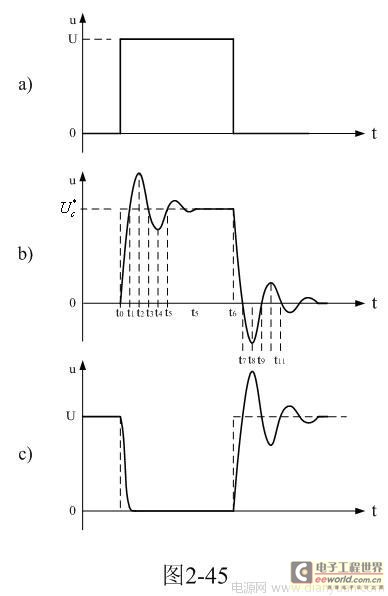
图4-5-a,是电源开关管Q1导通时,输入电压U加于开关变压器两端的波形;图4-5-b,是励磁电感或分布电容两端的电压波形;图4-5-c,是电源关管D、S两极之间的电压波形。
在图4-5-b中,在t0时刻,电源开关管Q1开始导通,输入电压U加于开关变压器两端,输入电压首先通过分布电感Ls对分布电容Cs充电,充电过程是按正弦曲线上升;到t1时刻,流过Ls的电流达到最大值,同时分布电容Cs两端的电压与输入电压U相等,即Ls两端的电压为0;但流过Ls的电流不能为0,Ls将产生反电动势继续给电容Cs充电。
直到t2时刻,流过Ls的电流等于0,电容器Cs充电结束,同时Cs两端的电压也达到最大值;然后电容按正弦曲线开始放电,流过Ls的电流开始反向,到t3时刻,Cs两端的电压又与输入电压U相等,电容停止放电,但流过Ls的电流不能为0,Ls将又产生反电动势给电容Cs进行反向充电,所以Cs两端的电压低于输入电压U。
到t4时刻,流过Ls的反向电流等于0,Cs两端的电压达到最低值;然后输入电压又开始通过Ls对Cs进行充电,到此分布电感Ls与分布电容Cs第一个充放电周期结束。
在t0时刻,由于输入电压的上升率大于分布电感Ls与分布电容Cs充、放电电压的上升率,所以电感和电容是从输入电压吸收能量;在t1时间之后,输入电压的上升率小于分布电感Ls与分布电容Cs充、放电的电压上升率,所以电感和电容是释放能量的,即:电感和电容在t1时间之后会产生阻尼振荡。
这里顺便指出,图2-45-b的波形是很难测量到的,因为它基本上都在变压器内部的分布电感Ls与分布电容Cs之间产生,但它会通过辐射对周边电路造成干扰。
下面我们进一步通过数学的计算方法来对电路进行详细分析。



从(2-128)式可以看出,电容两端电压的变化过程主要由三个与时间常数有关的变量决定。但如果我们直接用(2-128)式来求解(2-125)式,结果将会变得非常复杂,为此我们先对(2-128)式进行简化。


另外,非齐次微分方程(2-125)式的解应该等于齐次微分方程(2-126)式的通解与(2-125)式特解之和。




另外,LC振荡的幅度对于正激式开关电源和反激式开关电源是不同的。对于正激式开关电源,当电源开关管Q1导通的时候,正好开关变压器要向负载输出能量,等效负载电阻R的值相对比较小,即衰减系数很小,LC振荡回路被阻尼得很厉害,因此,振荡幅度下降很快,一般第一个振荡周期过后,振荡回路很难再次振荡起来。

