由于当前计算机网络的飞速发展，入侵检测技术得到了研究者的广泛重视，Forrest[1]等人在1996年首次提出以进程正常运行时产生的一定长度的系统调用短序列作为模型来表现进程正常运行时的状态。Lee[2]等人则用RIPPER从系统调用序列中挖掘正常和异常模式，以规则的形式来描述系统的运行状态，建立了一个更简洁有效的系统正常模型。美国新墨西哥大学的Warrender[3]以系统调用为审计数据，进行了基于隐马尔可夫模型HMM(Hidden Markov Model)的程序行为异常检测研究。美国普渡大学的Lane [4]及其团队则利用了Unix用户的shell命令作为审计数据，进行了基于HMM的用户行为异常检测研究和实验。西安交通大学的周星[5]提出一种利用进程堆栈中的函数返回地址链信息来提取不定长模式的方法，并基于系统调用序列及其对应的不定长模式序列构建了一个两层的HMM来检测异常行为，取得了更低的误报率和漏报率。
    在以上检测方法的基础上，本文提出一种新的基于HMM的用户行为异常检测方法，与参考文献[6]中提出的基于HMM的检测方法相比，检测效率和实时性相对较高，在检测准确率方面也有较大优势。

    本文用一种不同的方法来建立和训练HMM模型，降低不必要的系统占用，并得到一个较好的正常行为模式与异常行为模式的区分效果。
2 基于HMM的用户行为异常检测方法
2.1 数据预处理
    本文所采用的原始数据来自普渡大学的Lane团队，他们花费了很长时间去跟踪了9个Unix用户在2年内的活动记录，以保证这些记录的真实性。
    参考文献[4]对这些数据记录进行了预处理，将每次的命令运用相同的起始、终止符隔开，将各命令中所出现的地址均用统一标识方法代替，所涉及的文件也用相同的标识方法代替，这样的预处理使得原始数据更加整齐且易于分析。在此基础上，本文又作了进一步处理，对于命令行中所有出现的参数进行处理，即将命令中的附加参数与命令本身结合设定为命令序列中的一条命令，而对于地址、网络等记录则直接从命令序列流中删除。表1中左栏的数据流经过本文二次处理后，该命令流序列如右栏所示，左栏中的14条记录经过处理后,减少为右栏中的8条记录，减少了近50%。

    采用本文方法进行数据预处理的依据是：(1)在实际训练及检测中，地址等参数并没有实际意义。无论是按照shell命令序列长度,还是按照各命令本身出现频率作为划分状态标准，都并不需要此类命令内容；(2)当利用大数量的shell命令序列进行建模和检测时，进行这样的二次处理可以降低对系统存储空间的需求。

2.2 HMM建模
    本文所建立的HMM模型的目的是为了描述一个正常用户行为，用W代表合法用户正常行为模式的总类数，而相对应的shell命令集合则如C=(L(1),L(2),…,L(W+1))，其中L(j)为包含若干个长度为l(j)的shell命令序列。W的值越大意味着对于命令集合分类得越精细，所需要的系统资源也就越多。本文针对两种不同的shell命令集合分类方法进行了对比实验，方法一是参考文献[6]中使用的方法；方法二是本文提出的改进隐马尔科夫方法。

    (2)设定W个序列出现频率门限，记为η1,η2,η3,…,ηw，该门限的作用是判定每个Seqmj是否可以成为正常用户行为观测值，低于门限值的即舍去。
　 在C中的L(W+1)用来记录未知和异常模式记录的值，对于L(W+1)下shell命令记录的判定方法为：当l(W)=1时，附加状态W+1对应的观测值集合L(W+1)是由长度为1、且在Sw中出现频率小于门限值?浊w的shell命令序列构成,而当l(W)≠1时,则L(W+1)由所有长度为1的shell命令序列构成。
2.2.2 改进HMM方法
    用户对于日常操作都有一套自己的命令使用频率，本文依据用户与用户之间的命令使用频率差别作为行为分类依据。本文方法中的C表示方法与参考文献[6]中一致，C=(L(1)，L(2),…,L(W+1)),W的值增大，则出现频率的分类更细化，也会增加系统存储和处理量，但与参考文献[6]的状态分类方法相比要小很多。假设正常用户的训练数据为R=(R1，R2，…,Rn)，此时的用户正常行为观测值集合建立起来就相对简单，根据训练数据R，生成W个出现频率分别为l(1),l(2),…,l(W)的shell命令序列流，表示为S1,S2…,Sw，每个Si中包含了所有出现在频率区域的shell命令记录。同样，划分在附加状态W+1下的shell命令序列，也就是未知和异常行为模式的值。
    上述两个建模方法各有利弊，对于参考文献[6]的方法，在利用命令序列长度建模时，其优点是思路清晰，不同的状态之间不会发生重叠，适用性强。缺点是由于每个状态中Si都将存储超过门限值的所有shell命令序列，这将是一个很大的存储量(尤其是当W达到一定值时。而本文方法的，优点是利用命令的出现频率分类，由于命令种类(即便加上了参数)的局限性，所需要的存储量将会少得多，运算起来更快，也更为容易理解。缺点则是对于每个状态对应的频率区域的划分将更多地依赖历史记录和经验。
2.3 HMM的训练
    训练过程也就是参数估计过程，这个过程在研究中是极其重要的，传统的思路是利用Baum-Welch 算法实现，而实际上该算法并不是唯一的，也不是最好的算法。本文采用参考文献[3]提出的改进算法来实现对该HMM模型的训练。
2.4 HMM的检测
    检测阶段的主要工作是对被监测用户在被监测时间内执行的shell命令行进行处理,并利用在训练中已产生的HMM模型,计算相应的判决值，进而对该用户的行为类别进行判别。
    假设在所需的检测时间内记录该时间段内用户的命令流，记为R=(R1，R2，…,Rn)。其中，Ri为第i个独立的shell命令序列，n为shell命令记录的总量,此时的命令序列R中的值是按照时间顺序依次得到的。
    利用训练中的参数匹配方法，对于命令序列R进行操作，得到状态转移序列q=(q1，q2，…,qx)，其中，x为状态转移序列内状态的总数,qi代表R中按时间排序的第i 个状态。HMM检测流程如下：
    (1)根据训练数据R生成w个shell命令序列流S1,S2…,Sw，设定初始m:=1,j:=1,n:=0。
    (2)如果m≤r-l(1)+1，则将Seqmj与L(j)进行比较，
   
3 实验设计与结果分析
    在本文的实验中,利用其中4个用户userl、user2、user3、user4的数据进行实验，并设合法用户为user2，将余下的user1、user3、user4视为非法或未知用户。在该4个用户的数据记录中皆有超过15 000条命令行记录。对于正常用户，实验中将利用其中的前5 000条命令进行正常行为模式的训练，得到HMM观测值集合并确定HMM参数，后5 000条命令作为正常行为的检测。对于非法用户，将分别用其中的5 000条命令进行异常检测的测试。在HMM模型建立及训练阶段的参数设置为W=3，C={3，2，1}。在HMM模型建立过程中，从正常用户user2的前5 000个shell命令中得到C(1),C(2),C(3)所对应的命令序列个数如表2所示。

    参考文献[6]方法的异常检测结果如图1所示,上方曲线为合法用户user2的正常行为测试数据对应的判决值曲线，下方的3条曲线为非法用户的异常行为测试数据对应的判决值曲线(以下同)。

    改进的HMM方法得到的异常检测测试结果如图2所示。可以看出，相对于user2，三组非法用户的值更加靠近于3，表明权值为2 和1 的命令序列所表示的合法用户的正常行为模式在3个非法用户行为序列中较少出现，从图1、图2 中可以看出，改进的HMM方法使得正常行为和异常行为测试数据对应的判决值曲线具有良好的可分性。

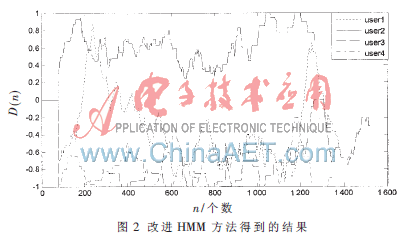
    参考文献[6]方法用于建模的命令序列有1 140个，而改进的HMM方法只有136个，大大节约了系统存储空间，所以，改进HMM的方法具有较好的检测准确度，本文在运算成本和计算效率之间取得了权衡，在实验中取得了一个很好的效果。
    本文提出一种基于隐马尔可夫模型的用户行为异常检测新方法，并通过实验对该方法的性能进行了测试。实验表明，该方法具有很高的检测准确率和较强的可操作性。但需要指出的是，该方法中的一些检测思想虽然适用于以系统调用为审计数据的程序行为异常检测，但具体的操作方式及检测性能还有待分析和验证。
参考文献
[1] FORREST S, HOFMEYR S A, SOMAYAJIA. A sense of  self for UNIX processes[C]. Proceedings of IEEE Symposium on Security and Privacy, Los Alamos, California,1996.
[2] LEE W, STOLFO S J. Data mining approaches for intrusion detection[C].Proceedings of the 7th US ENIX Security Symposium, San Antonio, Texas, 1998.
[3] WARRENDER C, FORREST S, PEARLMUTTER B. Detecting intrusions using system calls: alternative data models[C]. Proceedings of the IEEE Symposium on Security and Privacy, Oakland, CA, USA, 1999:133-145.
[4] LANE T. Machine learning techniques for the computer security domain of anomaly detection[D].Purdue University  2000.
[5] 周星, 彭勤科, 王静波. 基于两层隐马尔可夫模型的入侵检测方法[J].计算机应用研究, 2008,25(3):911-914.
[6] 邬书跃，田新广.基于隐马尔科夫模型的用户行为异常检测新方法[J].通信学报,2007,28(4):38-43.