摘  要： 研究了不同角度、不同阶数的基于Koch曲线的天线性能，仿真和测试结果表明，在保持天线长度不变的条件下，随着角度和阶数的增加，天线的谐振频率下降，而天线的方向图依然具有半波振子的低方向性。在此基础上，综合Koch和Hilbert曲线，设计了一款尺寸为55mm×10mm的小型化电子标签。该标签天线不仅具有半波阵子的低方向性，而且简单、便于调谐。 

    关键词： Koch曲线； Hilbert曲线； RFID； 电子标签； 天线

    “分形”是Benoit.B.Mandelbrot在1975年提出的^[1]，其原意是“不规则的、分数的、支离破碎”的物体。分形具有两个重要特征，即自相似性和标度不变性。“分形天线”一词是在1993年IEEE年会上出现的，在1995年8月Cochen发表了分形天线的第一篇论文^[2]。分形天线是指基于分形结构而设计的天线。分形结构的自相似特性和标度不变特性在分形天线的设计中体现为多频带特性和尺寸缩减特性。此外，分形天线和分形天线阵具有低的旁瓣电平^[3-5]。 

    传统的Koch曲线采用角度为60°的三角形加载，本文突破常规，在保持天线高度不变的条件下，研究了角度分别为30°、45°、60°、75°时，标签天线的性能，并研究了不同阶数时的天线性能。在此基础上，设计并制作了基于Koch和Hilbert联合加载的电子标签，该标签不仅具有较好的性能，而且简单、便携、便于应用。 

1 分形结构原理 

    在欧式空间中，人们习惯于整数维数，不会出现小数。而分形理论打破常规，把维数从整数推广到了分数。分形曲线的分数维是一个特征数，用来度量结构的不平度、复杂性、卷积度等，可以是小数。即物体或者集合图形的维数可以是连续变化的。对于具有自相似结构的分形图形，其维数D是下列方程的解： 

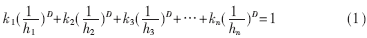
式中k_n为初始曲线的拷贝数，h_n为缩放比例，n为缩比尺度数。 

1.1 Koch曲线分形技术 

    Koch分形几何是在1904年被瑞典科学家Helgevon Koch提出的。Koch分形几何是由仿射变换集的迭代函数系统(IFS)生成。 

    Koch曲线因其具有很强的空间填充属性，因而近年来在实现天线小型化设计中受到广泛的重视和深入研究。由于Koch曲线的拷贝数为4，缩放比例为3，代入式(1)可以求得Koch曲线的分形维数为1.262，所以，它是介于一维和二维之间的图形。 

    Koch曲线的迭代过程如图1所示：将偶极子天线的两臂分为三等分，将中间的三分之一臂长换为两个等长且相交60°的线段，就得到1阶Koch曲线，依此类推可以得到高阶Koch曲线。这样不难知道，曲线的总长为L=h×(4/3)ⁿ, h为曲线的高度， n为分形阶数。其数学推导可以由仿射变换(IFS)得到^[6]。 

其中，a、b、c、d、e、f均为实数，a、b、c、d表示旋转和收缩，e、f表示位移。w为仿射变换。x₁，x₂分别为分段点处的坐标。将仿射变换写为: 

式中,W为Hutchinson算子，w为仿射变换，A为几何整体，m为拷贝数。 

    对于Koch曲线，拷贝数m为4，θ=0°，60°，-60°，0°，r=1/3,根据Koch的迭代原理，算出位移。根据参考文献[6]，Koch曲线的迭代如下所示。 

1.2 Hilbert曲线分形技术 

    Hilbert分形具有松散的自相似特性：0阶Hilbert是一个正方形轮廓的“半环”结构，设其边长为b、1阶是用0阶的结构来填充每条边，从而在每条边上形成“半环”结构，设其边长为a，将a/b称为Hilbert分形的比例系数，如图2示。 

    由图2可见，1，2，3，...，n阶Hilbert分形的轮廓面积与0阶的完全一致，即无论迭代多少次，Hilbert分形的轮廓面积保持不变，且始终只有2个端点。 

    分析可得，n阶Hilbert分形的总长度可由如下的（6）式算得。例如：n取0、1、2、3时，分别为：3b、5b、9b、17b。 

    Vinoy等人在参考文献[7][8]中详细探讨了Hilbert曲线在设计紧凑型谐振天线应用后发现，Hilbert分形天线的尺寸减小到λ/10时，性能却同λ/2偶极子相似。而Zhu在参考文献[9]中研究了馈点位置对Hilbert分形天线输入阻抗的影响，结果发现，无论迭代的次数多少，中心馈电的辐射电阻很小，但恰当地选择偏心馈电总能提供50 Ω的匹配阻抗。 

2 分析与研究 

2.1 阶数对天线性能的影响 

    基于Koch曲线的偶极子天线的不同阶数的模型如图3所示。天线的高度为120 mm，线宽为0.5 mm，角度为60°，铜箔厚度为0.015 mm。 

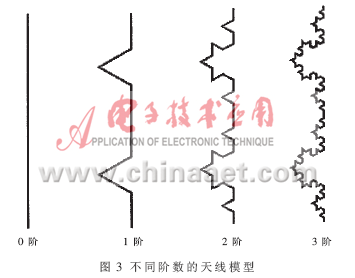
    利用基于FDTD算法的电磁仿真软件Ansoft HFSS 10.0进行仿真，仿真结果如图4所示。 

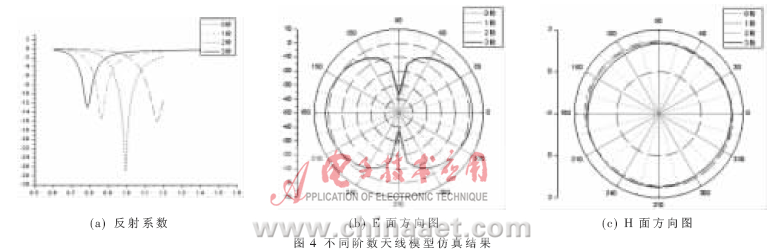
    从图4可以看到，对于0阶天线，其谐振在1.17 GHz，在保持天线高度不变的条件下，随着阶数的增加，天线的物理尺寸加长，从而使谐振频点下降，辐射电阻增大;尽管在不同的阶数对应不同的谐振频率，但是方向图依然具有普通偶极子的性质。需要说明的是，这里选择天线的高度不变，而不是选择天线线宽不变，这是因为，根据参考文献[10]的推导，天线的辐射功率因子与天线的有效体积成正比。由于辐射功率因子衡量的是辐射的实际功率和电抗功率之比，所以辐射功率因子越大越好，即要求天线的有效体积越大越好。惠勒对比了轴线型对称阵子和方环的有效体积，其结论是：虽然细导线和粗圆锥的实际尺寸大不相同，但是有效体积相差甚小。这是因为天线的有效体积受长度的影响较大，受横向尺寸影响较小所致。所以，这里的对比是以天线高度不变为条件的。 

2.2 角度对天线性能的影响 

    对于Koch曲线，传统的研究都是在角度为60°的条件下设计模型的。这里分别研究了角度为30°、45°、60°和75°的基于一阶Koch曲线的天线性能。根据以上的分析，这里依然选择天线高度为120 mm保持不变，线宽0.5 mm，铜箔厚度为0.015 mm。依此设定构造的模型如图5所示，仿真分析结果如图6所示。 

    图6的仿真结果表明，随着角度的增加，天线的谐振频率下降，但方向图不会受很大影响。不同的是天线的增益。因为当保持中间1/3长度不变时，不同的角度将分别构成底角为30°、45°、60°和75°的等腰三角形，由于角度的不同导致两腰的长度之和不同，这样，随着角度的增大，天线的物理尺寸就相应地增长，从而导致谐振频率下降。需要说明的是，当角度发生变化时，Koch曲线的拷贝数为4，但缩放比例不为3，因此，分形维数不再是1.262。 

3 设计与应用 

    基于以上分析，这里设计一款基于Koch曲线和Hilbert曲线联合加载的具有静电防护功能的电子标签。天线的尺寸为55 mm×10 mm，铜箔厚度为0.015 mm，天线蚀刻在0.05 mm的PET材料上。所选用的标签芯片在915 MHz，对外呈现的阻抗为Z=18.1-j149Ω。标签模型如图7所示。 

    尽管Koch曲线的高次迭代曲线可以实现预期的天线指标，高次迭代的曲线在理论上是可行的，但是，在实际应用中高次迭代的曲线结构复杂，受制作工艺水平的限制。所以，这里的天线两臂是采用Koch曲线加载，而短路环采用Hilbert曲线加载。这样设计的优点不仅达到了天线尺寸的缩减，而且Hilbert曲线构成的环状结构，不仅通过感性加载抵消芯片的容性，而且在直流状态下，对标签芯片构成短路，通过环状铜箔本身的电阻对静电放电，实现对标签芯片的静电保护。在仿真调试中发现，Hilbert环的高度对天线性能的影响比较大，而加载的位置对天线的性能影响比较小，从而可以通过改变Hilbert环的高度来对标签天线进行调谐。 

    从图8可以看到，在频率为900 MHz，天线的VSWR=1.13，增益为1.87 dB，从图8(c)可以看到，相对于普通偶极子，该天线的尺寸缩减了约60%，但是却具有普通偶极子的低方向性。用远望谷公司的XCRF-804阅读器，在功率为20 dBm(0.1W)时，测得阅读距离为2.5～3 m。目前该标签用于鞋厂对出厂产品的不开箱检测。 

    对于电子标签而言，由于标签天线作为标签芯片与阅读器实现通信的接口。因此，标签天线性能的好坏将决定RFID系统的灵敏度和阅读器读写的距离。标签天线设计的总体目标是设计结构紧凑，外形轮廓小巧，高增益，低副瓣。而分形天线工程是实现这一目标的方案之一。 

    本文研究了决定基于Koch曲线的标签天线性能的两个主要因素，即角度和阶数。通过仿真和调试发现，随着角度和阶数的增大，天线的谐振频率下降。这对天线的小型化设计提供了重要的指导。此外，基于实际应用的考虑，设计了一款基于Koch和Hilbert曲线联合加载的标签天线，不仅具有小的天线尺寸，较好的增益和带宽，而且结构简单，便于调谐，完全满足实际应用的需要。 

参考文献 

[1] MANDELBROT B B. The fractal geometry of nature[M].San Francisco: Freeman 1983. 

[2] 钱四林，施建超，黄华.分形理论在天线设计中的应用.山东通信技术，2007，6(2):33-37. 

[3] WERNER D H, GANGULY S. An overview of fractal antenna engineering research. IEEE Antennas Propagant.Mag.2003，45:38-57. 

[4] VIONY K J. Fractal shaped antenna elements for wide and multi-band wirless applications. Ph.D.dissertation, Dep.Elec.Eng.,Pennsylvania State University Park, 2002. 

[5] GIANVITTORIO G J. Fractal antennas: design,characterization and Applications. Ph.D.dissertation,Dep.Elec.Eng.,University of California at Los Angeles,LosAngeles,2000. 

[6] VINOY K J, JOSE  K A, VARAD V K. Resonant frequency of hilbert curve fractal antenna. IEEE International Symposium on Antennas and Propagation Digest,2001,3: 648-651. 

[7] ANGUERA J, PUENTE C, SOLER J. Miniature monopole antenna based on the fractal cureve, IEEE International Symposium on Antennas and Propagation Digest, 2002,4:546-549. 

[8] ZHU J, HOORFAR A, ENGHETA N. Feed point effects in hilbert curve antennas, IEEE International Symposium on Antennas and Propagation and USNC/URSI National Radio Science Meeting. 

[9] 阮成礼.超宽带天线理论与技术.哈尔滨:哈尔滨工业大学出版社,