摘 要: 局部嵌入分析(LEA)是图嵌入化的局部线性嵌入(LLE)方法。在头姿态估计问题上,选择局部邻域时只考虑属于同一类的姿态,但失去了相邻姿态的几何拓扑信息。为此,提出一种改进的邻域选择方法,充分利用先验姿态信息,使降维后的流形更加平滑,同类姿态互相靠近,不同类姿态之间的距离随着姿态差值变大而增大,且能够使训练及测试样本的低维流形更加靠近,降低了估计误差。在Facepix人脸数据库上的实验证明了该方法的有效性。
关键词: 头部姿态估计;流形学习;图嵌入;局部嵌入分析;局部线性嵌入
头部姿态估计是计算机视觉和图像模式识别领域中的一个重要研究课题,近年来受到了越来越多的关注[1]。在人脸识别中,如果得到的人脸图像是非正面的,识别的效果会大大降低,而如果预先估计人脸姿态后选择合适的视角模型进行识别,将会提高非正面人脸的识别率[2]。由于通过人脸的姿态可以得知人注视的方向,所以姿态估计在理解人的注意力等方面有很高的研究价值。
对于头部姿态估计问题,现有的方法大致可分为基于表观的方法和基于模型的方法两大类[3]。基于表现的方法是通过对含有各种姿态的人脸图像进行学习,建立一个能够估计姿态的分类器。这种方法对图像的分辨率要求不高,并且不需要或者需要较少的面部特征点,能够估计角度较大范围的姿态。基于模型的方法是利用某种几何模型来表示人脸的结构和形状,并通过提取某些特征,在模型和图像之间建立起对应关系。这种方法严重地依赖于特征点的定位结果,当图像旋转较大角度时,部分面部特征将丢失,无法进行估计,所以估计的姿态范围较小。
1 基于流形学习的头部姿态估计
基于流形学习的头部姿态估计属于表观类方法,它的基本思想是考虑每个高维头姿态图像都处于一个有姿态变化的连续流形中。目前已经吸引了一些学者对它进行研究,例如HU N等人[4]提出了通过对特定人的姿态流形的学习,在假定姿态流形不变的情况下,利用预测网络来估计其他人的图像的姿态的方法;FU Y[5]等使用了图嵌入GE(Graph Embedding)[6]结合流形学习算法进行人脸的姿态估计研究。
流形学习LLE[7](Locall Linear Embedding)算法是通过建立局部邻域权重图将数据由高维降至低维,但其邻域均采集自同一流形,对于姿态估计,这将导致姿态估计与人有关。FU Y[5]等人提出了一种改进的LLE即LEA(Locall Embed Analysis):利用数据集的已知类别信息选择局部邻域时,只考虑属于同一类(即同一姿态)的数据点,并结合图嵌入理论,使改进后的LLE近似线性。这样对于姿态估计将大大提高姿态估计的身份无关性。但这又带来一个新的问题:属于同一类的数据集映射到低维空间中后,退化成为一点,失去了几何拓扑信息,并且所有邻域均为同类样本(即不同人的相同姿态),这使得降维后的流形失去了其相邻姿态间的平滑性。
本文对FU Y等人提出的LEA方法做了进一步的改进:由于邻域的选择是流形学习算法至关重要的第一步,关系到邻域样本权值的计算及最后的降维结果。因此,本文在构造邻域时通过改进邻域距离表示方法,更好地选择邻域,使样本的邻域更好地重构样本本身,以解决LEA降维后的流形不能很好地保持高维时所具有的几何拓扑结构的不足,并使训练流形和测试流形更加靠近,减少姿态估计误差。



对于头部姿态估计问题,本文提出算法的流程为:
(1)训练姿态流形
①裁剪图片,使图片仅包含头部姿态部分,并对图片预处理、归一化,使所有图片有相同大小。
②提取特征作为训练特征(也可以不提取,直接用图片像素作为特征),并将特征用一个列向量来表示。
③根据式(6)计算样本点之间的距离,求出邻域矩阵,接着求解式(3),计算权值矩阵,然后求解式(5)计算投影矩阵P。
④应用Y=PTX,计算低维映射Y。
(2)测试样本姿态估计
①同训练步骤①,对测试图片进行裁剪、预处理、归一化等操作。
②应用投影矩阵P计算出测试样本的低维表示。
③应用KNN分类器估计测试样本姿态。
5 实验
5.1 人脸库
为了验证算法的有效性,本文在FacePix人脸姿态数据库上进行了实验。FacePix人脸库是2005年由CUbiC(the Center for Cognitive Ubiquitous Computing)、Arizona State University提供,该人脸库包含了不同姿态、不同光照的人脸,本文只介绍不同姿态的图片:具体为30人,每人181张不同姿态的人脸图像,姿态范围为水平方向上从-90°~90°(负的表示向左旋转),间隔为1°,共计5 430张分辨率为128×128的彩色人脸图像。本文将图片裁剪为32×32(人脸库中的第16、21、27三人由于图像采集不好,未被纳入实验中)大小的图片。人脸库样例及低维可视化流形如图1所示。

5.2 实验结果及分析
(1)低维可视化效果
图1(a)是FacePix人脸库经裁剪后的部分样例图,按照每行为同一人,每列为同一姿态排列,姿态从左到右分别为-90°、-60°、-30°、0°、30°、60°、90°;图1(b)是FacePix人脸库中第一个人的181张姿态图像经本文改进的LEA算法降维后的三维嵌入流形,嵌入流形的图片姿态按照-90°、-60°、-30°、0°、30°、60°、90°排列,邻域K=80,特征为裁剪并处理后的灰度图。由图1(b)可以看出,不同姿态处在低维不同位置,且按照姿态顺序呈流形分布。
(2)头部姿态实验
训练及测试样本三维流形如图2所示,图2实验选取的特征均为裁剪并处理后的灰度图。图2(a)为LEA算法的低维嵌入图,邻域k=8,图中颜色较深的线为人脸库中前9个人的流形,为训练流形;颜色较浅的线为中间9个人应用训练出的投影矩阵P投影后的结果,为测试流形。图2(b)为本文改进后的算法的嵌入图,邻域k=13,图中不同颜色的含义同图2(a)。通过图中效果比对可以看出,改进后的算法更能使测试样本和训练样本的相同姿态靠近,利于分类误差的降低。

对LEA算法和改进后的算法做相同条件下的对比试验。分别选取FacePix人脸库中前9人、前12人、前15人、前18人做训练样本,对应的后18人、后15人、后12人、后9人做测试样本,每人181张图片。由于改进后的算法仍是基于LLE算法的,所以邻域、嵌入维数以及参与训练的图片数对实验效果均有一定影响。实验中的特征均为裁剪并处理后的灰度图。表1为实验的姿态估计平均误差表。
图3中实验为:低维维度m=14,训练样本为9个人1 629张图片,测试样本为18个人3 258张图片,LEA算法邻域取k=8,改进算法邻域取k=10。图中实线为LEA算法姿态估计误差,其平均误差为3.44°;虚线为改进算法姿态估计误差,其平均误差为2.99°(如表1所示)。
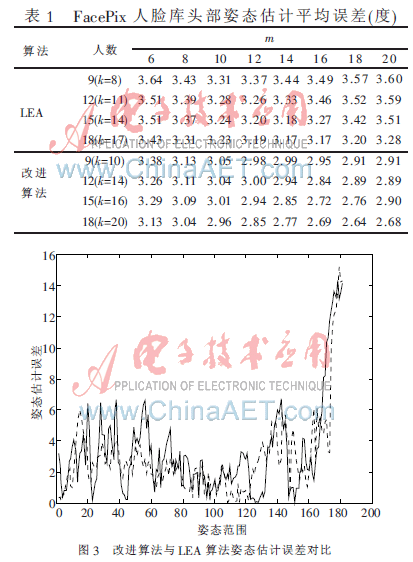
从表1及图3可以看出,改进后的算法与原来的算法相比,其误差降低不少。主要原因:如图2所示,由于LEA算法的邻域取自同姿态样本,其缺点是降维后同类样本重合在一起,理论上是类间距离越小越好。但是由于人的差异性,同样的姿态不同的人会有差距,所以导致训练出的流形与测试样本的流形有很大差距。改进算法由于适当扩大邻域,既包括同类样本又包括姿态相近的样本,这样训练流形与测试流形的差距就会缩小。
本文提出了一种对局部嵌入分析(LEA)算法改进的头部姿态估计方法(即一种新的邻域选择方法),在邻域选择时充分利用先验姿态信息,使降维后流形更加符合高维时的姿态间的几何关系,降低姿态估计误差。由实验可知,本文对LEA算法改进的有效性。然而由于流形学习算法的实验结果与参数(如邻域k、降维维度m等)有很大有关,并且数据库由于图像裁剪不同,实验效果也不尽相同,因此算法还有待进一步的研究与探讨。
参考文献
[1] CHUTORIAN E M, TRIVEDI M M. Head pose estimation in computer vision: a survey[J]. IEEE transactions on Pattern Analysis and Machine Intelligence, 2009,31(4):607-626.
[2] LI S Z, FU Q D. Kernal machine based learning for multi-view face detection and pose estimation[C]. Proceedings of 8th IEEE International Conference on Computer Vision. Vancouver, Canada: 2001.
[3] 马丙鹏. 基于表观的人脸姿态估计问题研究[M].北京:中国科学院,2009.
[4] HU N, HUANG W, RANGANATH S. Head pose estimation by non-linear embedding and mapping[C]. Proceeding. IEEE International Conference on Image Processing. 2005.
[5] FU Y, HUANG T S. Graph embedded analysis for head pose estimation[C]. Proceeding. IEEE International Conference on Automatic Face and Gesture Recognition. 2006.
[6] YAN S, XU D, ZHANG B, et al. Graph embedding: a general framework for dimensionality reduction[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2005.
[7] ROWEIS S,SAUL L. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000,290:2323-2326.

