边缘是指局部强度变化最显著部分.主要存在于目标与目标、目标与背景、区域与区域之间,是图像分割、纹理特征和形状特征等图像分析的重要基础。如何快速、准确提取图像的边缘信息一直是国内外研究的热点,目前已有多种边缘检测算法,其中最经典的算法就是Sobel算法。该算法由于计算量小、速度快,广泛应用于诸多领域,但其检测方向有限,抗噪能力较低,因此,该算法也具有一定的局限性。而且,实际应用中,像素级已无法满足精度要求,只能采用亚像素级的细分算法。
这里给出扩展的4个方向的Sobel算子,即采用4个方向的模板,细化处理其梯度方向图,鉴于插值法计算量小、精度高的特点,故选用二次多项式插值法实现亚像素细分。
2 扩展的Sobel细化算子
2.1 扩展的两个模板
图像目标的边缘是灰度不连续性的反映,其种类可粗略区分为:阶跃性边缘和层顶状边缘。前者的两边像素点灰度值显著不同,后者位于灰度值从增加到减少的变化转折点。为了更准确描述图像边缘点.减少噪声对其检测结果的影响,提高算子的抗噪能力,在水平、垂直模板的基础上重新构造2个3x3的模板,模板各个位置的权重是由该位置到中心点的距离以及该位置在模板中所在的方向决定的,等距离的点具有相同权重,如图l所示。这里选用最高输出模板所对应的边缘梯度值作为像元边缘梯度强度。
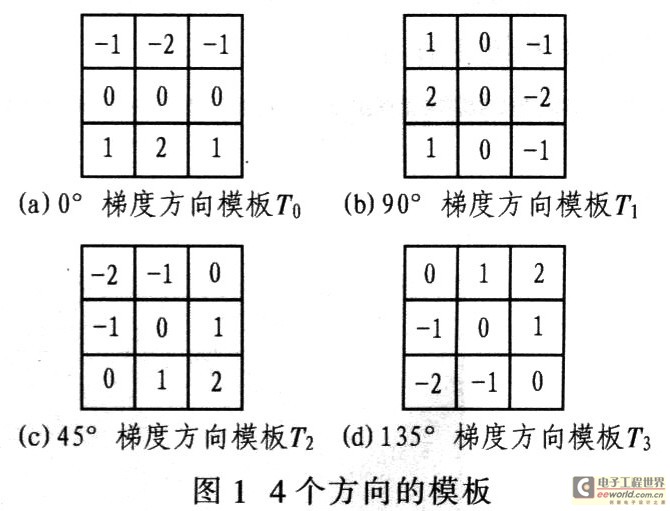
2.2 Sobel算子细化边缘
图像边缘包含图像的大量信息,但模板计算的数值仅仅只是图像对应的梯度图像,边缘出现于梯度较大位置,若想提取图像边缘必须设定阈值将其二值化。由一阶梯度算子得到梯度图像,一般边缘较粗,若直接对其梯度图像设定阈值进行二值化,很难找到合适的阈值.也不便于边缘连接与边缘特征提取等后期处理。因此在对图像梯度图像进行二值化前,必须细化所检测的梯度边缘。细化原理是基于经典Sobel算子定义的:
![]()
梯度方向为:

Sobel算子模板中的元素表示算式中相应像素的权重因子。Sobel算子是边缘检测算子,故其处理模板中各因子之和为零。另一方面,由于正因子和负因子之和分别为4和一4,在极端情况下处理结果可能溢出。因此,在实际使用时,Sobel算子通常采用已设定阈值进行二值化,即处理结果得到的是已二值化的边缘图。该结果将导致边缘图中幅值较小的边缘丢失。为了克服这个缺陷,引入一个衰减因子Scale,用它去除计算结果,来消除数据的溢出,而无需二值化处理,而且其结果是无失真的灰阶边缘图,从而保留所有边缘数值同。加入扩展的模板后可得:

因子Scale取4,它也是归一化因子,即两个灰度层的阶跃,交界处的处理结果就是其灰度差值。
灰度图像细化处理步骤如下:①对灰度图像作带衰减因子的Sobel处理,得灰度边缘图。Sobel处理采用式(3);②对所得灰度边缘图再作带衰减因子的Sobel处理;③灰度边缘图减去Sobel处理结果,再将与负值部分对应的边缘点的值改为零,得到细化的边缘图。
3 多项式插值亚像素细分的精定位
运用Sobel细化算子改进的方向模板获取边缘点的梯度方向,可采用已知的边缘点的梯度方向近似代替未知的亚像素点的梯度方向,并在该方向上进行二次多项式插值得到边缘的亚像素位置。
对于灰度图像中任意点的梯度幅值用R表示,设R0为边缘点P0(m,n)的灰度梯度方向的模,R-1,R1分别是在梯度方向上与P0相邻的两像素点P-1,P1的梯度幅值,经推导可得亚像素点的坐标(xe,ye)为:
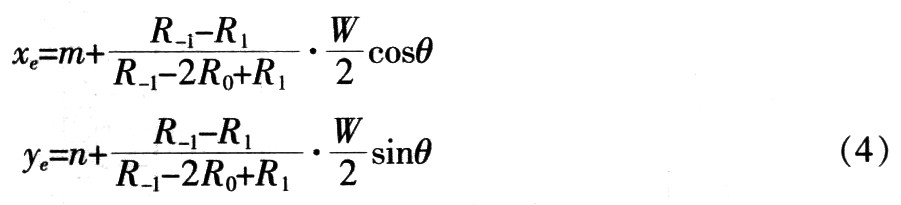
式中:W为相邻像素点到边缘点距离,θ为梯度方向与x轴正向夹角。
由式(4)可得出,亚像素细分定位边缘的前提条件为:R0>R-1且R0>R1。
采用扩展的Sobel细化算子搜索单像素边缘,在搜索过程中,剔除边缘点梯度方向的非极大值,从而保证亚像像素细分定位的前提条件成立。方向模板与P-1,P1点坐标对应表如表1所示。

4 实验与结果分析
为了验证该算法,提取在线实时采集的微小零件图像进行实验。
(1)可扩展的Sobel细化算子的验证 引入灰阶Sobel算子后,得到的边缘图仍是灰阶图像,此时采用Sobel算子处理,得到边缘的边缘图。在新的边缘图上,原边缘的两侧得到新的边缘,而中间部分却变成背景,且其宽度小于原边缘。利用该特点细化原边缘,即将原边缘减去新边缘图,再将结果中与负的部分对应的边缘变为零,最后得到接近单像素宽的边缘图,从而达到细化边缘的效果,如图2所示。

(2)亚像素细分算法定位 经过扩展方向模板的Sobel细化算子后,提取接近单像素的边缘,在其梯度方向上用亚像素细分算法对图像边缘进一步定位。
图3是在原边缘基础上取一段圆弧,对其细分前后的坐标图,可以看出,经过亚像素细分算法定位后得到的像素边缘比较光滑。相对于未细分,其精确度得到提高。
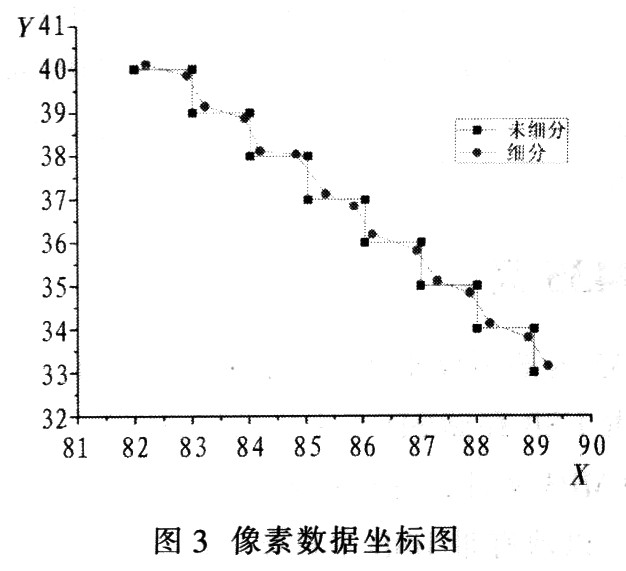
(3)计算标准偏差 以单个点的像素坐标值为标准坐标值,将定位后的单点与对应点的坐标差作为算法偏差,计算得到的标准偏差约0.20 pixel。
5 结论
采用的边缘检测算法是通过扩展的4个方向的Sobel算子引入衰减因子而得到无失真的灰阶边缘图,再采用Sobel算子细化,可使较陡边缘部分光滑连续,且接近单点宽的边缘;采用二次多项式插值法在梯度方向插值后得到光滑边缘,定位精度达到0.20 pixel,适于对精度要求较高的视觉系统。

