摘  要： 提出了一种基于离散小波变换、混沌系统和二维经验模式分解的彩色图像数字水印算法。首先，对彩色载体图像的G通道进行一级小波分解，将其低频分量进行混沌位置置乱；然后将置乱后的低频分量进行二维经验模式分解，分解成5个基本模式分量和1个残差分量；最后，用水印信息代替第4个中低频基本模式分量实现信息嵌入。利用归一化互相关函数和峰值信噪比对算法进行评定，并对含水印的图像进行攻击。实验结果表明，该算法嵌入容量较大，且具有较好的透明性和鲁棒性。
关键词： 数字水印；混沌系统；二维经验模式分解；离散小波变换

　数字图像水印发展非常迅速，数字图像数据的版权保护也显得越来越重要。通过在数字图像载体中嵌入水印，可以实现盗版确认、使用跟踪等功能。以数字图像为载体的经典的信息隐藏算法基本可以分为两类：时域算法和变换域算法。时域算法的主要代表有LSB算法[1]，其算法比较简单、容量大，但是鲁棒性差。目前，变换域算法由于对视觉影响小，鲁棒性好而受到研究者的重视。研究的方向主要集中在DCT变换[2-3]、DFT变换域[4-5]、DWT变换[6-7]及其他正交域[8]。虽然变换域算法的鲁棒性普遍比空域算法好，但变换域的算法容量普遍较小，无法和空域算法容量相比。参考文献[9]提出了一种基于BEMD(Bidimensional Empirical Mode Decomposition)分解[10]的数字水印算法，该算法达到了空域LSB算法容量水平，并对椒盐噪声、缩放、小波变换实现的压缩有一定的抵抗能力，但其基本不具有抗JPEG压缩攻击的能力。另外，由于BEMD分解的系数取值空间有限，进而使其密钥空间很小，导致该水印算法的安全性不高。
　针对参考文献[9]算法的不足，本文以彩色图像G通道信号为载体，利用HVS系统对绿色的不敏感性，提高算法的不可感知性；利用DWT变换鲁棒性的优点，提高算法的鲁棒性；利用混沌系统对初值的敏感性，提高算法的安全性[11]；利用二维混沌置乱的高效性，提高BEMD分解的有效性，同时置乱增加了图像分解后中低频幅度频谱强度，提高了算法抗JPEG压缩攻击的能力[12]。实验结果表明，本文提出的改进算法容量依然很大，可达到空域LSB算法四分之一的水平，显著增强了其抗JPEG压缩攻击能力，同时提高了算法的安全性。
1 混沌序列
　混沌现象是在非线性动力系统中出现的确定性的、类似随机的过程。这种过程既非周期，又不收敛，并且对初始值有极其敏感的依赖性。
　一个一维离散时间非线性动力系统定义如下：

2 二维经验模式分解
　HUANG N E提出将原始信号分解为一些不同IMF(Intrinsic Mode Functions)分量之和，并对分解后得到的IMF分量进行Hilbert变换，获得分量的瞬时频率和振幅，即Hilbert谱[14]。物理上定义一个有意义的瞬时频率所需要的条件是具有局部均值为零的对称性，并且具有相同的零交叉和极值数目。因此，HUANG N E给出的IMF定义满足以下两个条件：
　(1)在整个信号数据段内，极值点的个数和过零点的个数必须相等或最多相差一个。
　(2)在任何一点，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的均值为0。
　EMD分解基于如下假设：
　(1)信号至少有两个极值，即一个极大值和一个极小值。
　(2)信号特征时间尺度由两个极值之间的时域信号的下降沿定义。
　(3)当整个数据序列没有极值点而只有拐点时，能够在进行一阶或几阶运算后重建极值点。
　几乎所有的信号都是非线性、非稳态的，它们不满足构成IMF的条件。因此，需要采用筛选算法，将复杂信号分解为若干个IMF之和。
　对于一个二维m×n图像信号f(x，y)，x=1，2，…，m；y=1，2，…，n。BEMD分解[4]的实现过程如下：
　(1)外部初始化，令待处理的图像为：
　　r0=f(x，y)，j=1
　(2)筛分抽取第j个IMF：

　
　
5 实验结果
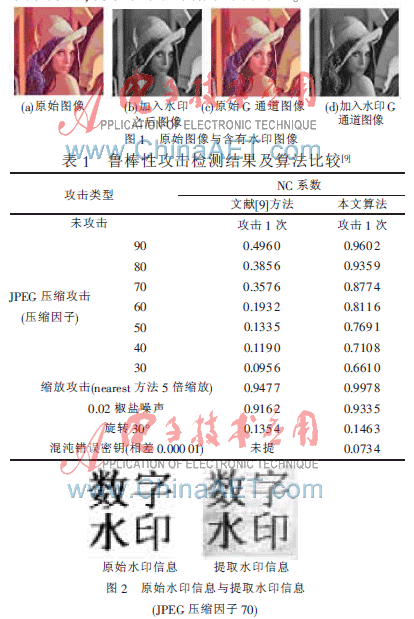
　实验采用Lena(256×256)彩色图像作为原图像，原水印信息为128×128的二值图像。结果表明，这种算法的不可见性很好，如图1所示。实验计算得峰值信噪比PSNR=34.540 5 dB，也说明算法的透明性很好。算法抗攻击的测结果如表1所示，图2所示的是JPEG压缩因子为70时，提取水印和原始水印的对比。

　本文提出基于小波变换(DWT)、混沌映射和BEMD分解数字水印算法，首先根据HVS系统对绿色敏感度低的特点以及小波变换抗压缩攻击的特点，使用小波基将原始彩色载体图像的G通道图像信号整体进行一级小波分解。然后为了提高算法的安全性和中频分量的强度，对原始G通道图像信号小波分解得到的近似分量，进行Logistic二维混沌位置置乱，再对置乱后得到的近似分量进行BEMD分解。为了提高抗算法的鲁棒性，选取替换中低频的IMF分量进行水印嵌入，充分利用了图像的冗余空间，使鲁棒性和不可感知性达到了比较好的平衡。实验表明，该算法容量大，当载体图像为256×256时，嵌入的容量为128×128 bit参考信息。同时该算法能够抵抗噪声、缩放、JPEG压缩的攻击，与参考文献[9]算法相比，本文算法的抗JPEG压缩攻击的鲁棒性有了明显的提高。然而这种信息算法还存在两个问题：一是不能抵抗旋转攻击和剪切攻击；二是算法是非盲的，即水印提取时需要原始载体图像。如何解决这些问题将是下一步算法改进研究的重点。
参考文献
[1] VAN S R， GTIRKEL A， Z’OSBORNE C F. A digital watermark[C]. IEEE International Conference on Image Processing  Austin Texax USA， 1994：86-90.
[2] COX I J. Secure spread spectrum watermarking for multimedia[J]. IEEE Transaction on Image Processing，1997， 6(12)： 1673-1687.
[3] 黄继武，SHI Y Q，程卫东. DCT域图像水印：嵌入对策和算法[J].电子学报，2000，28(4)： 57-60.
[4] SOLACHIDIS V， PITASI. Circularly symmetric watermark embedding in 2D DFT domain[J].IEEE Transaction on Image Proeessing，2001，10(11)： 1741-1753.
[5] 王向阳，邬俊，侯丽敏.一种基于图像特征点的数字水印嵌入方法[J].电子学报，2007，35(7)：1318-1322.
[6] 柏森，胡中豫，吴乐华，等.通信信息隐匿技术[M].北京：国防工业出版社，2005.
[7] 李智，陈孝威.小波和余弦变换相结合的灰度图像水印算法[J].中国图象图形学报，2006，11(6)：834-839.
[8] FALKOWSKI B J. Multi-polarity complex Hadamard transforms forphase watermarking algorithm[C].2007 6th International Conferenceon Information Communications & Signal Processing，2007：1-5.
[9] 张学敏，平子良，赵志芳. 基于经验模式分解的信息隐藏研究[J].内蒙古师范大学学报(自然科学汉文版)， 2010，39(3)：252-256.
[10] NUNES J C， BOUAOUNE Y， DELECHELLE E， et al. Image analysis by bidimensional empirical mode decomposition[J]. Image Vis Comput(S0262-8856)，2003，21：1019-1026.
[11] 陈巧琳，廖晓峰，陈勇，等.改进的基于混沌序列的幻方变换图像加密[J].计算机工程与应用，2005，22(5)：138-139.
[12] 谢建全，阳春华，黄大足，等.一种大容量的DCT域信息隐藏算法[J].中国图像图形学报，2009，14(8)：1542-1546.
[13] 易开祥，孙鑫，石教英.一种基于混沌序列的图象加密算法[J].计算机辅助设计与图形学学报，2000，12(9)： 672-676.
[14] HUANG N， ZHENG S， LONG S， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proccess Royal Society Lond， 1998， A454：903-995.