基于系统辨识的神经网络鲁棒性研究
2009-06-02
作者:江芳泽 黄晓东 李 昕 张永鑫
摘 要: 给出了神经网络鲁棒性的概念,基于系统辨识的BP网络、RBF网络和Elman网络的鲁棒性问题进行了分析和研究。仿真结果表明,神经网络用于非线性系统辨识有其广阔的前景。
关键词: 鲁棒性 神经网络 系统辨识
在控制系统的研究中,人们关心的最基本的问题是系统的稳定性在参数变化下保持的可能性。Davison在提出干扰不变性的内模原理时提出了系统结构稳定性的概念,这是一种基于无穷小扰动分析的鲁棒性概念。在实际系统中参数既不能视为不变,也不能仅具有无穷小扰动。系统工作环境的变化,模型的不精确性、降阶近似、非线性的线性化等都可化成一种参数扰动。有时系统受控对象可能有几个不同的工作状态。当用同一控制器来控制时,人们也把不同工作状态所对应的参数差别视为一种扰动,这种参数的变化只能被视为有界扰动。现代鲁棒性分析的最重要的特点就是要求讨论在有界扰动下系统性能保持的能力。
常系数线性系统鲁棒分析与氯控制正取得丰富的成果,但非线性系统的鲁棒性研究还是十分必要的。神经网络的非线性系统变换为非线性系统尤其是工业过程系统的辨识与控制提供了有效的途径。本文针对三种用于工业过程控制的典型神经网络(BP、Elman、RBF网络)算法的鲁棒性,进行了分析、比较和研究,最后给出了仿真结果。
1 三种神经网络的鲁棒性分析
有的文献将神经网络的鲁棒性与泛化能力混为一谈,比如将采用双BP算法,使网络输入值变化很小时,网络输出值基本不变看成是网络的泛化性。所以首先要明确什么是神经网络的鲁棒性。对于前向无反馈神经网络而言,神经网络的鲁棒性是指当输入信息或神经网络发生有限摄动时,神经网络仍能保持正常的输入—输出关系的特性;对于反馈神经网络而言,神经网络的鲁棒性是指当输入信息或神经网络发生有限摄动时,神经网络仍能保持稳定的输入—输出关系的特性。
神经网络的鲁棒性依赖于神经网络参数位置和它附近系统误差曲面的具体形态。神经网络参数设计在极值点附近而其附近的形态误差曲面又比较平缓时,网络的鲁棒性就好,否则鲁棒性就差。使系统误差曲面在设计处平缓的主要方法是选用平滑的变换函数,但平滑的变换函数又不利于提高网络的学习速度。BP网络、Elman网络、RBF网络的变换函数都是平滑的,所以问题的关键就是网络参数能否在极值点附近。
下面通过一个动态系统的实例进行分析。
动态系统的函数映射关系式为:
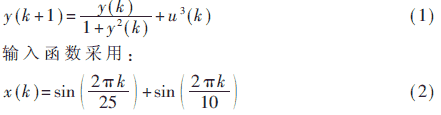
图1给出了系统的输入—输出延迟—输出的三维图,把输入和输出延迟都作为自变量时,就为利用静态网络辨识静态系统提供了可能性。
该动态系统的函数映射关系实际是基于NARMA模型的函数形式,因此可以把系统输入、输出和它们的延迟值同时作为静态神经网络的输入,从而使得静态神经网络能映射NARMA模型类的动态系统。NARMA模型是一种统一的有限可实现非线性系统的表达式。
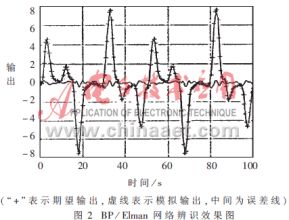
图2、图3分别为BP/Elman、RBF网络辨识系统的效果图。
2 仿真结果
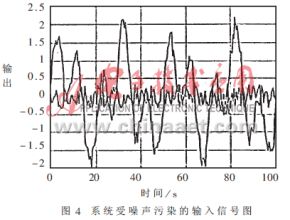
在上述所研究的系统中的输入上附加一随机量,如图4所示。它类似于工业过程中的噪声污染。
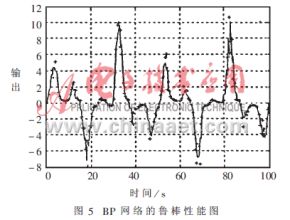
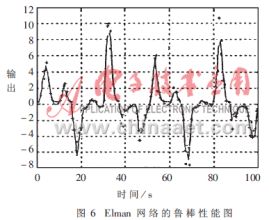
通过训练好的神经网络来模拟输出,并与系统的实际输出比较。从图5、图6、图7中可明显看出BP网络、Elman网络的模拟输出比较光滑,没有出现大的跃变,且与实际输出差值不大,而RBF网络与前者的最大差别是会出现大幅度的跃变。这是由于噪声的影响,受噪声污染的输入偏离了训练样本集中的输入,从而偏离了径向基函数的中心,这样其输出与真实值相差就很大。
从仿真结果中可知:RBF网络的最大优点是收敛速度快、逼近精度高、训练结果唯一;而最大的不足是泛化性能较差,所以当其输入偏离训练样本集时,系统表现出的鲁棒性就会很差。但它在时变快、学习样本集可基本覆盖整个系统的状态的情况下具有明显的优越性。所以针对系统的辨识与控制研究神经网络的鲁棒性是非常必要的。
参考文献
1 黄 琳,王 龙,于年才.系统鲁棒性的若干问题——背景、现状与挑战.控制理论及应用,1991;8(1):11~12
2 张邦礼,李银国,曹长修.非线性系统神经网络辨识的鲁棒BP算法.控制与决策,1996;11(1):26~27