一种改进的LMS/F组合算法及其在同址干扰抵消中的应用
2009-06-09
作者：袁小刚1， 黄国策1， 许 彬2
摘 要： 在研究最小均方算法LMS(Least Mean Squre)、最小四阶算法LMF(Least Mean Fourth)和LMS/F组合算法的基础上，引入修正因子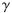
对LMS/F组合算法进行改进。改进的LMS/F组合算法在保持LMS/F组合算法优良的收敛精度和稳定性的基础上，进一步提高了收敛速度和对时变系统的跟踪特性。改进的算法参数调整简单、高效且运算量小，仿真结果与理论分析相一致，证实了该算法的优异性能。
关键词： 自适应滤波； LMS/F组合算法; 修正因子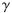; 干扰抵消
自适应数字滤波器自从20世纪60年代出现后，其理论不断地发展与完善，应用也越来越广泛。基于最陡下降法的LMS算法因其算法简单、稳定性好、可在线计算和易于硬件实现等优点而被广泛用于自适应控制、信道均衡、系统辨识及干扰抵消等领域；LMS算法的缺点在于其收敛速度和稳态误差性能无法同时得到满足，在确定步长时需要在收敛速度和稳态误差之间折衷考虑[1]。为解决这一矛盾，人们提出了许多变步长LMS算法，但其通常都是在增加较大计算量的前提下提高其收敛速度和稳态误差性能[2-4]。WALACH.E和WIDROW.B提出的LMF算法，在权值向量距离最优解较远时可以获得比LMS算法更快的收敛速度和更小的均方误差；但是在权值向量接近最优解时，其收敛速度和稳态误差性能均不如LMS算法[5-7]。LIM S J和JARRIS J G在综合LMS算法和LMF算法优点的基础上，提出了LMS/F组合算法。LMS/F组合算法在权值向量距离最优值较远时，收敛速度和稳定性比基本LMS算法好；在权值向量接近最优解时，稳定性比LMF算法好[4,8]。
衡量自适应滤波算法性能的指标有4个[1,9]：收敛速度、收敛精度、计算复杂度和对时变系统的跟踪能力。本文引入修正因子
对LMS/F组合算法进行改进，改进的算法具备更快的收敛速度、参数调整简单、高效且运算量小，能同时体现以上4个特点。
1 LMS算法、LMF算法和LMS/F组合算法
自适应滤波器由参数可调的数字滤波器和自适应算法两部分组成，其原理如图1所示。
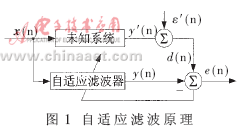
图1中，x(n)为n时刻输入信号矢量；d(n)表示n时刻的参考信号值或期望响应的信号值；w(n)为自适应数字滤波器的权值向量；e(n)为误差信号，可由公式(1)得到。
输入信号x(n)通过参数可调数字滤波器后产生输出信号y(n)，将其与参考信号(或期望响应)d(n)进行比较，形成误差信号e(n)。权值向量w(n)由误差信号e(n)控制，输出根据e(n)值而自动调整，使之适合下一时刻输入x(n+1)，以便使y(n+1)接近于所期望的参考信号d(n+1)。
1.1 LMS算法
LMS自适应滤波算法的独立性理论最早由Windrow和Huff提出，LMS算法权值向量的更新公式为[1]:
(2)式中步长μ为控制收敛速度的常数，e(n)为误差信号，x(n)为输入信号矢量。为了保证迭代后收敛，步长μ必须满足：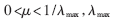
为输入序列x(n)自相关矩阵的最大特征值。
LMS算法具有算法简单、计算量小、易于实现、鲁棒性好和可在线计算等优点，在自适应滤波器的设计中得到了广泛应用，但其存在收敛速度和稳态误差性能无法同时得到满足的缺点。
1.2 LMF算法
WALACH E和WIDROW B 提出的LMF算法采用四阶误差信号最小化准则，在权值更新向量距离最优值较远时，LMF算法可以获得比LMS算法更快的收敛速度和更小的均方误差，其权值向量更新公式为[5]:
由于LMF算法在权值向量更新中采用误差e(n)的三阶函数，因而对附加噪声和信噪比都非常敏感。当信噪比较小、权值向量与最优权值向量误差较大时，可以获得较快的收敛速度和较小的稳态误差；但当信噪比变大时，LMF算法的性能将会急剧退化，并导致稳态性变差；在权值更新向量接近最优解时，其稳态误差的性能不如LMS算法。
1.3 LMS/F组合算法
LIM S J和JARRIS J G提出的LMS/F组合算法的权值向量更新公式如下式所示[8]：
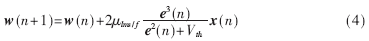
正数Vth是一个为保证算法快速收敛和较高收敛精度而设置的参数。e(n)>>Vth时，步长μlms/f趋近LMS算法步长μlms；e(n)<
LMS/F组合算法在计算量增加不多的基础上却同时兼有LMS和LMF算法的优点：在权值更新向量距离最优值较远时，收敛速度和稳定性比基本LMS算法好；在权值更新向量接近最优解时，稳定性比LMF算法好。LMS/F组合算法通过适当地设置μlms/f，Vth的改变不会引起收敛过程的振荡。当信号受加性高斯白噪声影响时，预设μlms/f≈2.2 μlms和Vth=5E[e2(n)]，LMS/F组合算法可以取得比较理想的收敛效果[4,9]。
2 改进的LMS/F组合算法
本文对LMS/F组合算法加入一个修正因子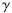
，提出一种改进的LMS/F组合算法，其权值向量更新公式如下
其中，修正因子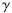≥1(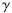≥1时即为基本LMS/F组合算法)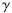，的具体取值将在下一节权值收敛条件中进行分析。
由(5)式可以看出在算法初始状态e(n)较大时，改进的LMS/F组合算法滤波准则的代价函数可由公式(6)表示、权值向量w(n)的更新公式可由公式(7)来近似。
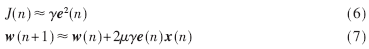
由公式(7)可以看出，改进的LMS/F组合算法权值向量的更新公式与LMS算法相近，且其步长为LMS算法的γ倍，则在当e(n)较大时可以保持较大的步长调整从而提高收敛速度。
在自适应算法收敛后到达稳定状态e(n)较小时，相比于Vth，可以认为e2(n)/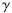≈0。则改进的LMS/F组合算法滤波准则的代价函数可由公式(8)表示、权值向量w(n)的更新公式可由公式(9)来近似。
因而在当e(n)较小时，其滤波准则与LMS/F组合算法相同，同时由公式(9)可知，其步长调整不受修正因子γ的影响，改进的算法可以保持较小步长，能够保证与LMS/F组合算法相同的收敛精度，相比于LMS算法可以得到更高的收敛精度。
3 改进的LMS/F组合算法性能分析
3.1 算法计算复杂度分析
本文提出的算法是基于LMS/F组合算法进行改进的，由公式(5)可以看出改进的算法参数调整简单高效。改进的LMS/F组合算法每次迭代时只需在LMS/F组合算法的基础上对修正因子γ多进行一次除法运算，因而其计算量增加很少。相对于基本LMS算法，每次迭代时仅仅增加了3次乘法、2次除法和1次加法，且不存在运算量较大的指数运算等因素。因而相比大多数的变步长LMS算法，该算法具有参数调整简单高效、运算量小的优点。
3.2 权值向量的收敛条件
为分析改进的LMS/F组合算法权值向量的收敛条件，把公式(5)写成变步长LMS算法形式：
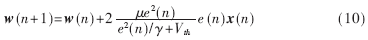
从公式(10)中可以得到该算法的步长因子,记为μ(n)。LMS算法的收敛条件为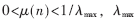
为输入序列x(n)自相关矩阵的最大特征值。则改进的LMS/F组合算法收敛条件为：
3.3 算法收敛性能分析
上一节已经分析了在自适应初始阶段e(n)较大时，可以保持较大的步长调整从而提高收敛速度；在算法达到稳态e(n)较小时，可以保持较小的步长调整从而能够保证较高的收敛精度。下面从步长μ(n)与误差e(n)的函数关系入手，进一步分析该算法的收敛性能。步长μ(n)与误差e(n)的函数关系曲线如图2所示。
图2显示了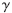
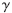=4、=2和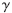=1时μ(n)和e(n)的非线性关系(其中，当时即为基本LMS/F组合算法)。由图2可以看出,当e(n)较大时，改进的LMS/F组合算法可以得到比LMS/F组合算法更大的步长调整，因而可以得到更快的收敛速度(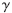的取值需满足公式(13)所给出的收敛条件)。当算法接近于稳态、e(n)较小时，改进的LMS/F组合算法的步长μ(n)与误差e(n)的函数关系曲线与基本LMS/F组合算法相一致，从而可以获得相比于LMS算法更高的收敛精度。
3.4 算法失调分析
在自适应滤波器中，失调δ是衡量其滤波性能的一个技术指标，用来描述自适应算法的稳态均方误差ξ对最小均方误差ξmin的相对偏移，即：
由(17)式可以看出，算法进入稳态后，算法的步长因子趋于极小，且远小于LMS算法，因而改进的算法的失调系数也极小，其性能优于LMS算法,与基本LMS/F组合算法保持一致。
3.5 计算机仿真结果
下面通过计算机模拟对改进的LMS/F组合算法进行仿真，并将其与LMS算法、LMF算法和基本LMS/F组合算法的性能进行比较，来检验改进的LMS/F组合算法的性能。计算机模拟条件如下:自适应滤波器阶数L=4，未知系统初始权值向量为w=[0,0]；参考输入信号是零均值、方差为1的高斯白噪声；ε(n)为与x(n)不相关的零均值高斯白噪声，方差为0.01。仿真中Vth=0.05，改进的LMS/F组合算法中修正因子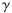
=4。分别做100次独立仿真，求其统计平均，得到的收敛曲线如图3所示。
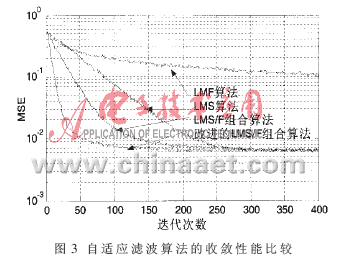
图3显示了LMS算法、LMF算法、LMS/F组合算法和改进的LMS/F组合算法的收敛过程和所能达到的MSE的情况。LMF算法的收敛速度较慢，在400次迭代之后还没有达到稳态。改进的LMS/F组合算法收敛速度最快，在收敛速度性能上的优势非常明显,其收敛精度与基本LMS/F组合算法一致，略优于LMS算法，因而可以获得很好的稳态误差性能。
4 改进的LMS/F组合算法在自适应跳频同址干扰抵消中的应用
自适应干扰抵消是指以噪声干扰为处理对象，将它们抑制掉或者进行非常大的衰减，以提高信号传输和接收的质量。自适应同址干扰抵消主要用于解决布置在同一平台(如车载、舰载或机载)收发信机间的干扰隔离问题。由于同址环境中发射机和邻近接收机的收发电平相差很大(最高可达50 dB～100 dB)，受收发信机天线的隔离度的限制，本地跳频电台发射机产生的强干扰电平一般会超过邻近接收机的动态范围，造成接收机阻塞。由于跳频FH(Frequency Hopping)干扰信号的时变特性，使得跳频电台间同址干扰的处理变得更为复杂，因此，应用于跳频电台同址干扰抵消的自适应滤波算法应当满足收敛速度快、收敛精度高、处理非平稳信号鲁棒性能好等要求[10]。
自适应干扰抵消计算机仿真参数设计如下：有用接收信号和本地射频同址干扰信号均为MSK调制的跳频信号；干扰信号比有用信号强60 dB，本地耦合的参考信号比目标接收信号强50 dB、比射频干扰信号弱10 dB；仿真中干扰信号和目标接收信号频差200 kHz，各路信号的时延误差控制在4 ns以内[10]；滤波器阶数为4阶，在第400采样点时干扰信号的载频发生跳变，仿真结果如图4所示。
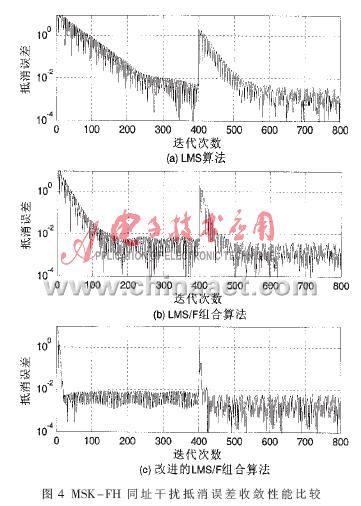
图4显示了LMS算法、LMS/F组合算法和改进的LMS/F组合算法在自适应跳频同址干扰抵消中的性能比较。改进的LMS/F组合算法大概经过30次迭代就可以进入稳态，相比于LMS/F组合算法的150次迭代和LMS算法的300多次迭代，其收敛速度上的优势非常明显；当第400个采样点载频跳变时，该算法也能更快重新收敛到稳态，表明其具有更好的鲁棒性能。由于LMF算法对附加噪声和信噪比非常敏感，因而在该仿真中，LMF算法不能收敛，其性能不能满足自适应跳频同址干扰抵消的要求，故在图4中未列出其性能曲线。
LMS算法应用于干扰抵消器时采用固定步长，存在收敛速度慢、失调量大的缺点。改进的LMS/F组合算法可以较好地解决收敛速度和稳态误差的内在矛盾、跟踪时变系统和降低干扰输出功率，为提高同址环境下跳频电台间的干扰抵消性能提供更好的途径。
本文引入修正因子γ对LMS/F组合算法进行改进，并进行了详细的理论分析，计算机仿真结果与理论分析相一致，表明了该算法的优良性能：改进的LMS/F组合算法参数调整简单高效、运算量小(与LMS/F组合算法相比基本不增加运算量)，在保证LMS/F组合算法的收敛精度和稳定性的基础上，进一步加快了算法的收敛速度。
参考文献
[1] MATHEWS V J. Adaptive polynomial filters[J]. IEEE Signal Processing Magazine, 1991,8(4):10-26.
[2] 高鹰, 谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报,2001,29(8):1094-1097.
[3] 覃景繁, 欧阳景正. 一种新的变步长LMS自适应滤波算法[J]. 数据采集与处理, 1997,12(2):171-174.
[4] 王敏强，郑宝玉. 一种新的可变步长LMS自适应滤波算法[J]. 信号处理,2004,20(6):613-617.
[5] WALACH E, WIDROW B. The least mean fourth (LMF) adaptive algorithm and its family[J]. IEEE Transactions on Information Theory, 1984,30(2):275～283.
[6] Pedro Inácio Hubscher, José Carlos M. Bermudez. An improved statistical analysis of the Least Mean Fourth (LMF)adaptive algorithm[J]. IEEE Transactions on Signal Processing, 2003,51(3):664～671.
[7] 李文元, 何雯, 刘梧林,等. 变权值LMF/LMS自适应多用户检测器[J]. 系统仿真学报, 2007,19(8):1793-1795.
[8] LIN S, HARRIS J G. Combined LMS/F algorithm[J].Electronics Letters, 1997,33(6):467～468.
[9] PARAITIS D L, CONSTANTINIDES A G. LMS+F algorithm[J].Electronics Letters,1995,31(7):1423～1424.
[10] KOWALSKI A M. Wideband co-site interference reduction apparatus[P]. Amecrican, 6693971, 2004.