摘 要: 介绍基于超声波测距技术的6自由度3-D输入设备的设计原理。采用检测渡越时间的方法,结合自动增益控制(AGC),自适应可变阈值技术和温度补偿技术,提高距离检测精度。经过空间解析几何运算,确定输入设备在空间坐标系中的位置和姿态。同时,检测按键的状态,确定所要实现的操作。可用于遥操作机器人系统中末端执行器的定位与定向、虚拟现实系统的3-D交互设备、头盔跟踪、视点导航和目标操纵等。
关键词: 3-D输入设备 定位与定向 超声波测距 遥操作机器人 虚拟现实
传统的2-D输入设备,如鼠标,轨迹球和绘图板等只能提供二维(平面)位置信息,不能提供其在空间坐标系中的三维位置和方向信息,从而限制了它们在未来3-D图形化人机交互界面系统,尤其是遥操作机器人和虚拟现实系统中的应用。
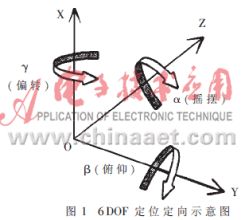
当前的3-D输入设备依据原理可分为机械式、电磁式、光学式、声学式和惯性式等[1]。由于声学式的3-D输入设备具有易于实现、成本低、对光线不敏感、无电磁辐射等优点,我们采用超声波测距技术来实现具有6个自由度(DOF)的3-D输入设备,并结合自动增益控制(AGC),自适应可变阈值技术和温度补偿技术,以提高距离检测精度,从而测得安装在输入设备上的超声波发射探头到三个接收探头的距离。经过空间解析几何运算,可得3-D输入设备在空间坐标系中的6个自由度信息:位置(x,y,z)和方向(γ,β,α)(即姿态,也就是绕X、Y和Z轴的旋转角),如图1所示。同时,检测3-D输入设备上的按键状态,确定所要实现的操作。
1 超声波测距
1.1 测距原理
输入设备的三维定位与定向基于一维测距技术。要实现三维定位与定向,就需要获得发射点到接收点的距离值。超声波测距的方法有多种:如相位检测法、声波幅值检测法和渡越时间检测法等[2]。相位检测法虽然精度高,但检测范围有限;声波幅值检测法易受反射波的影响。本文采用渡越时间检测法,其原理为:检测从发射换能器发出的超声波,经气体介质传播到接收换能器的时间,即渡越时间。渡越时间与气体介质中的声速相乘,便可得到超声波发射器和接收器之间的距离。
在3-D输入设备定位与定向系统中,选用工作频率为40kHz的PZT5压电陶瓷振动模式的超声波换能器。超声波测距原理结构框图如图2所示。三路超声波发射接收框图都相同,图2只画出了一路超声波发射接收框图。
1.2 渡越时间检测
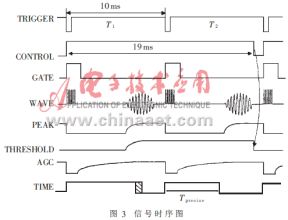
时序电路控制超声波换能器以固定的时间间隔来发射超声波。电路时序及各信号波形如图3所示[3]。
整个电路的时序由TRIGGER信号控制。CONTROL信号由TRIGGER信号负跳沿触发,它把触发周期T1和T2合并为一个检测周期,这样是为了达到可变阈值检测的目的。其中,T1为精密峰值检测周期,T2为可变阈值检测周期。GATE信号是为了屏蔽虚假接收波。WAVE信号为超声波发射及接收信号。发射的脉冲数应选择合适,脉冲个数多有不少优点:脉冲能量大,受其它声波模式影响较小等;但脉冲个数多,盲区大,且余振波头也多。通过实验,取4个脉冲。PEAK信号是精密峰值信号,由积分充电电路得到。由于接收波随距离增加迅速衰减,为了使接收波的幅值不随测量距离的变化而大幅度地变化,采用可变增益控制(AGC)技术,有利于获得精确的距离信息。
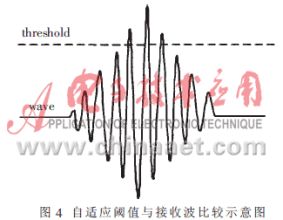
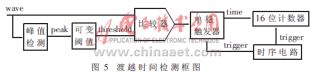
THRESHOLD信号为自适应可变阈值信号,它反映前一周期接收波信号的幅值大小。相邻两个接收波信号的峰值相差不大,将T1周期得到的精密峰值乘以一个比例因子,得到THRESHOLD信号,作为T2周期的阈值,和WAVE信号相比较,保证每次在同一个接收波头(在本系统中,n=4)后开始封锁计数器,获得渡越时间(如图4和图5),从而不受接收波幅值大小的影响,提高了测量的精度。
1.3 距离计算和温度补偿
超声波发射点到接收点的距离D为:

因此,温度每变化1度,声波的速度变化0.6(mm/ms)。若渡越时间达到9ms(距离约为3m),就会产生约5mm的误差。温度变化2度时,则产生约1cm的误差,因而必须进行温度补偿。
用4MHz的方波信号作为计数脉冲,计数器的时间分辨率为Tres=0.25×10-3(ms)。设在渡越时间ttof内,计数器的值为ncount,由于计数器是在第n个接收波头后被封锁,则有:

这种采用检测超声波渡越时间的方法,结合自动增益控制(AGC)和自适应可变阈值技术,并加入温度补偿,提高了距离检测精度,有利于获得3-D输入设备精确的位置和姿态信息。
2 6DOF输入设备的设计原理
2.1 三维定位原理
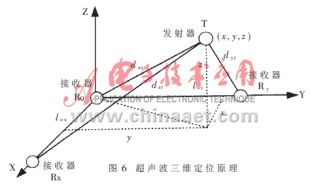
根据三角测量原理可以实现三维定位。在参考坐标系的原点、X轴和Y轴分别安装上三个超声波接收器Ro、Rx、Ry,在输入设备上安装超声波发射器T,其在参考坐标系中的位置为(x,y,z),如图6所示。
设Ro与Rx之间的距离为lox,Ro与Ry之间的距离为loy。通过超声波测距,测出Ro到发射器T的距离为dot,Rx到发射器T的距离为dxt,Ry到发射器T的距离为dyt,根据三角测量原理,有(6)式,可解得发射点T的三维直角坐标表示形式,如式(7)所示。

2.2 三维定向原理
要进行三维定向测量,需在输入设备上安装三个超声波发射器Ta、Tb、Tc,这三个发射点在参考坐标系中的位置可通过上述的方法依次获得,如图7所示。
三角形TaTbTc所在坐标系为Tx-y-z,它在参考坐标系Bx-y-z中的位置与姿态的描述可用一个4×4的变换矩阵 表示[4]:
表示[4]:

设三角形TaTbTc三条边的中线交点为T。定义坐标系Tx-y-z:T为坐标原点,三角形的法线D为坐标系Tx-y-z的z轴、TTa为坐标系Tx-y-z的x轴,y轴则由右手法则确定。则变换矩阵 描述了坐标系{Tx-y-z}相对于参考坐标系{Bx-y-z}的方位,即有:
描述了坐标系{Tx-y-z}相对于参考坐标系{Bx-y-z}的方位,即有: :Tx-y-z→Bx-y-z。于是,法线D的方向矢量为:
:Tx-y-z→Bx-y-z。于是,法线D的方向矢量为:

三角形TaTbTc三条边的中线交点T在参考坐标系BX-Y-Z中的位置(xT,yT,zT)可由下式求出:

经归一化后,变换矩阵为:
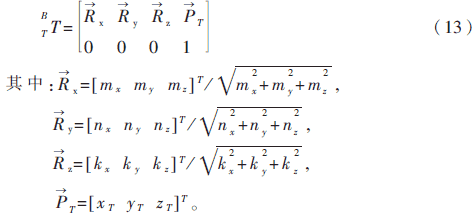
然后,根据(8)式就可求出3-D输入设备在参考坐标系Bx-y-z中的6个自由度信息:位置(x,y,z)和方向(γ,β,α)(即姿态,也就是绕X、Y和Z轴的旋转角)。从中可知,只要测出三个超声波发射器到三个超声波接收器的距离,经过空间解析几何运算,就可求出描述输入设备位置与姿态的变换矩阵。
3 实验
基于超声波测距技术的3-D输入设备系统主要是由三路超声波检测电路、温度补偿电路和89C51单片机数据采集系统组成。单片机通过RS232串行口把3路ncount、温度Tenv以及按键K1和K2的闭合情况传送给上位机。数据通信的波特率为19.2Kbps。数据发送格式为:
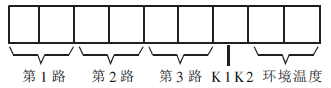
三路计数值和环境温度用两个字节表示,低位在前,高位在后;K1和K2用一个字节的低两位表示,1表示断开,0表示闭合,且bit0代表左键K1的闭合情况,bit1代表右键K2的闭合情况。上位机接收到各测量值后,根据空间解析几何法计算出输入设备在参考坐标系中的位置和姿态,完成6DOF输入设备的三维定位与定向。并根据按键K1和K2的闭合情况,确定所要实现的操作。
3-D输入设备的设计关键在于精确的距离测量。为了检验本系统测距的精确度和可靠性,我们在实验室中把超声波发射装置安装在机器人MOVEMASTER-EX的末端执行器上,这样机器人的末端执行器就相当于一个3-D输入设备,在工作平台上安装三个超声波接收器。实验时,移动机器人到任一位置,通过本系统测量超声波发射装置在空间参考坐标系中的三维位置(x,y,z)和方向(γ,β,α)(即姿态,也就是绕X、Y和Z轴的旋转角),并和末端执行器的真实位置与姿态做比较,测量值和真实值是一致的。其中,距离测量误差在满量程3m的范围内可达±0.2mm,三维位置坐标在1m3工作空间内的最大误差为±3mm。由于缺乏精确的旋转角度测试平台标准,没有进行有关(接上页)
旋转角度的误差试验。实验表明了这种基于超声波测距技术的6DOF输入设备的定位与定向方法的有效性和可靠性。
本文提出了基于超声波测距技术的3-D输入设备的设计原理和方法。除了可提供输入设备在三维(空间)坐标系中的位置和姿态的6个自由度信息外,还克服了传统机械式、光电式等二维(平面)输入设备,如鼠标、轨迹球易磨损,易受粉尘影响等缺点。可用于机器人操作手的空间定位与定向,3-D图形化人机交互系统的输入设备,以及虚拟现实系统中的头盔跟踪、视点导航和目标操纵等领域。具有精度高、成本低、易于实现、抗电磁干扰能力强,对光线不敏感、无电磁辐射等优点。
参考文献
1 Chris Hand.A Survey of 3-D Input Device. Technical Report TR94/2, Department of Computer Science, De Montfort University, UK, 1994
2 Hans W.When, Pierre R. Belanger.Ultrasound-Based Robot Position Estimation.IEEE Transactions On Robotics and Automation, 1997;13(5):682~692
3 Peng Gang, Xiong Chunshan, Huang Xinhan.Design of 3-D Mouse Using Ultrasonic DisTance Measurement.Proceedings of SPIE: International Conference on Sensors and Control Techniques (ICSC 2000),2000;(6)226~229, Wuhan, China
4 Ruhard P.Paul. Robot Manipulators:Mathematics, Programming and Control.Massachusetts:The MIT Press,1981