摘 要： 针对K-means算法中的初始聚类中心是随机选择这一缺点进行改进，利用提出的新算法选出初始聚类中心，并进行聚类。这种算法比随机选择初始聚类中心的算法性能有所提高，具有更高的准确性。
关键词： 欧氏距离；K-means；优化初始中心
数据挖掘技术研究不断深入与发展，作为数据挖掘技术中的聚类分析，也越来越被人们关注与研究。聚类分析是数据挖掘中一个非常活跃的研究领域，并且具有广泛的应用。聚类就是将数据集划分成若干簇或者类的一个过程[1]。经过聚类之后，使得同一簇中的数据对象相似度最大，而不同簇之间的相似度最小。
聚类是一种无监督的学习算法，即把数据对象聚成不同的类簇，从而使不同类之间的数据相似度低，而同一个类中的相似度高，并且将要划分的类是之前不知道的，其形成由数据驱动。聚类算法[1]分成基于划分的、密度的、分层的、网格的、模型的。其中基于划分的聚类算法中的K-均值算法(K-means算法)是最常用的一种聚类算法，同时也是应用最广泛的一种算法。K-means聚类算法主要针对处理大数据集时[2]，处理快速简单，并且算法具有高效性和可伸缩性。但是K-means算法也有一定的局限性[3]，如K值必须事先给定，只能处理数值型数据，初始聚类的中心是随机选择的，而其聚类结果的好坏直接取决于初始聚类中心的选择。并且由于初始聚类中心随机选择，容易造成算法陷入局部最优解。因此初始聚类中心的选择十分重要。
本文针对随机选择初始聚类中心的缺点，提出了一种新的改进的K-means聚类算法。该算法产生的初始聚类中心不是随机的，能够很好地体现数据的分布情况，使得初始中心尽可能地趋向于比较密集的范围内，从而进行更好的聚类，最终消除了传统K-means算法中由于初始聚类中心选择是随机的而产生的缺点。最后实验证明了这种算法的有效性与可行性。
1 传统K-means算法
1.1 传统K-means算法的思想
传统的K-means算法的工作流程[1，4]：首先从n个数据对象任意选择k个对象作为初始聚类中心；而对于所剩下其他对象，则根据它们与这些聚类中心的相似度(距离)，分别将它们分配给与其最相似的(聚类中心所代表的)聚类；然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值)。不断重复这一过程直到标准测度函数开始收敛为止。一般都采用均方差作为标准测度函数。其准则函数定义如下：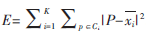
。其中，E为数据集中的对象与该对象所在簇中心的平方误差的综合，E越大说明对象与聚类中心的距离越大，簇内的相似性越低，反之则说明相似性越高；p是簇内的一个对象，Ci表示第i个簇，xi是簇Ci的中心，k是簇的个数。
传统的K-means算法具体描述如下[5]：
输入：k，data[n]；
输出：K个簇的集合。
(1)任意选择k个对象作为初始中心点，例如c[0]=data[0]，…c[k-1]=data[k-1]。
(2)根据簇中对象的均值，将每个对象指派给最相似的簇。
(3)更新簇均值，即计算每个簇中对象的均值。
(4)重复步骤(2)、(3)，直到不再发生变化。
1.2 传统K-means算法的局限性
传统的K-means算法中对于K个中心点的选取是随机的 [ 3]，而初始点选取的不同会导致不同的聚类结果。为了减少这种随机选取初始聚类中心而导致的聚类结果的不稳定性，本文提出了一种关于初始聚类中心选取的方法，用来改变这种不稳定性。
即所有样本点的两两之间的距离之和除以样本点n的组合数。
2.2 改进算法流程
本算法的改进建立在没有离群点的数据集上，针对没有离群点的数据进行分析。
输入：样本点，初值k。
输出：k个簇的聚类结果，使平方误差准则最小。
步骤：
(1)求出两两样本点之间的距离存入矩阵D中。
(2)初始化集合A以及中心点集合Center，最小距离的样本点放入集合A中，并求出其中心最为第一个初始的聚类中心z1。
(3)求出次小距离的样本点的中心，然后求出此中心与z1之间的距离，与Meandist进行判断。如果小于Meandist，则将此样本点加入A中，再求第三距离小的样本点，重复步骤(3)；如果大于Meandist，则求出此中心存入Center。
(4)Until集合Center中的个数等于k，初始聚类中心全部找到。
(5)用找到的初始聚类中心进行K-means聚类。
算法举例：
如图1所示，假设有20个点数据集，并且已经将孤立点排除，需要将其聚成k=3类。首先计算两两之间的距离，利用定义2求出Meandist，并找出最小的距离(如图中的x1、x2)；然后求出其中心，用红色表示；找出距离次小的距离(如图中的x3、x4)，计算出x3、x4的中心，并加一步判断。如果这个中心与前面求出的一个聚类中心之间的距离小于Meandist，那么就排除这个聚类中心，接着执行找第三小的距离，并求其中心，直到找到K个初始聚类中心为止；反之，则求下一个初始聚类中心，直到找到k个初始聚类中心为止。
3 实验分析
为了便于分析与计算，本文采用的是二维数据，并且数据类型是实型的，实验环境为MATLAB。为了进行对比，分别采用了传统的K-means算法与本文改进的K-means算法进行比较。
本文实验采用了两组实验进行验证，一组是随机数据，一组是标准数据库集。
(1)采用随机数据
本文用随机产生的80个样本分别采用传统的K-means算法进行聚类与本文的改进算法进行聚类，比较其聚类结果图。
传统算法采用随机选取初始聚类中心有(0.950 1， 0.794 8)、(0.231 1，0.956 8)、(0.606 8，0.522 6)，其聚类结果如图2所示。
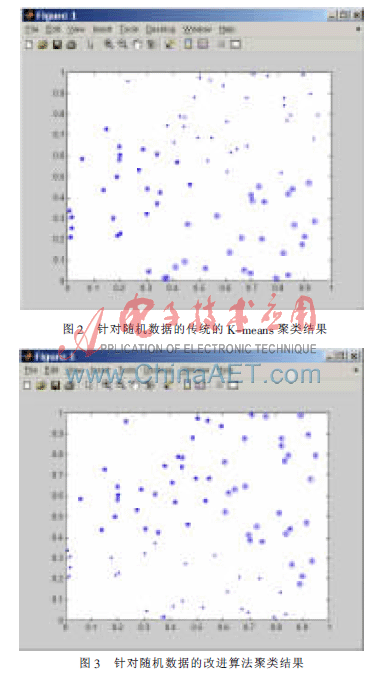
采用改进算法的初始聚类中心有(0.339 9、0.028 4)，(0.200 7，0.591 4)、(0.724 8，0.381 9)，其聚类结果如图3所示。
(2)采用标准数据集：Iris数据集
本文采用了Iris数据集，它是UCI数据库中的一个标准数据集。Iris数据集包含有4个属性，150个数据对象，可分为三类。选用Iris数据集前二维的数据进行聚类。分别用传统算法和改进算法进行聚类，其中分别用实心点、圈实心点以及五角星表示这三类。
传统算法采用随机选取初始聚类中心有(0.950 1， 0.582 8)，(0.231 1，0.423 5)、(0.606 8，0.515 5)，其聚类结果如图4所示。
采用改进算法的初始聚类中心有(0.009 9，0.015 0)、(0.294 2，0.639 2)、(0.651 2，0.190 5)，其聚类结果如图5所示。
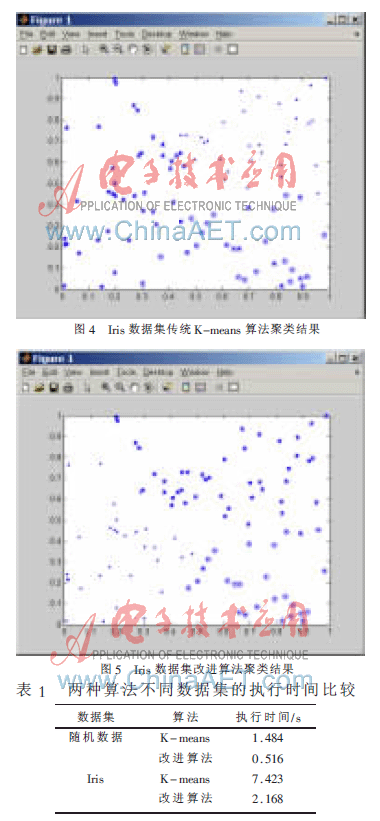
对比这两幅图的聚类结果可以看出，采用改进算法产生聚类结果比较稳定准确。
运用K-means算法和本文改进算法针对随机数据和Iris数据分别实验得出的时间如表1所示。
K-means算法是应用最为广泛的一种基于划分的算法，但是由于其初始中心的选择是随机的，从而影响了聚类结果，使得聚类结果不稳定。本文主要是针对传统K-means算法的这一缺点，提出了一种新的改进算法，即基于平均距离的思想，进行初始聚类中心的选择。实验证明，该算法是切实可行的，与传统的K-means算法比较，有较好的聚类结果以及较短的运行时间。但本文算法是基于先将噪声点排除掉之后应用此改进算法进行聚类、且是在点的分布比较均匀的前提下应用，才有良好的效果。如果对于具有噪声点的数据集有一定的局限性、而且是比较密集的点的情况下，这将在以后的学习研究中进行探讨。
参考文献
[1] HAN J， KAMBER M. 数据挖掘概念与技术[M].范明，盂小峰，等译.北京：机械工业出版社，2006.
[2] 孟海东，张玉英，宋飞燕.一种基于加权欧氏距离聚类方法的研究[J].计算机应用，2006，26(22)：152-153.
[3] 包颖.基于划分的聚类算法研究与应用[D].大连：大连理工大学，2008：18-20.
[4] 李业丽，秦臻.一种改进的K-means算法[J].北京印刷学院学报，2007，15(2)：63-65.
[5] 张玉芳，毛嘉莉，熊忠阳.一种改进的K-means算法[J].计算机应用，2003，23(8)：31-33.
[6] 袁方，周志勇，宋鑫.初始聚类中心优化的k-means算法[J].计算机工程，2007，33(3)：65-66.