摘 要: 基于NI公司的PXI-1050工控机和PXI-7344运动控制卡,在LabVIEW环境下开发了直线二级倒立摆LQR控制系统的仿真与实时控制实验平台。该平台提供了LQR控制器的设计与仿真验证工具,以及实时监控环境,同时利用LabVIEW软件中的3D控件设计了可视化的人机交互界面。该平台可以为控制理论研究与教学提供良好的硬件在环实验环境,操作方便并且具有一定的开放性。
关键词: 倒立摆;最优控制;运动控制卡;硬件在环;人机交互
LabVIEW是由美国国家仪器公司(NI)开发的一种图形化编程语言,它广泛地被工业界、学术界和研究实验室所接受,视为一个标准的数据采集和仪器控制软件,具有可视化、编程方便等特点[1]。NI公司的PXI-1050工控机带有8个PXI插槽,配合图像处理、数据采集、运动控制、嵌入式系统等模块,可以构成快速原型开发系统。在PXI-1050工控机上,利用LabVIEW软件可以开发硬件在环仿真实验平台。与MATLAB软件工具相比较,LabVIEW在硬件接口驱动、人机交互界面的设计方面更为方便。
倒立摆是一种典型的非线性不稳定系统,在控制理论算法验证和课程教学中,将倒立摆作为经典被控对象开发的实验装置有广泛的应用价值。本文以LQR控制算法为例,介绍了直线二级倒立摆控制系统的设计与实现。该系统提供了一个控制器设计、仿真和实时控制实验平台。根据二次型最优指标,用户可以进行控制器参数设计、仿真调试和倒立摆的实时控制验证,并且通过倒立摆3D模型和响应曲线图直观地显示实际倒立摆运动情况。
1 二级直线倒立摆的数学模型
二级倒立摆物理系统是由小车和安装在小车上的一级摆杆和二级摆杆组成。其中实际模型的参数如表1所示。



2 倒立摆系统的硬件设计
本文设计的倒立摆控制系统采用NI公司的PXI-1050工控机为核心,控制系统的硬件结构如图1所示。
摆杆角度和小车位置的测量采用3个OVW2-06-2MD编码器。
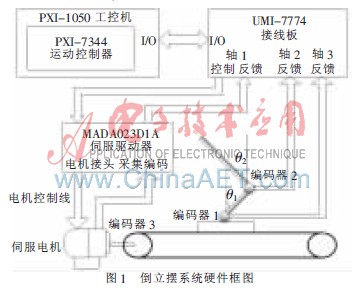
PXI-7344的运动控制卡是NI公司的一款中档的4轴步进/伺服控制器,每轴可通过软件设置步进/伺服控制器的类型和参数,结合LabVIEW Motion驱动软件,可实现各种类型的控制任务。运动控制卡内部高性能微处理器(DSP)完成控制器计算后,向交流伺服电机的驱动器发出控制指令[3]。
UMI-7774接线板为运动控制卡提供了丰富的布线和连接点,从而简化了PXI-7344控制器与第三方驱动器、放大器、编码器和限位开关之间的集成,同时也起到了过电流保护和信号隔离的作用[4]。
交流伺服电机驱动器采用日本松下公司的 MSDA023D1A,它的作用是接收外部控制信号控制PWM输出,调节电机转速。同时可在其内部形成速度控制环。
在图1所示倒立摆系统中,交流伺服驱动器一方面采集编码器3的信号,在其内部形成速度控制环,同时将编码器3的信号送入UMI-7774接线板。PXI-7344运动控制卡通过接线板采集编码器1~3的脉冲信号,以及倒立摆底座上两个限位开关的数字信号。通过PXI-1050工控机的LabVIEW软件系统,将编码器1和编码器2的脉冲计数转化为摆杆1和摆杆2的角度读数,将编码器3的脉冲计数转化为小车的水平位置,并按照一定的控制策略计算出小车的给定加速度,经运动控制卡内部控制器计算得到的控制量送入伺服电机驱动器,控制电机的加速度,实现对直线二级倒立摆的控制。限位开关输出的数字信号用来决定相应的关闭操作[5]。

3.2 LQR控制器在LabVIEW中的实现
LabVIEW中的控制与仿真工具箱提供了LQR函数,该函数允许输入两个参数Q和R,这两个参数用来分配性能指标中控制量和状态偏差量的权重。LQR函数的输出参数是使二次型性能指标最优的状态反馈矩阵K。
在倒立摆LQR控制中,设R为某一固定值,Q=diag(Q11,Q22,Q33,0,0,0),其中Q11代表小车位移的权重,Q22代表摆杆1角度偏差的权重,Q33代表摆杆2角度偏差的权重。权重值增大,对相应的偏差量抑制能力增强。
本文通过二级倒立摆模型与LQR函数结合设计了倒立摆仿真VI。图3是VI的前面板。用户可通过前面板的左侧修改模型参数、R值以及Q阵的权值,在前面板的右侧可得出仿真的曲线图,同时在图4的程序框图中,还可设置系统的仿真步长和仿真时间,默认的仿真步长为0.01。
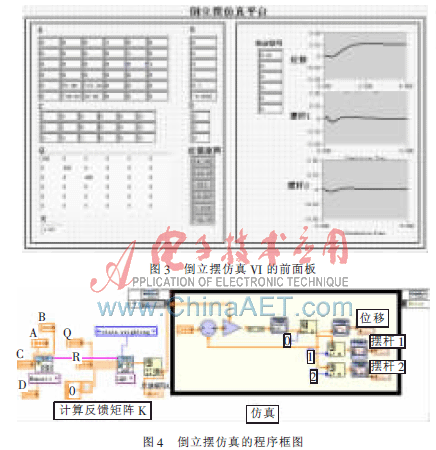
当取参数Q11=200,Q22=400,Q33=400,仿真步长为0.01,仿真时间为10 s时,在LabVIEW仿真平台上可以得到小车位置、摆杆1以及摆杆2的仿真曲线图。由图3可以看出三者的超调量很小、上升时间也很短,具有一定的抗扰能力。
4 二级倒立摆的实时控制
4.1 角度测试VI程序
在倒立摆实时控制系统设计中,为了测试所编写的程序能否正常采集摆杆1和摆杆2的角度数据,本文编写了摆杆角度测试程序。
通过运动控制卡PXI-7344采集的摆杆角度数据可以在程序的前面板上显示出来。程序开始执行时,摆杆处于垂直向下静止状态,编码器输出的脉冲数和换算后的弧度值均为0。当人为地提起摆杆时,上述两个数值立即随着摆杆角度变化,可以方便地用来对编码器进行角度标定。
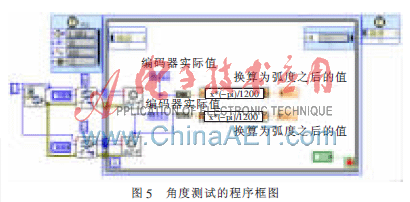
图5是角度测试的框图程序。倒立摆控制对实时性要求高,本文设置的定时循环的采样时间是10 ms。程序包括控制器初始化,控制器各个轴的设置和复位以及定时循环采样。在每次循环中,调用了采集角度编码器的驱动函数,对各个摆杆采集一次数据。在显示控件中将编码器的实际脉冲数读出来,换算成弧度值。
4.2 倒立摆实时控制系统的设计
在倒立摆实时控制系统设计中,本文利用LabVIEW良好的人机交互功能,设计用户操作界面。使用LabVIEW8.6版本所提供的3D控件功能,搭建了一个直线二级倒立摆3D模型。在实时控制过程中,根据采集的小车位置和两个摆杆角度的数据,将倒立摆实际运动情况反映到虚拟的3D模型中。
在二级直线倒立摆LQR控制实验平台的用户操作界面上,选择“实时控制”选项卡时,并选择“参数设置及显示界面”如图6所示,设置反馈矩阵K的值,这六个值来自于仿真的结果。点击“开始控制”按钮,小车位置、摆杆1弧度值、摆杆2弧度值以及左右限位开关状态等数字信号反映到前面板上来,从而达到监控的目的。
选择“数据显示界面”选项卡,如图7所示,可显示直线二级倒立摆3D模型和小车位置、摆杆1角度、摆杆2角度的曲线图,并观察各个摆杆的振荡情况,而且可以通过在3D图形中旋转操作,选择从不同的角度观察3D演示。
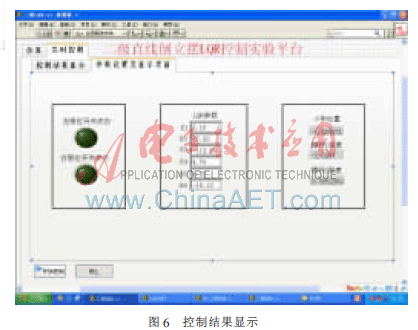
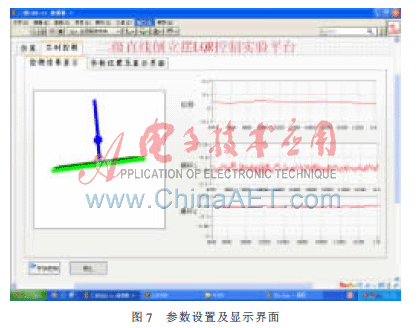
点击图6下方的“停止”按钮,整个倒立摆控制程序停止运行。
本文基于NI公司的PXI-1050工控机和PXI-7344运动控制卡,在LabVIEW环境下开发了直线二级倒立摆LQR控制系统的仿真与实时控制实验平台。该实验平台提供的仿真工具可以根据给定的二次型指标,方便地完成最优状态反馈矩阵K的设计和仿真验证。利用系统提供的实时控制工具,可以进行参数设置和监控。用户界面提供的倒立摆3D运动模型、输出响应曲线和实时数据可以全面显示倒立摆的实时控制效果。该平台具有开放性和扩展性。
参考文献
[1] 杨忠仁.基于LABVIEW数据采集系统[J].重庆大学学报(自然科学版),2007,24(2):32-35.
[2] 刘文斌,干树川.二级倒立摆的建模与MATLAB仿真[J].自动化与仪器仪表,2008(5):6-7.
[3] Motion Control National Instruments 7344 User Manual. http://sine.ni.com/psp/app/doc/p/id/psp-493/lang/zhs/
[4] Motion Control National Instruments Universal Motion Interface(UMI)-7774/7772 User Manual. http://sine.ni.com/nips/cds/view/p/lang/zhs/nid/12534.
[5] 李艳萍.基于LabVIEW的运动控制系统的设计[J].中国科技信息,2009(22):95-96.
[6] Chaiporn Wongsathan,Chanapoom Sirima. Application of GA to Design LQR Controller for an Inverted Pendulum System[C]. International Conference on Robotics and Biomimetics, 2009, 951-954.
[7] Jyoti Krishen,Victor M. Becerra. Efficient Fuzzy Control of a Rotaty Inverted pendulum Based on LQR Mapping[C]. International Symposium on Intelligent Control, 2006,2701-2706.
[8] Hongliang Wang. Design and Simulation of LQR Controller with the Linear Inverted Pendulum[C]. 2010 International Conference on Electrical and Control Engineering 699-702.

