求解多目标投资组合优化模型的遗传算法
2009-06-17
作者:王怀柱
摘 要:针对考虑最小交易量、交易费用,以及单项目最大投资上限约束的多目标投资组合模型,对目标函数添加惩罚函数项来处理约束条件的方法。本文通过对交叉算子、变异算子的改进,设计了一种遗传算法进行求解。实验算例表明,该算法是有效的。
关键词:投资组合;多目标;遗传算法;异常变异
风险投资具有高风险、高收益、高增长潜力和高技术的特点,如何增加风险投资的收益潜力,降低风险,是极其重要的。
在金融市场众多可供投资的风险或无风险资产中(股票、债券、投资基金、权益产品、银行存款等), 选择适当数量的资产, 进行合理的组合投资, 可以减小投资的风险, 确保投资的收益。Markowitz[1]于1952年提出的均值-方差组合模型是在禁止融资和没有无风险借贷的假设下,以个别股票收益率的均值和方差找出投资组合的有效前沿(Efficient Frontier),即一定收益率水平下方差最小的投资组合。这是一个二次规划问题,利用传统的优化方法容易求解。
最小交易量和交易费用是投资组合中的重要因素,最小交易量是单笔交易中最小的交易数量,我国上海和深圳交易所的股票交易中,最小交易量为100股,近来投资组合优化问题的研究中有些考虑了最小交易量[2-3]。 交易费用是指交易中所要支付的费用。没有交易费的证券组合投资将导致证券市场的无序。我国为了规范证券市场,在交易中要征收个人所得税、印花税等费用。参考文献[4]、[5]也有考虑。参考文献[6]中同时考虑了最小交易量和交易费用,建立了一个改进的多目标投资组合优化模型。该模型是一个带有很强约束的混合整数二次规划模型。针对这一模型,本文通过对目标函数加入惩罚项的方法,使得约束条件降弱,对转化后的模型,运用一种改进的整数编码的遗传算法进行求解,数值实验表明,该算法是有效的。
1 考虑最小交易量和交易费用的投资组合模型
1.1 传统的多目标投资组合优化模型
设有N种不同的投资项目,xi,i=1,2…,N表示投资各个项目所占总投资金额的比重,μi表示投资项目i的期望收益率,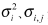 分别表示投资项目i收益率的方差及与投资项目j收益率的协方差的无偏估计:
分别表示投资项目i收益率的方差及与投资项目j收益率的协方差的无偏估计:
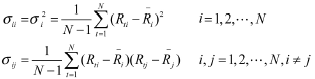
则投资组合的期望收益可表示为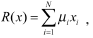
投资组合的风险表示为:
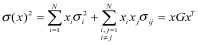
对投资者来说,总是希望投资的期望收益尽可能的大,同时风险又尽可能的小,因此就得到了目标函数,即:
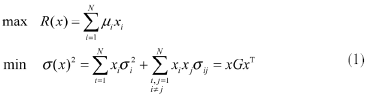
令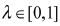 表示投资者对风险的厌恶指数,则(1)式可转化为:
表示投资者对风险的厌恶指数,则(1)式可转化为:
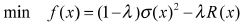
当λ=0表示投资者更关注收益,是收益最大化,并没有考虑风险;当λ=1,表示投资者更关注风险,而不考虑收益。再加上对投资总额的限制,可以得到传统的多目标投资组合优化模型:
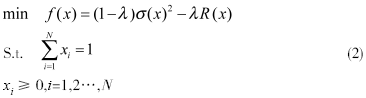
1.2 改进的多目标投资组合优化模型[6]
假设投资总金额为C,可允许的最小值和最大值为C0和C1,假设最小交易量为NB个基本单位,投资i的单位价格为Pi,则投资i的最小投资金额为ci=NB×pi。设一种投资组合k=(k1,k2,…,kN),则投资的总金额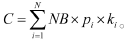 。设交易费用为g(C),则投资组合的期望收益率为:
。设交易费用为g(C),则投资组合的期望收益率为:
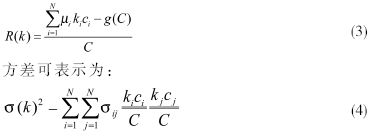
设μi为投资i允许的最大投资金额,则可得到改进的多目标投资组合优化模型:
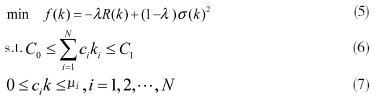
这是一个混合整数的二次规划问题,是NP完全问题,用传统的优化方法很难求解。根据优化方法,在目标函数中加入惩罚项来处理约束,如式(6),设M是一个大自然数,则模型转化为: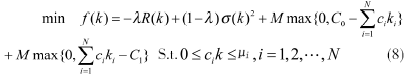
当投资组合不满足式(6)时,式(8)的目标函数值将会很大,而投资组合就受到惩罚,从而达到与约束式(6)相同的约束作用。
2 整数编码的遗传算法
2.1遗传算法的改进策略
2.1.1编码策略
传统的遗传算法是二进制编码,采用整数编码的策略,每个染色体对应一种投资组合,直接用整数向量k=(k1,k2,…kN)表示,每个ki的取值在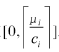 之间,其中
之间,其中 为下取整运算。这样得到的编码可满足式(7)。
为下取整运算。这样得到的编码可满足式(7)。
2.1.2 交叉策略
本算法采用单个染色体,单点交叉的策略,即任意两个染色体的任意位的等位基因相互交叉。
2.1.3 变异策略
本算法采用群体变异策略,即所有染色体,每个基因位都等概率地发生变异,变异算子如下:

其中β为变异步长,取正整数。
2.1.4 异常变异策略
为了防止算法早熟,采用了异常变异策略,当交叉和变异进行了D代之后,或者种群的适应度聚度超过某一阈值α之后,整个群体发生无方向变异(最简单的方法是重新初始化种群),受参考文献[7]的启发,适应度聚度如下:
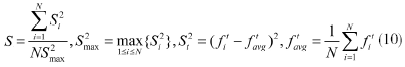
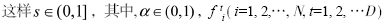 表示交叉和变异t代时染色体i的适应度(文中取为适应值)。
表示交叉和变异t代时染色体i的适应度(文中取为适应值)。
2.2遗传算法步骤
(1)参数设定:设定种群规模为N,进化代数为H,异常变异发生代数为D,异常变异的适应度聚度阈值为α。
(2)初始化种群:根据编码策略初始化种群,记录最优值。
(3)交叉和变异:按照法则进行交叉和变异,更新最优值。
(4)异常变异:若交叉和变异代数等于D,或者适应度聚度满足S≥α,则转到(2)。
(5)终止检验:若满足进化终止准则,终止计算,输出最优值。
3 仿真算例
考虑如下的投资组合问题:有6种股票,表1给出了6种股票8个时间段的收益率,表2给出了6种股票的协方差,表3给出了6种股票的价格。
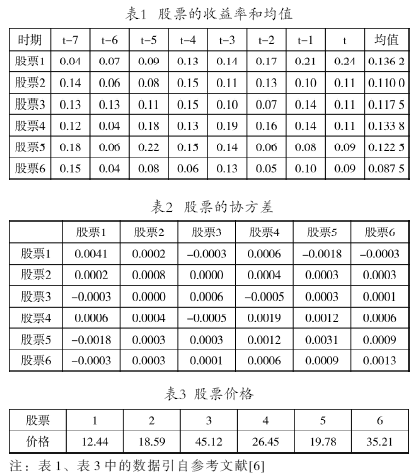
假设股票的最小交易量NB=100,C0=1 000 000,C1=1 005 000,并令每种股票的最大交易金额μi=200 000,i=1,2…,N,交易费用设为0.01C,分别取λ=0、0.2、0.4、0.6、0.8、1.0,阈值取α=0.8、0.85、0.9,种群规模为50,进化代数为2 000,异常变异代数为50,变异步长为1,在Genuine Intel(R) CPU T2050 @1.60 GHz、1.05 GHz、1.00 GB内存的计算机上用Matlab7.0编写程序进行计算,每次计算独立运行50次,取其平均值,结果如表4所示。
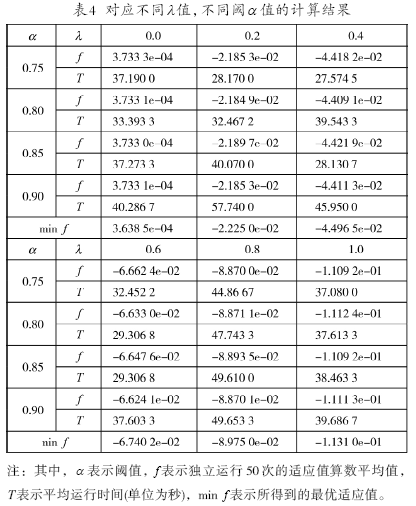
由表4可以看出:
(1)该算法求解上述模型得到了很好的结果,计算时间不超过1min;
(2)对于取不同阈值得到的平均适应值与最优适应值的相对误差在10-2之内,说明算法是稳定的。
(3)当阈值取0.85左右时,效果更好。
(4)平均计算时间随阈值的增加而增加。
本文针对考虑最小交易量、交易费用以及投资项目的最大上限约束的多目标投资组合优化模型,通过在目标函数中加入惩罚项来处理投资总金额的约束,将模型的约束条件弱化,并提出了一种整数编码的遗传算法,该算法求解多目标投资组合优化模型是可行的、有效的。
参考文献
[1] Markowitz H. Portfolio selection[J]. Journal of Finance,1952,7(1):77-91.
[2] Kellerer H, Mansini R, Speranza M G. On selecting a portfolio with fixed costs ang minimum lots[J].Annals of Oprations Research,2000,99(3):287-304.
[3] Fernandez A, Gomez S. Portfolio selection using neural networks. Computer & Operations Research.2007;(34):1177-1191.
[4] Chang T J, Meade N, Beasley J, et al. Heuristics for cardinality constrained portfolio optimization.Computer & Operations Research, 2000(27):1271-1302.
[5] 赵娟,李科学. 有交易费的证券组合投资优化模型. 华北水利水电学院学报, 2006, 27(2):110-112.
[6] 林丹,李小明,王萍. 用遗传算法求解改进的投资组合模型. 系统工程,2005, 23(8): 68-72.
[7] Duan Yu Hong,GAO Yue Lin, LI Ji Min. A new adaptive particle swarm optimization algorithm with dynamically changing inertia weight. Intelligent Information Management Systems and Technologies, 2006, 2(2): 245-255.

