摘 要：曝气机搅拌轴在工作过程中，主轴断裂时有发生，其可靠性优化设计问题十分重要。本文通过对人工神经网络的学习研究，以搅拌轴重量为目标函数、以轴的强度和刚度为约束条件，构造了曝气机搅拌轴优化设计数学模型，优化效果显著。
    关键词：人工神经网络；搅拌轴；优化设计

    倒伞曝气机在环境保护和农业生产中得到了广泛应用。随着科学技术和生产发展的需要，具有性能好、动力效率高、能耗低特点的大功率、大直径倒伞曝气机开始出现。但是在实际应用中，主轴断裂问题时有发生。虽然加大主轴的直径可以改善这一问题，但会增大成本和功率消耗。本文采用人工神经网络自学习优化特点，以搅拌轴重量为目标函数、以轴的刚度和强度为约束条件，去构造大功率曝气机搅拌轴优化设计数学模型，并通过设计实例验证其模型的可行性和优化效果。
1 BP神经网络模型
    目前，在人工神经网络的实际应用中，绝大部分采用BP网络和它的变化形式。Kolmogorov定理定义：对于任一映射φE^m→R^m,φ(X)=Y(E为单位闭区间)，φ可以精确地由三层神经网络实现，且该神经网络的第一层有m个神经元，中间层有(2m+1)个神经元，第三层有n个神经元。从理论上已证明了任意一个映射都能通过一个前向三层神经网络来实现，从而在数学上保证了三层BP神经网络的高度非线性映射能力。一个三层BP神经网络映射关系如下所示^[1]。
    具有r个输入和一个隐含层的BP神经网络模型结构，其输入为：
    p=[p¹, p²,…，p^q]=[p¹，p²，…p_r]^T，
    pⁱ=[p_1i, p_{2 i},…p_ri]^T，i=(1,2…)q,
    p_j=[p_j1, p_j2 ,…p_jq]^T，j=(1,2…r)，
    通过权值矩阵w1，阈值矩阵B1与神经元s1相连，每个神经元通过一个求和符号，在与输入矢量p_j(j=1,2…r)进行加权求和运算后，形成神经元作用函数f1的输入，并经神经元作用函数f1，得到输出A1，A1又作为神经元s2的输入，通过权值矩阵w2、阈值矩阵B2与神经元s2相连，再经求和、加权运算后作为神经元作用函数f2的输入，经神经元作用函数f2，得到输出A2,用公式表示为：
   
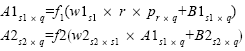
    在BP神经网络中，神经元作用函数f(x)一般为(0,1)S型函数：

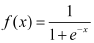
    该函数是一个连续可微的函数，因此，可以严格利用梯度法进行推算，其权值修正的解析式十分明确。
2 曝气机主轴BP神经网络模型
2.1 建立神经网络模型
    应用神经网络方法进行多失效模式相关的可靠性优化设计，其主要过程如下：
    ⑴ 根据给定的零部件系统可靠度设计要求，应用简单界限估计法，初步确定各失效模式可靠度的界限。
    ⑵ 先不考虑各失效模式之间的相关性，仅以各失效模式的可靠度作为约束条件进行优化设计，得到初始设计点。
    ⑶ 在初始设计点附近的有限邻域内，对设计变量进行不同水平的组合，应用随机模拟方法进行可靠性分析。
    ⑷ 建立神经网络模型，将可靠性分析获得的设计变量和可靠度数据作为神经网络的训练样本。通过网络训练，模拟得到设计变量与零部件各失效模式可靠度和系统可靠度之间的显性函数表达式。
    ⑸ 将零部件的系统可靠度作为约束条件(或目标函数)进行优化设计，得到最终优化设计点。
2.2曝气机主轴应力分析
    BDY-4000型倒伞型叶轮表面曝气机如图1所示。主轴是其重要的组成部分。为了保证安全可靠性，按传统的设计方法往往把主轴直径设计得较粗，以致功率消耗大、用材多。

式中，ζ为轴径的制造误差系数。
    由于曝气机主轴主要承受扭矩作用，通常设计为等直径空心轴。基本随机参数向量为：

式中：D为主轴的外径(设计变量)；d为主轴的内径(设计变量)；M_n为传递扭矩；E为材料的弹性模量；G为材料的剪切弹性模量；S为材料的剪切强度。
    轴的截面尺寸D、d为设计变量。对等直径空心轴，要求重量最小，即要求截面积最小，按均值模型求解，目标函数定义为：
    　
    式中，α=d/D；ω_p为抗扭截面模量(mm³) ；σ_wp为考虑制造误差的抗扭截面模量(MPa)。
    根据应力-强度干涉理论，以应力极限状态表示的状态方程为:
   
式中，ω为抗弯截面模量(mm³)；σ_ω为考虑制造误差的抗弯截面模量(MPa)。
    应力极限状态表示的状态方程为:

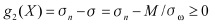
式中：σ_n为材料的许用弯曲应力；σ为主轴所受的弯曲应力；M 为主轴所受的弯矩(Nm)。
    (2) 刚度约束
    为保证轴的正常工作，设计时还应满足扭转刚度的要求，取传动轴的许用扭转角θ=2°。根据材料力学理论，传动轴扭转刚度对应的状态方程为：

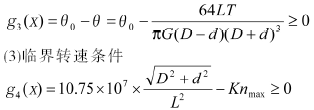
式中，n_max为轴的最高转速；K为临界转速的安全系数，其取值范围为=1.2～2.0。
    ⑷ 制造工艺条件

    g5(x)=D-d-2≥0

    g6(x)=85-D≥0

2.3 优化求解模型
    根据可靠性分析的简单界限理论，主轴系统可靠度的区间估计为^[2]：

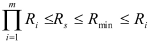
式中：m为各失效模式数，m=4；R_i为各失效模式可靠度；R_min为R_i的最小值；R_s为系统可靠度。
    在不考虑各失效模式之间的相关性，以各失效模式作为约束的条件下，进行优化设计^[3]，其优化设计模型为：

3 实例计算
    受企业委托，对其主产品BDY-4000型倒伞型叶轮表面曝气机搅拌轴进行可靠性优化设计。
    优化设计前原搅拌轴尺寸为：管外径D=159 mm，管内径d=100 mm。故选设计初值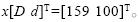
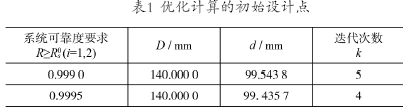
    允许误差ε=1×10^-4，得初始设计点如表1所示。

    考虑各失效模式之间的相关性，应用随机模拟神经网络方法，以轴的系统可靠度作为约束条件进行可靠性优化设计。在初始设计点附近的有限邻域内，对设计变量进行不同水平的组合(设计变量较少时，可以采用全面试验方法；设计变量较多时，可以采用正交设计或均匀设计方法以减少样本数)。本文采用全面试验方法，[D,d]^T分别在区间D=[136,140]和[96,100]均匀选取9个数据，组合得到81个样本数据。应用随机模拟方法进行可靠性分析，选取模拟次数为5 000次，计算得到对应的可靠度R=[R₁,R₂,R₃,R₄,R₅]^T，对设计变量样本数据x进行归一化处理为：

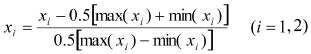
    将归一化处理后的x-R数据作为神经网络的训练样本。选用2-5-5的三层神经网络结构，x和R分别作为网络的输入和输出参数。传递函数均选用对数Sigmoid函数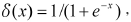各失效模式可靠度R₁、R₂、R₃、R₄和系统的可靠度R_s(记为R₅)为：

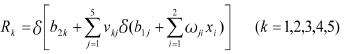
式中，ω_ji、v_kj为网络的连接权值； b_1i、b_2k为网络的连接阈值。
    选取学习速率η、动量系数k_f和训练误差△d_ij分别为0.6、0.8、10^-7，进行网络训练，获得训练后的网络参数。训练后的人工神经网络给出了设计变量x与可靠度R之间的显性函数表达式，以系统可靠度R_s作为约束条件进行优化设计。R⁰_s分别取0.99和0.995，优化后的最终设计点如表2所示。

    由Matlab仿真的误差如图2所示。

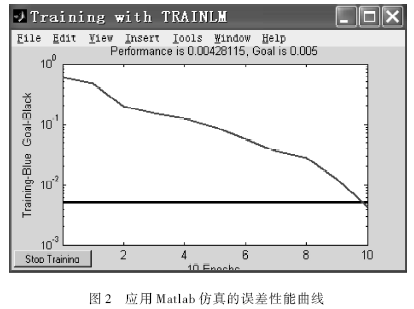
    从图2可以看出：应用人工神经网络，对BDY-4000型倒伞型叶轮表面曝气机搅拌轴进行可靠性优化设计，经过很短的训练时间就可以达到较高的计算精度，且预测值误差较小。
    本文通过对人工神经网络的学习研究，以搅拌轴重量为目标函数、分别以轴的强度与刚度临界转速以及制造工艺为约束条件，构造了曝气机搅拌轴优化设计数学模型。运用该数学模型，通过对BDY-4000型倒伞型叶轮表面曝气机搅拌轴可靠性优化设计，实例证明，本方法大功率曝气机搅拌轴尺寸优化效果明显。
参考文献
[1] NOLAN M K.  Optimal design of systems that evolve over time using neural networks [J].Proc. SPIE, 2007：6555-655514.
[2] GOH  A T C,  KULHAWY F H,  Reliability assessment of geotechnical serviceability state using neural networks [J]. GeoCongress, 2006.
[3] 芮延年. 现代设计方法及其应用[M].苏州：苏州大学出版社，2005.