摘  要: 级联空时格码方案可以有效地提高空时格码系统的性能。研究了两种级联空时格码方案：PC-STTC和ST-Turbo-TC。由于两种级联方案都使用了迭代译码方法，而外信息转移（EXIT）图是分析迭代译码性能的有利工具，主要分析比较了PC-STTC和ST-Turbo-TC的EXIT性能，比较了不同信噪比和编码多项式对于译码外信息转移特性的影响。研究结果显示，PC-STTC方案比ST-Turbo-TC方案有着更好的迭代收敛性能，同时给出了BER仿真图证明了EXIT图的分析结论。 

    关键词： EXIT图； 空时格码； 迭代译码； 收敛性

    基于互信息的外信息转移特性，通过软入软出的成员码译码器描述外信息的转移过程，这种方法已经被证明在低信噪比区域非常有效^[1]。在EXIT图中两个译码器之间外信息的转移轨道，即译码轨道可以清晰地表述译码算法的迭代收敛性能。 

    在空时处理信号中，为了进一步提高系统的带宽效率和可靠性，研究者提出了利用Turbo结构^[2]级联空时格码（STTC）^[3]方案。澳大利亚YUAN等人提出来了ST-Turbo-TC(Space Time Turbo Trellis Code)^[4,5]方案，在发送端经过删余等操作，该方案适用的天线数目及频谱效率与其成员码STTC是一样的。针对较多天线下STTC的应用，参考文献[6]提出了GSTTC方案，在接收端可以采用预测干扰抵消技术，但GSTTC的目标主要在于进一步提高STTC的频谱效率。另外一种PC-STTC方案^[7]，使得在发射天线数目较多情况下能在STTC的复杂度和性能之间取得折衷。 

    ST-Turbo-TC和PC-STTC方案在接收端进行初始估计后，都可以使用迭代原理方法进行译码，即外部信息在两个译码器之间能够被反复迭代交换。而且在使用同样的成员码时，两种方案几乎具有同样的实现复杂度^[7]。本文使用了EXIT图比较了这两种方案的收敛性能，并给出了BER仿真结果进一步证明了EXIT图表的分析结果。 

1 传输系统模型 

    考虑一个有N_T根发送天线和N_R根接收天线的MIMO通信系统，在时刻t，编码后的M-PSK符号指t时刻从第i个天线发出的符号。 

    在接收端，第j个接收天线接收到的信号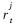是同一时刻经过衰落和高斯白噪声信道的各个发送天线的信号叠加: 

其中,H_i,j(t)是从第i个发送天线到第j个接收天线的信道的衰落因子;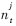是时刻t第j个接收天线上的噪声项，是均值为零、方差为σ²的复高斯随机变量。 

2 迭代译码器的外信息转移特性 

    无论是PC-STTC或ST-Turbo-TC方案都采用了迭代译码器原理。迭代译码的基本思想是利用代表决策正误的概率信息(称为软信息)在两个译码器之间进行反复式迭代译码。也可以说，迭代译码采用的是逐次逼近的方法。通常，使用迭代译码技术的编码器是由两个常规编码器级联而成，相应地，就会有两个译码器。与传统译码技术不同的是，除产生译码结果外，迭代译码器还要产生代表其所作判决正确性的概率信息(即软信息)，译码器1的输出信息被交织并反馈到译码器2，而译码器2产生的软信息又反馈给译码器1进行再一次的译码，整个译码过程就这样反复进行，直至达到一定的结果或达到指定的重复次数，再将最终的译码结果输出。在迭代译码过程中，每个译码器输出的软信息都作为先验概率提供给另一个译码器使用，正是这种先验概率的反复产生与反复使用，使得最终的译码性能得以不断提高。 

2.1 迭代译码器原理 

    以ST-Turbo-TC接收端为例介绍迭代译码器的算法，如图1所示。文中，每个译码器采用符号Log-MAP译码算法，即非二进制的译码算法。在二进制的译码中，通过计算每一信息位的对数似然比(LLR)得出每一位输出的概率，非二进制译码计算每个符号的对数后验概率，硬判决时，选择对数后验概率最大的符号输出。 

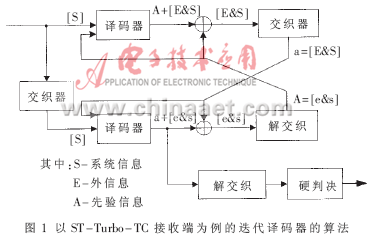
    Log-MAP译码器根据接收到的信号计算信息符号的对数似然比，译码器的软输出∧(c_n=k)由(2)式给出: 

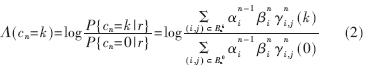
其中,k是发送符号集，r是接收到的序列，概率信息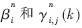可以由MAP算法计算得出。译码最后具有最大似然值的符号k作为硬判决被输出。 

    符号译码算法和二进制译码算法的区别在于交换的互信息不同，对于二进制的Turbo译码器，软输出可以分为三部分，即由另外一个译码器产生的先验信息(A)、由信息位产生的系统信息(S)和校验位产生的外信息(E)。 

外信息独立于先验信息和系统信息，在两个译码器之间进行交换。不同于二进制Turbo译码器，符号译码算法中信息和校验位是不能分开的，于是系统信息和外信息(E&S)也是不能分开的。因此，符号译码算法中两个成员码译码器中交换的是系统信息和外信息(E&S)。对于第一个译码器，系统信息和外信息的联合信息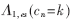可以由(3)式得到: 

    联合信息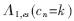被作为第二个译码器的先验信息进行输入，假设交织后的联合信息为则第二个译码器系统信息和外信息的联合信息可以由(4)式给出： 

    在下一次的迭代中，第二个译码器的联合信息被解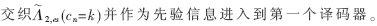 

2.2 外信息的转移特性 

    为了简单起见，采用通用的标识方法。译码器的先验信息A，可以表示为(5)式的形式，其中n_A为零均值方差为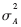的独立高斯随机变量，x是已知信息比特。 

    定义A的均值满足则条件概率密度函数如(6)式所示: 

    先验信息和原信息的互信息量可以由条件概率密度函数(6)式计算得出， 如(7)式所示。 

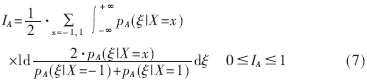
    外信息和原信息的互信息量I_E=I(X;E)同样可以由互信息计算得出，I_E可以看作是I_A和SNR的函数，外信息转移特性定义为如(8)式：  

    I_E=T(I_A,SNR)                                              (8) 

    为了计算T(I_A,SNR)，I_E的分布可以由Monte Carlo仿真决定(直方图)。 

3 计算机仿真结果 

    考照参考文献[4]中针对2×2天线的ST-Turbo-TC方案和参考文献[7]中的PC-STTC方案，采用参考文献[5]中提出的递归STTC作为成员码，其编码参数见表1，其中m代表编码寄存器数，n_T代表码字设计时参考的发送天线数，FFC指前向系数，FBC指反馈系数，4-PSK码字的频谱效率为2((b/s)/Hz)。

    图2给出了使用n_T为2的递归STTC作为成员码，且使用不同编码寄存器时PC-STTC和ST-Turbo-TC的外信息转移特性图，如参考文献[7]中所指出，这时PC-STTC和ST-Turbo-TC方案具有几乎等价的实现复杂度。图中I_A作为横坐标，I_E作为纵坐标，信噪比为2 dB，每一条线代表不同编码寄存器时的两种方案的外信息转移特性。可以看出，随着编码寄存器的增长，两种方案的译码迭代性都逐渐好转，但无论编码寄存器数是2或4，PC-STTC方案的迭代收敛性都优于ST-Turbo-TC方案。 

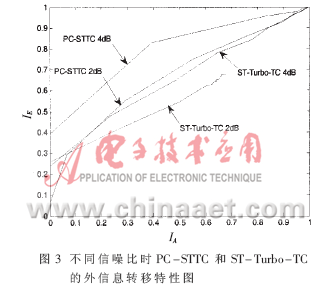
    图3给出了使用n_T为2，编码寄存器为2时PC-STTC和ST-Turbo-TC的外信息转移特性图。图中每一条线代表一个特定的信噪比。从图中可以看出，随着信噪比的增大，两种方案的译码迭代收敛性都明显好转，并且无论信噪比是2或4，PC-STTC方案的迭代收敛性都优于ST-Turbo-TC方案。 

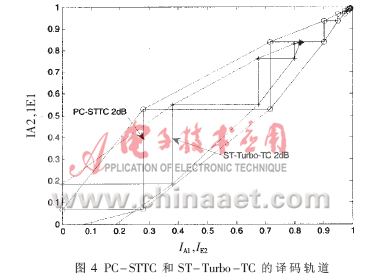
    为了更清楚地显示PC-STTC和ST-Turbo-TC方案的迭代译码过程，图4给出了编码寄存器为2，信噪比为2 dB时，PC-STTC和ST-Turbo-TC方案的迭代译码轨道。图中I_A和I_E分别代表先验信息和外信息，1和2代表译码器1和译码器2，第一个译码器的输出I_E1作为第二个译码器的输出I_A2。从图中可以看出，PC-STTC的迭代译码通道明显大于ST-Turbo-TC的译码通道。根据参考文献[1]中的理论，可以得出PC-STTC的迭代收敛性能明显好于ST-Turbo-TC的收敛性能的结论。 

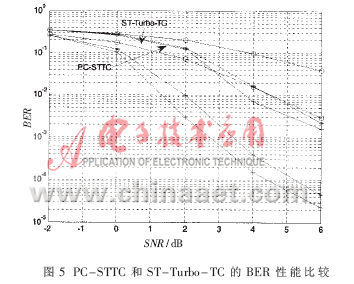
    EXIT可以反映出迭代译码的收敛性能，同时从另一方面揭示了译码误差性能的优劣。由上面的分析可以得出，PC-STTC方案比ST-Turbo-TC方案具有更好的迭代收敛性能，因此PC-STTC应该具有更好的误差性能。图5比较了PC-STTC和ST-Turbo-TC的BER性能，其中每一条线代表一个译码迭代次数(从1～3)。从图中可以看出，PC-STTC方案相对于ST-Turbo-TC方案，在BER为10^-3、译码迭代3次时，大约有超过4 dB的性能增益。考虑到PC-STTC和ST-Turbo-TC具有类似的复杂度，这种性能增益是相当可观的。 

    本文研究了两种级联空时格码方案，PC-STTC和ST-Turbo-TC的外信息转移性能。EXIT图显示，随着编码寄存器和信噪比的增长，两种方案的收敛性能都得到了好转。同时PC-STTC方案比ST-Turbo-TC方案有着更好的迭代收敛性能，并给出了BER仿真图证明了EXIT图的分析结论。 

参考文献 

[1] Stephan ten Brink. Convergence behavior of iteratively decoded parallel concatenated codes[J]. IEEE Trans.Communications, 2001, 49(10):1727-1737. 

[2] BERROU C, GLAVIEUX A, THITITMAJSHIMA P. Near shannon limit error-correcting coding and decoding: turbo codes (1)[C].  IEEE ICC’93, May 1993:1064-1070.  

[3] TAROKH V, SESHADRI N, CALDERBANK A R. Spacetime codes for high data rate wireless communications: performance criterion and code construction[J]. IEEE Trans Inform Theory, 1998,44(3):744-765. 

[4] HONG Y, YUAN J, CHEN Z, et al. Space-time turbo trellis codes for two, three and four transmit antennas[J].IEEE Trans.Vehicular Technology, 2004,53(2):318-328. 

[5] YUAN J, CHEN Z, VUCETIC B. et al. Performance and design of space-time coding in fading channels[J]. IEEE Trans. Commun., 2003,51:1991-1996. 

[6] DAI Y, LEI Z, SUN S. Iterative interference cancellation and ordered array processing for groupwise space time trellis coded(GSTTC) systems[C]. IEEE WCNC 2004:2323-2328. 

[7] YANG H, LI G, GUO Z, et al. Performance and EXIT analysis of parallel concatenated space time trellis codes. Accepted by Journal of System Engineering and Electronics.  

[8] DU J, LI Y. Parallel detection of space-time codes by predictive soft interference cancellation[C]. IEEE ICC 2004:2746-2750. 

[9] CHEN H, HAIMOVICH A M. Layered MIMO scheme with Antenna Grouping[C]. IEEE ICC 2004:478-482.