压电传感器
用于感应和激励的传感器" title="压电传感器">压电传感器应用延伸到了许多领域。本文主要介绍对一些物理强度的感应,即加速度、振动、振荡和压力,从传感器及其要求信号调节的角度来看其可以被认为是类似的。就加速度而言,传感器灵敏度通常被表示为一个与外力即加速度(大多数时候称作重力加速度g)成比例关系的电荷。然而,从严格物理意义上来讲,传感器输出一个实际由其变形/偏斜情况决定的电荷。
例如,图1显示了安装于顶部位置的一个传感器,与此同时底部正受到一个外力的拉拽,即Fext.在使用加速计的情况下,固定端(顶部)会粘附在要测量加速度的物体上,同时外力为粘附于另一端(底部)的质量的惯性,而这一端不断想要保持静止。就固定于顶端的参考坐标系而言(假设传感器充当的是一个弹簧,其具有很高的弹簧系数 K),偏斜x会形成一种反作用力:
Fint = Kx (1)
最终,质量(传感器偏斜)将会在下列情况下停止移动/改变:
Fint = Fext = Kx (2)
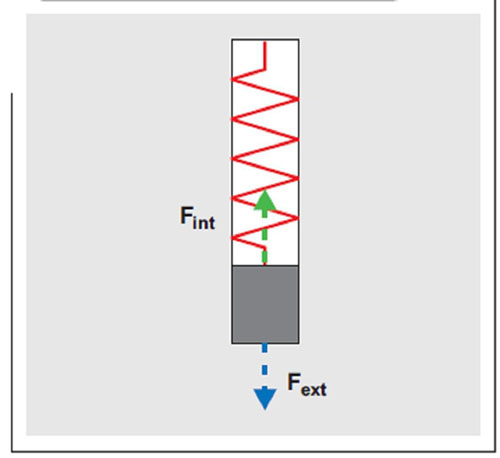
图1 加速度力作用下的传感器
由于电荷Q与偏斜成比例关系(一阶),而偏斜与力成比例关系,因此Q与力也成比例关系。施加一个 Fmax 最大值的正弦力,会形成一个Qmax最大值的正弦电荷。换句话说,当正弦力为最大值时,对来自传感器的电流求积分可得到Qmax.增加正弦波的频率,同时会增加电流;但是会更快地达到峰值,即保持积分(Qmax) 恒定。厂商会以传感器可用频率范围内Qmax与Fmax的比率来说明灵敏度规范。但是,由于传感器的机械性质,传感器实际上有谐振频率(可用频率范围以上),其中一个即使很小的振荡力都会产生相对较大的偏转,从而得到较大的输出振幅。
如果忽略谐振的影响,则我们可以将压电传感器一阶建模为一个与传感器寄生电容(此处称作Cd)并联的电流源,或者也可以将其建模为一个与Cd串联的电压源。该电压为存储电荷时在传感器阳极上看到的等效电压。但是,我们需要注意的是,就许多应用的仿真而言,第二种方法要更加简单一些。如前所述,电流与偏斜变化的速率成比例关系;例如,拿恒幅加速度的正弦AC曲线来说,电流生成器的振幅必须根据频率来改变。
最后,如果这种生成器需要代表实际物理信号,则可以使用变压器,如图2所示。本例中,我们建模了一个具有0.5pC/g灵敏度和500pF寄生电容的生成器。正弦波生成器每单位g输出1V以实现仿真。变压器在其次级线圈将它向下调节至 1mV.施加给C1(500 pF)的1mV摆动,将会如我们预计的那样在下一级注入 Q = VC = 0.5 pC.

图2 压电传感器模型
电荷放大器分析
图3显示了经典电荷放大器的基本原理,其可以用作一个信号调节电路。这种情况下,我们选择电流源模型,表明传感器主要为一种带高输出阻抗的器件。

图3 用于信号调节的电荷放大器
输入阻抗
信号调节电路必须具有非低的输入阻抗,以收集传感器的大部分电荷输出。因此,电荷放大器是理想的解决方案,因为只要放大器在这些信号频率下保持高增益,其输入便会让传感器信号出现虚拟接地。换句话说,如果传感器的任何电荷想要在传感器阳极(Cd)或者放大器输入寄生电容(Ca)上增大,在放大器输入端就会形成电压。通过拉或吸取相同量的负反馈网络电荷电流,即RFB和CFB,这种电压便立即得到了补偿。
增益
由于放大器的信号输入为虚拟接地,因此输入电流形成了一种输出电压摆动;并且高频增益由CFB的值设定(RFB 影响减小,在“带宽”部分后面再进行叙述)。请注意,电容越小,增益越大。增益的近似值为:

还需注意,电路增益根本上并非取决于传感器的电容(Cd),但最好还是注意该值对噪声的影响。
带宽
为了能够正确地对放大器进行偏置(为放大器输入偏置电流提供一个DC路径),一个反馈电阻(Rf) 是必需的。在更低频率下,反馈路径的电容电路变为开路,而反馈电阻变为主要电阻,从而有效降低增益。在较高频率下,电容电路的阻抗变得更小,从而有效消除电阻反馈通路的影响。对AC物理激励的最终电路响应(包括传感器的寄生电容)为高通滤波器的响应,其极频为:

相关信号带宽由应用决定,因此,降低电容增加增益的同时,也需要增加电阻来保持低极频。增加电阻会影响解决方案的其他方面。除影响噪声以外(在“噪声”部分详细介绍),电阻越高,实际实现就越难-难在寻找到现成的电阻,以及保证PCB的线迹到线迹寄生电阻大于RFB本身。如果电路规范允许使用几百兆欧量级的电阻,则表面贴装电阻马上就可以使用,并且不要求使用先进的布局技术(例如使用防护频带等)。
如前所述,限制电阻值增加的另一个因素是电路偏置。放大器的输入偏置电流通过该电阻形成输出偏置电压。通过选用具有低输入偏置电流的放大器,例如:FET 输入放大器等,可以最小化这种电压。只要反馈电阻器值低于 1GΩ,并且可以利用各级之间的AC耦合来滤波产生的偏置,那么这种放大器的输入偏置电流(一般低于 100pA)就应该没有问题。
请注意,由于保持高通滤波器低极频存在困难,因此在近DC应用中使用压电传感器也变得越来越困难(尽管传感器本身的漏电流非常小)。
尽管并非该放大级的组成部分,但也需要在某处添加一个低通滤波器,旨在降低电路对传感器谐振频率下无用信号的响应,同时降低相关频带的总数字化和混叠噪声。
噪声
最后,我们需要最大化信噪比(SNR)。在进行仿真以前进行简单的理论噪声分析会有所帮助。图4显示了电荷放大器的主噪声源。输出噪声谱密度可以表示为:
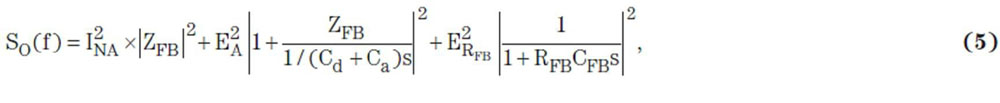
其中


图4 电荷放大器的噪声源
且s = 2πfj.方程式5为电荷放大器的经典噪声解决方案。相对于Cd,Ca一般非常小。因此,方程式5可以简化为:
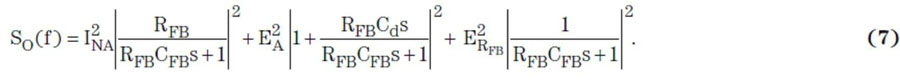
实际上,如果考虑使用高通滤波器极频以上频率,则可以进一步减小第二项:

我们可以使用几种方法来对各种趋势进行分析。极点(RFBCFBS + 1 项)可以被看作是恒定,因为增加RFB会要求降低CFB,反之亦然。从这个角度来看,增加 RFB会增加方程式8的三项。第一项相应的电压噪声会随RFB线性增加;第二项相应的电压噪声也会增加;第三项相应的电压噪声会随RFB的平方根增加,因为 ERFB=![]() ,其中 k=玻耳兹曼常数,而T=凯氏度温度。然而,由于CFB变得更小,增益会随RFB增加(参见方程式3)。随RFB增加而出现的信号增加,与方程式8中前两个噪声项的所有增加相似,但大于最后一个噪声项的增加,从而改善了总SNR.归根结底就是要尽可能多地增加RFB.需要注意的另一个趋势是从噪声角度来看,传感器的寄生电容越多,传感器就越不那么理想。
,其中 k=玻耳兹曼常数,而T=凯氏度温度。然而,由于CFB变得更小,增益会随RFB增加(参见方程式3)。随RFB增加而出现的信号增加,与方程式8中前两个噪声项的所有增加相似,但大于最后一个噪声项的增加,从而改善了总SNR.归根结底就是要尽可能多地增加RFB.需要注意的另一个趋势是从噪声角度来看,传感器的寄生电容越多,传感器就越不那么理想。
仿真结果
为了获得更为实际的电路实施,我们选用了TI的OPA337.这款放大器拥有低输入电压和低输入电流噪声(请参见图5),同时接受3V单极电源。图6显示了TI SPICE型仿真程序中这种电路的模型,即TINA-TI.
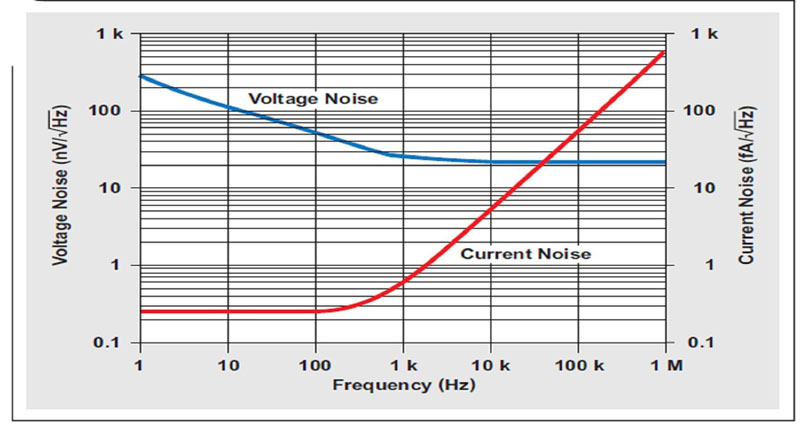
图5 OPA337的输入电压和输入电流噪声

图6 使用OPA337的电路TINA-TI模型
这种实施中,极点为0.86 Hz.我们可以在5 Hz下对方程式7进行分析,以仔细检查公式的精确度:
●在第一项中,如果INA ≈ 0.01 fA/√HZ ,且RFB =270MΩ,则该项对输出噪声的贡献值约为2.7 nV/ √HZ /5.85=0.5 nV/√HZ 。
●在第二项中,如果EA ≈ 60 nV/√HZ ,则这一项对输出噪声的贡献值约为 120nV /√HZ 。
●在第三项中,如果RFB = 270MΩ,则这一项对输出噪声的贡献值约为2μV/√HZ /5.85=340 nV /√HZ 。
把所有这三项二次方相加,得到约360 nV /√HZ ,其接近图7的仿真结果。但是,需要注意的是所用噪声值不同于图5所示数据表值。OPA337的TINA-TI 噪声模型并不精确,通过对图8所示简化电路进行仿真并得到图9所示结果(其应与图 5所示一样),可以证实这一点。

图7 图6所示模型的输出噪声仿真
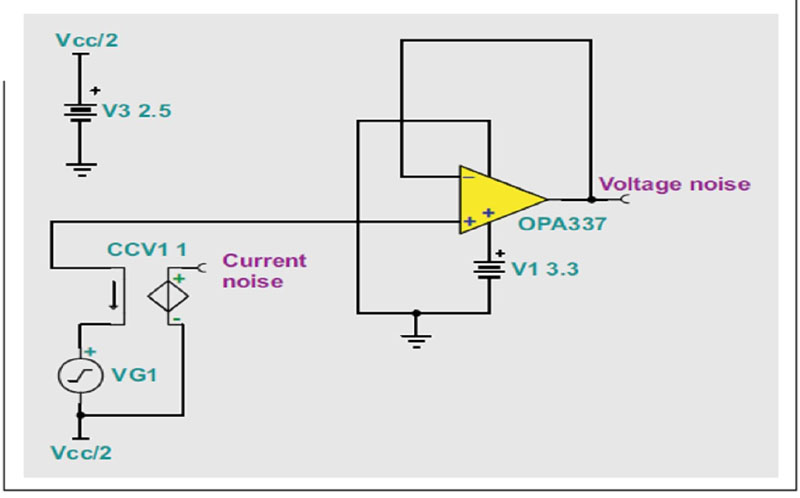
图8 放大器噪声分析的TINA-TI仿真电路
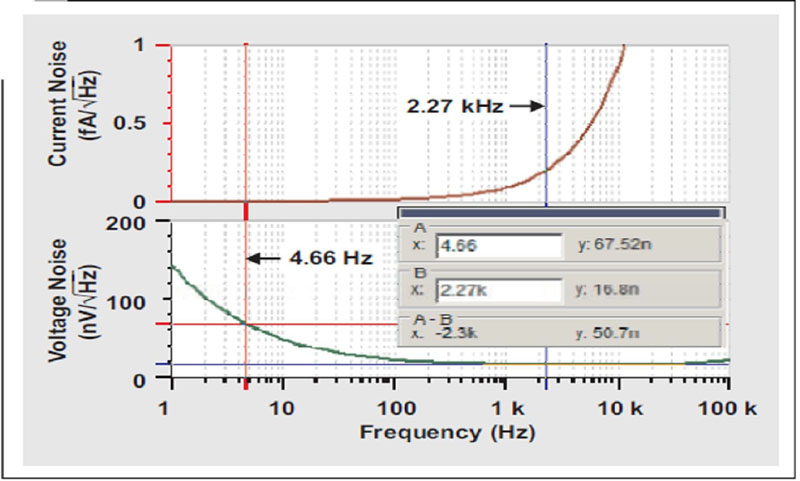
图9 图8所示电路的输出噪声仿真
这些结果突出了进行一次快速理论/工艺分析的重要性。该放大器电路并不准确,需要在TINA-TI中解释说明,以获得实际数值。我们可以在参考文献中找到完成这项工作的方法。一种稍微更简单的方法是,只需将噪声(图10中的Vnoise和Inoise)添加到图8所示电路,以对缺少项进行补偿。
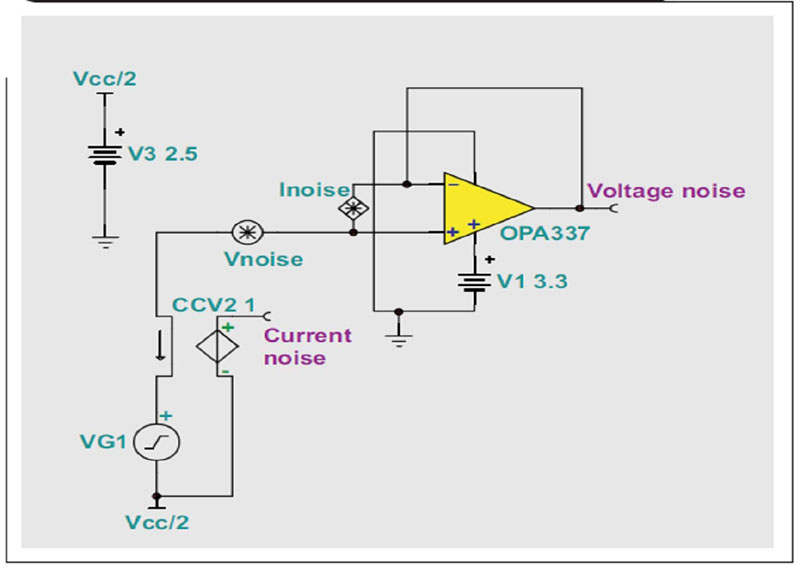
图10 添加至图8所示电路的噪声
尽管不是很完美,但图11所示结果看起来比图9所示结果要更加接近于规范。
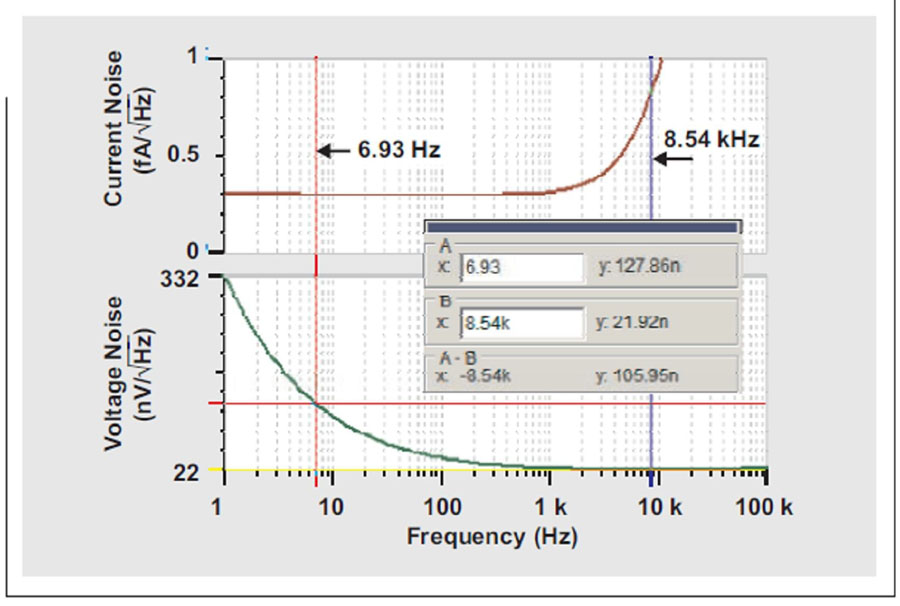
图11 图10所示电路的输出噪声仿真

图12 添加噪声源后图6电路的TINA-TI模型
利用图6所示原始电路,我们使用最初指定的一些噪声值,可以通过方程式7再次估算出5Hz的噪声。
● 在第一项中,如果INA≈0.3 fA/√HZ ,且RFB = 270MΩ,则该项对输出噪声的贡献值约为80 nV/√HZ /5.85=14nV/ √HZ 。
● 在第二项中,如果 EA ≈ 130nV/√HZ ,则这一项对输出噪声的贡献值约为 260 nV /√HZ 。
● 在第三项中,如果RFB = 270MΩ,则这一项对输出噪声的贡献值约为 (2 μV/ √HZ /5.85=340nV /√HZ 。
把所有这三项二次方相加,得到约为430 nV/√HZ ,如图13所示,其非常接近包括经校准噪声源的图12所示电路的仿真结果。
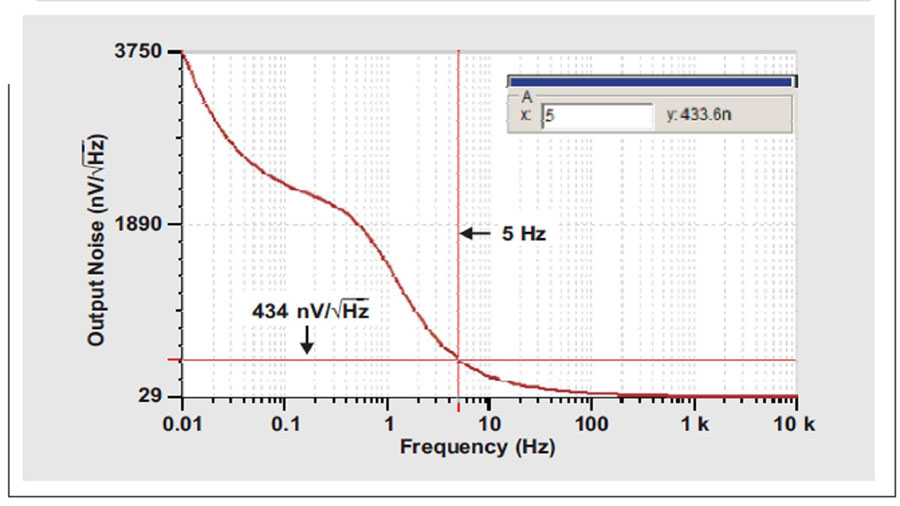
图13 图12 所示电路的输出噪声仿真
现在,请思考噪声变化与反馈电阻的对比结果。将方程式7第一项的RFB从270 MΩ改为540MΩ(且把CFB除以2,从680 pF降至340pF,目的是保持极频恒定),对输出参考噪声产生如下影响:
● 在第一项中,如果INA≈0.3 fA/√HZ ,且RFB =540MΩ,则该项对输出噪声的贡献值约为160nV/√HZ /5.85=28nV/√HZ 。
● 在第二项中,如果EA ≈ 130nV/ √HZ ,则这一项对输出噪声的贡献值约为320 nV/ √HZ 。
● 在第三项中,如果RFB = 540MΩ,则这一项对输出噪声的贡献值约为3 μV/√HZ /5.85=510 nV / √HZ 。
把所有这三项二次方相加,得到约为600nV/√HZ ,其再次接近仿真结果(参见图 14)。不出所料,输出噪声上升。然而,电阻加倍允许电容除以2,从而有效地使增益加倍(即输出信号加倍)。即使RFB为主导噪声源,且它的增加会使其噪声增加,我们也可以实现3dB的SNR改善,因为输出信号加倍远超出增加的噪声。
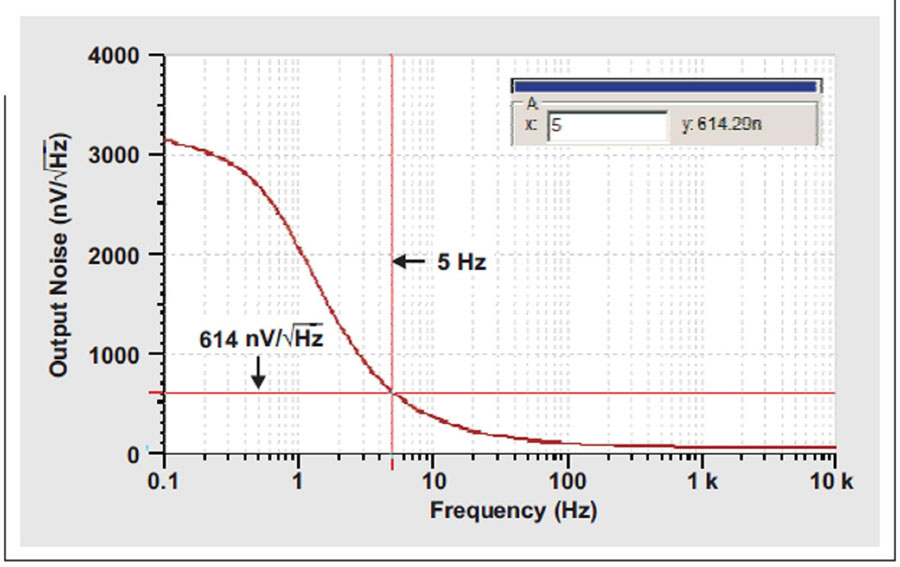
图14 RFB加倍而CFB 减半后图12所示电路的输出噪声仿真
其他实际问题
利用T型网络构建等效大电阻
当我们需要在反馈网络中使用非常大的电阻时,利用由许多更小、更易使用的元件构成的一个T型网络来构建这些大电阻,对我们很有吸引力(参见图15)。但我们一般不建议使用这种方法,因为T型网络会带来偏置和噪声大增益,从而一般会产生更糟糕的 SNR.
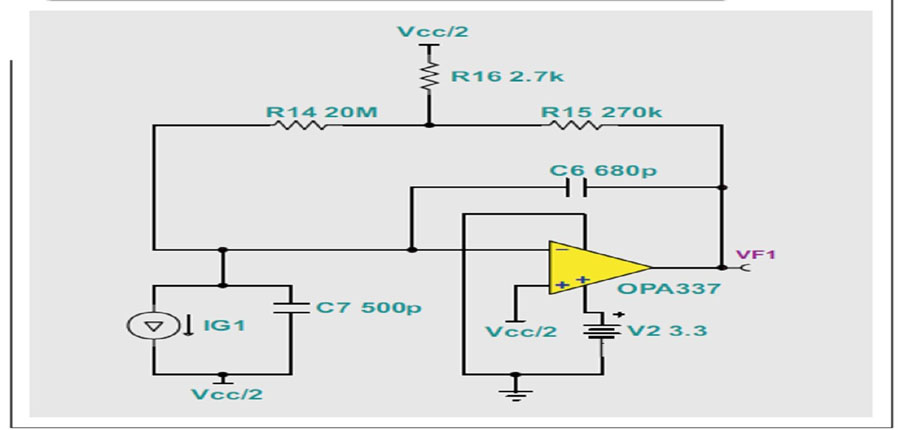
图15 T型网络反馈电路
使用差分输入
到目前为止,我们只字未提使用差分输入来降低噪声的好处。为了简单起见,我们以单端对建模放大器进行了分析,而图16显示的是一个带差分输入的改进配置结构。这种配置结构同时具有两个优势:
1、它固有两倍单端输入电路增益(电荷整合到C2和C4中),而噪声仅以平方根函数增加(即噪声源不相关)。
2、电荷放大器是一种非常敏感(高增益)的电路。图17表明任何输入干扰信号的电容耦合(此处为60Hz极板网栅)都会有效注入电流。就单端放大器而言,这意味着端子中的一个注入电流,而其他则接地;也就是说,放大器只会放大干扰信号。就差分输入来说,施加于两个端子的共模信号会相互抵消(假设寄生和反馈网络相同)。图18中,需要注意的是单端输入(蓝色轨迹)60Hz极板网栅的耦合结果,以及60Hz共模噪声如何被干扰信号(黄色轨迹)相互抵消的差分输入极大降低。本例中,为了方便理解,我们并没有尝试匹配超出10%组件容限的差动输入。

图16 使用差分输入的改进电路
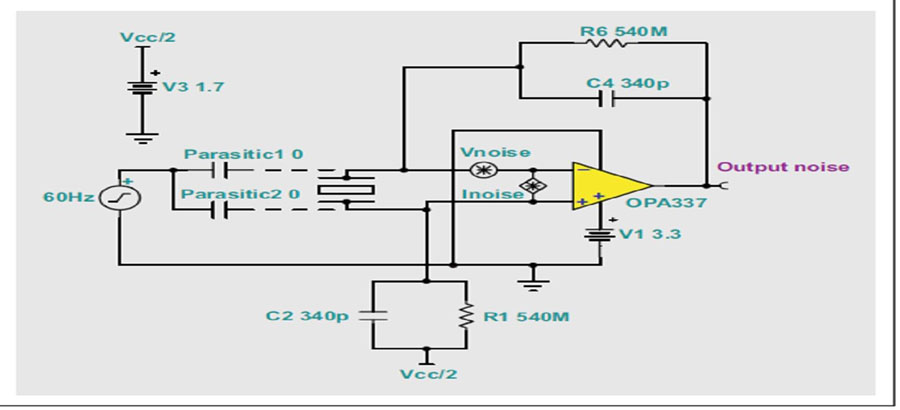
图17 60Hz共模噪声源对差分输入放大器影响情况模型

图18 差分放大器基本消除了共模噪声
结论
用户能够想到压电传感器,是因为这些器件可根据其失真情况输出电荷。就此而论,电荷放大器非常适合于这种应用。本文介绍了设计这种电路时需要牢记的一些一般性原则,例如:尽可能多地增加反馈电阻,密切注意放大器的输入偏置电流,以及使用一种差动结构等。本文还阐述了细化仿真以前进行理论分析的有效性。

