摘 要：设计了一种新的能量奖励机制，以提高微正则退火算法摆脱局部极值点的能力。在状态转移被拒绝后，通过比较两个能量参数的大小来启动奖励操作。奖励方式依旧为几何增长方式，但增长幅度改为一定区间内的线性调节。给出了一个采用改进算法的经典的单配送中心实例，它提高了微正则退火基本算法的优化效果，降低了搜索过程停滞在局部极值的概率，它搜索到的运输费用更贴近最佳解。
　　关键词：车辆路径问题；微正则退火算法；组合优化

　　配送车辆路径问题VRP（Vehicle Routing Problem）是指向一批客户配送物资，客户的位置和货物需求量已知，现有若干可供派送的车辆，车辆的运载能力给定，每辆车都从起点出发，完成若干客户点的运送任务后再回到起点，现寻求以最少的车辆数、最小的车辆总行程来完成货物配送任务。
　　车辆路径问题是物流配送中的关键决策问题，已有研究表明该问题属于NP难题^[1-2]。求解该问题有两类方法，一类是精确算法，另一类是启发式算法^[3-5]，后者力图在有限的时间内找到大规模问题的满意解，得到不少工程人员的关注。本文研究的微正则退火算法MA（Micro-canonical Annealing）也属于启发式算法的范畴，有关研究表明，该算法具有实施简单、运行速度快、优化效果出色等优点^[6]。笔者曾提出一种对该算法的改进思路，针对算法迭代后期的优化进程放缓问题，适时给予能量奖励策略，提高了在旅行推销员问题上的搜索性能。本文改进了这种能量奖励思想，将其用于配送路径的优化问题。实验研究发现，改进算法提高了最终解的质量，能够得到更低的运输费用。
1 配送车辆路径问题的数学模型
　　根据约束条件和目标函数的差异，车辆路径问题的数学模型可写成多种形式。最简单的情形是设计从一个位置出发，到多个不同位置的客户点的最优配送路径，即寻找一个运费最小的路径集合，并满足如下条件：
　　首先，每条配送路径上各个客户的需求量之和不超过汽车载货量。
　　其次，每个客户的需求必须满足，且只能由一辆汽车送货。
　　先作如下定义：i、j 为任意两个客户的标号，i、j∈N；N = { 1, 2,…, n}，n为客户的数目，标号0表示配送中心（即假定只有一个配送中心的情形）；k为配送车辆的标号；k∈k，k = {1, 2 , …, m}，m为车辆的数目；C_i,j为客户i、j 之间的距离；X_ijk为路径决策变量，当第k辆车从客户i驶向客户j时X_ijk为1，否则X_ijk为0；Y_ik为车辆与客户的配对参数，当车辆k服务客户i时取值为1，否则取0；w_j为客户j的货物需求量；D为车辆的最大载货量，C_min为最少总费用。可建立如下模型：
　　
　　式（1）为目标函数，使得总费用最小；式（2）表示每个客户都被访问且仅被访问一次；式（3）、（4）为每条巡回路径上的配送限制；式（5）为车辆的载货量限制。
2  微正则退火算法及改进策略
2.1 算法的基本原理
　　微正则退火与传统模拟退火的差异在于，它不再直接依赖系统温度，配分函数Z的形式为：
　　　　

　　式（6）中，E₀是初始能量值，K(P)是动量P在状态C下的能量，上式中没有出现温度参数。
　　在这一仿真方法中，假设热系统中存在一个具有能量交换能力的妖，它的作用类似式（6）中的动量P。这只妖可以在状态空间中随机行走，并通过改变热系统的状态变量达到调节系统能量的目的。仿真过程中，系统与妖的能量之和保持定值并且逐步降低，促使系统积累足够的能量以脱离亚稳态。令妖的能量为ED，ED为正数且初始值一般等于0。此时Z的形式为：
　　
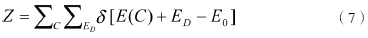
　　系统初始状态可以随机配置，妖在状态空间中每随机行走一步，就会尝试改变当前的系统状态，若此举能降低系统能量，则系统接收状态变迁。与此同时，系统释放的能量将会被妖吸收。当这种退火机制用于寻求目标函数最小值时，状态空间对应于自变量空间，系统能量对应于目标函数值。妖的能量变更可用如下公式表达：
　　
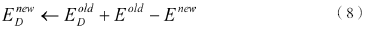
　　式中E^new、E^old分别表示新旧状态所对应的系统能量。为保证妖的能量总是正值，若妖的随机行走导致系统能量升高且升高幅度超过ED，该状态转移将被拒绝。另一方面，妖的能量ED也有上界约束M，该值随着迭代过程逐步减小。
2.2 能量奖励策略
　　妖的当前能量ED直接限制了系统能量回升的最大幅度，这一数值刻画出系统脱离亚稳态的能力大小。在算法后期，由于Emax的作用，ED总体处于下降趋势，劣状态被接受的概率非常低，若系统陷入一个比较深的能量局部极小状态，确定性的状态接受规则将使得系统几乎不能脱离该状态。
　　笔者曾考虑对妖的能量ED施加一种几何方式的能量奖励策略，在拒绝新状态后，适当增大ED的数值，以期逐步提高妖脱离局部极值的能力。具体操作方法是：对E_D实施比例为q的增幅，即E_D←E_D×(1＋q)，其中q值一般很小。在先前所做的实例仿真中发现，一种被称为无上界约束的能量奖励策略效果很小，这种方式在实施能量奖励后不检查ED是否超过E_max（当妖主动吸收能量后仍然要对ED做越界约束）。
3 改进微正则退火算法的实施
　　微正则退火算法用于组合优化时，算法的实施流程与传统模拟退火算法类似，具体体现在：第一，算法需要一个初始解，算法的主过程将在该初始解上执行领域变换；第二，算法的主流程也是双层循环结构，内循环按照退火策略更新状态。外循环是缩减妖的能量上界约束M（模拟退火中是降低温度）。
3.1 邻域变换
　　领域解的产生有两类常用方法，第一类是路径间优化，如路径插入法和路径交换法。第二类是路径内优化，如常用的二交换法，假设( i，i + 1) 和( j，j + 1) 是当前路径的两条边, 二交换后得到两条新边( i，j) 和(i+1，j +1)，且原路径中j和i+1节点之间的整段路径需要翻转，后续实验中使用了二交换方法。
3.2 退火策略
　　妖的能量上界约束M值在内循环中保持不变，内循环结束后该值将按比例缩减，即有M(i+1) =α_M(i)，M(i)表示内循环执行了i次后的M值，α为缩减系数。
    内循环的停止标准包括两种情形，一是在当前M下，已经尝试了U次循环；二是在当前M下，最好解成功已改进了L次，其中U与L是预定义的常数。
　　外循环在M低于预设值e，或找到指定解时即被终止，最后输出最终搜索结果。
3.3 改进的能量奖励策略
　　实施能量奖励策略时，需要做好两项决策，首先是奖励时机的选择，之前笔者曾设计过一种容忍机制，只在当前状态没改变累计达到一定次数后才实施奖励，这种方式操作起来比较简单，但容忍次数的设置没有可靠依据，只能通过经验预定。本文实验中通过能量差额比较的方法来启动能量奖励步骤，当未被接受的能量差额累计值超过某个数额时，妖将获得一次能量奖励。
　　为此，需再设定一个变量E_r和E_g。E_r以累加的方式记录连续的、未被接收的能量差额值。譬如当前领域变换得到的新状态将使得系统能量值提高12，而妖的能量值E_D=8，按照状态接收规则，新状态不被接受，此时E_r的数值将增加12。若新状态被接收，此时Er将被清零，使得能量奖励机制只在当前解连续多次没有改进时发挥作用。若新状态使得系统能量回升过大，E_r的累计操作将会被忽略，实际执行时，若未被接受的能量回升值超过了妖的最大能量上限M，该差额不被计入E_r。
　　E_g控制了奖励操作的阈值，可直接令E_g＝M，并随M的缩减而变化。在算法运行过程中，当E_r>E_g时，将执行能量奖励操作，随后Er被清零。
　　能量奖励策略的另一项决策是确定奖励幅度，在最初的算法改进方案中，执行固定比例的奖励（如奖励增幅q可设为0.01）。考虑到妖在算法运行前期获得额外奖励的需求并不强烈，而陷入停滞状态，往往是算法后期才表现出来，因此本文设计了一种新的奖励方法，增幅q将以线性增大的方式在预先选定的区间内变化（如0.005～0.05）。
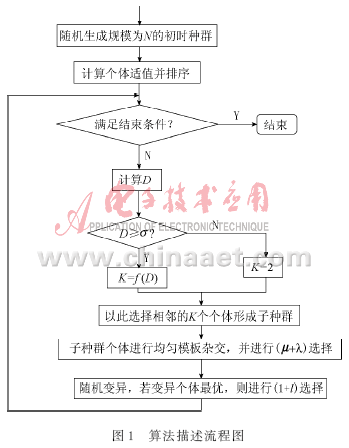
3.4 算法流程
　　（1）相关变量初始化操作，创建初始可行解，并释放能量E_D＝0的妖。
　　（2）外层循环控制，若M小于e则终止程序。
　　（3）更新M，按比例缩减；更新E_g与q。
　　（4）内循环控制，若满足3.2节所列条件，程序返回到步骤（2）。
　　（5）创建邻域解。
　　（6）若系统能量值降低或系统能量值增大幅度小于ED时均接受邻域解；更新Er；更新E_D。
　　（7）若领域状态被拒绝，则将此未被接收的能量增幅记入E_r中，并比较E_r与E_g，以决定是否实施能量奖励。
　　（8）返回步骤（4）。
4 实例分析
　　采用包含20个需求点的单配送中心实例来验证改进算法的效果^[4]。其中运输车辆的最大载货量D等于8。根据有关文献的建议，已有经验公式估计车辆总数^[7]，本文约定有6辆运输车。配送中心的坐标为（52，4），其他客户节点的坐标及需求量如表1所示。

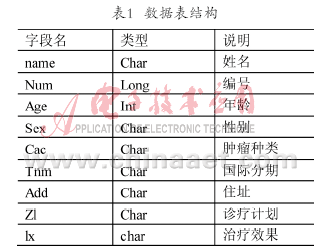
　　根据笔者之前对该实例的模拟经验，令初始M=100；α=0.95；U=100；L=30；e=0.01；q在0.005～0.05之间变化。在上述参数下，微正则退火基本算法的表现比较稳定。
　　表2展示了改进算法中能量奖励策略的效果。其中算法1指未进行任何改进的微正则退火基本算法；算法2施加了简单的能量奖励策略（即2.2节描述的方式）；算法3以能量差额比较的方式启动奖励策略，奖励幅度固定；算法4指以能量差额比较的方式启动奖励策略，奖励幅度线性变化。各组算法均以相同的初始解开始搜索，并对30次随机实验的结果进行统计。

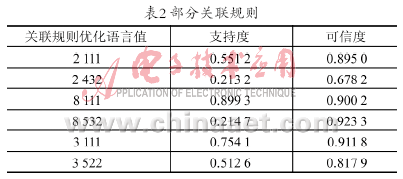
　　为了便于比较，以运输费用降到901作为算法搜索成功的标准，此运输费用是本实例一个较好的结果。表2中的第二列指最终找到这个满意解的次数。第三列指该算法的全部30次实验中，最终运输费用距离901的平均距离（费用差额值占901%），该比例越小，说明最终解越好。
　　对表2分析可见：首先，能量奖励策略是有效的，从一定程度上提高了算法搜索到指定满意解的能力。实施了能量奖励策略的三组算法，对于本实例的搜索成功次数都比基本算法要高。其次，利用能量差额比较来判定是否奖励的效果得到了验证，与简单的能量奖励策略相比，它的成功次数更大。再次，从表2的第三列可知，实施能量奖励策略后，多次实验的平均解要更列可知，实施能量奖励策略后，多次实验的平均解要更接近指定的满意解，而且本文提出的能量奖励实施策略进一步提高了微正则退火算法的搜索能力。
　　图1是上述实验中4种算法最低运输成本的变化轨迹。可以看出微正则退火基本算法在最开始阶段的下降速度很快，但到后期不如其他算法。根据能量奖励策略的特点可知，它使得整个搜索过程更为平缓一些，前期目标函数值下降稍慢，这从一定程度上消弱了微正则退火算法本身的快速优化优势，但从图1可发现，施加了改进的能量奖励策略后，对上述问题有了明显的改善。