当前，非接触式测量已经逐渐取代接触式测量，成为测量发展的方向。而在各种各样的非接触式测量方法中，光纤干涉投射技术测量物体表面形貌的方法，由于其光路具有柔软、形状可变、传输距离远、抗干扰能力强等优点，得到了越来越广泛的应用，尤其在各种有强电磁干扰、易燃易爆等恶劣环境中，光纤干涉投射测量技术更是有着很高的应用价值。
    在光纤干涉投射技术中，裸露在空气中的光纤容易受到温度、振动的影响，使臂长差发生变化，进而产生光相位的变化，导致干涉条纹漂移，从而影响到测量的精度[1]。交流相位跟踪零差补偿技术（PTAC）是实现光纤相位变化检测和误差补偿的一种关键技术[2]，其中涉及信号解调和相位求解，求解反正弦是相位求解的一种主要方法[2]。在FPGA中，传统的求解反正弦函数的主要方法是查找表法[3]，查找表数据量的大小和精度紧密相关，在高精度下，查找表法需要大量存储单元，另外也需要校正算法来计算未计入表中的点，这样就对处理器资源提出很高的要求。
    针对传统反正弦函数求解方法的缺点，本文采用CORDIC算法求解反正弦值，得到光相位变化并在FPGA中设计了CORDIC算法实现的流水线结构，从而达到了对光相位变化的实时检测。同时，提出采用查找表配合抛物线插值校正算法解决CORDIC算法在运算中存在的“死区”问题。通过实验验证该了方法的可行性。
1 系统结构
    光纤干涉投射系统由激光器、聚焦透镜和3 dB耦合器等组成。激光器发出的激光经过聚焦透镜耦合到光纤，经3 dB耦合器分光后由两光纤臂输出。两光纤输出端可被看作是杨氏双孔干涉中的两个小孔，其输出光由同一点光源发出，频率相同，具有恒定的相位差，满足杨氏双孔干涉条件，从而在输出端产生干涉条纹。在实际测量中，温度、振动的影响使光纤发生臂长差变化，从而使光相位发生变化，导致干涉条纹漂移。为解决这一问题，通过PTAC对光相位进行调制解调得到光相位变化信息并对相位误差进行补偿。
    如图1所示，光纤干涉投射交流相位跟踪零差补偿系统由激光器、聚焦透镜、3 dB耦合器、PZT和信号调理等部分组成。两输出臂分别缠绕在两个PZT上，一路作为信号臂对光相位进行调制，另一路用作控制和补偿。两条输出臂投射端面存在反射，反射的光返回到3 dB耦合器中发生干涉，构成马赫-泽德干涉仪[4]，干涉的光由光电探测器PD接收。信号臂反射回耦合器的光包含光相位调制信息，同时也存在着由环境影响产生的光相位变化信息。两束反射光在耦合器中发生干涉，则光相位调制信息转化为光强变化，再由光电探测器将光强变化转化为电信号。

 
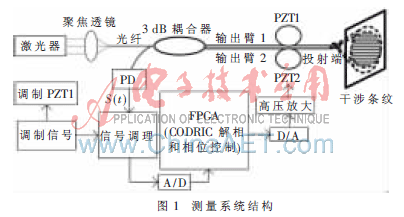
    经过AD转换后，输入FPGA进行计算，通过求解反正弦求出?琢。改变驱动器的直流偏置，即改变待测镜和参考镜的相位差?琢。再经过数模转换、高压放大，通过控制PZT2调整另一输出臂的长度，使两光纤臂相位差保持为一正弦函数，消除温度振动等环境因素带来的影响。
2 反正弦算法实现
2.1 反正弦算法原理
    基于CORDIC算法计算反正弦。数字信号处理中常常会遇到求解超越函数的问题，如求解矢量旋转、反三角函数运算、双曲函数等，CORDIC是为了这些问题而提出的[5]。CORDIC基本思想是用一组确定的角度不断摆偏去逼近所求的角度，而这一组角度与运算基数（2i）有关。在硬件电路中，CORDIC运算可以只通过加减操作和移位操作实现，大大节约了资源。CORDIC算法可由式(3)、(4)、(5)、(6)给出[6]。其中，(xi，yi)是矢量的坐标，zi为剩余未旋转的角度。

2.2 反正弦程序设计
2.2.1 字长设计
    输入值范围为[-1，1]，输入FPGA的初值c为12位。选第一位为符号位，第二位为整数位，后10位为小数位。在FPGA中，使用浮点形式计算小数比较复杂，因此，将小数部分左移10位，化成定点形式运算。CORDIC的计算次数取决于xi、yi的小数位数。如式(8)，用yi与输入初值c比较，如果yi的小数位为10位，则最多进行10次CORDIC计算，精度很难保证。因此，设计xi、yi的小数位为22位，在c后面补0，补足22位小数位，则最多可进行22次CORDIC计算。因为z的值域范围为[-1.570 8 rad，1.570 8 rad]，将z设计成25位，z[24]为符号位，z[23:22]为整数位，z[21:0]为小数位。
2.2.2 实现结构的设计
    在FPGA中，CORDIC的实现结构可以选择迭代结构或流水线结构。迭代结构是直接由公式写出循环语句，处理完当前数据才可以处理下一个数据，缺点是效率低。本设计采用流水线结构，流水线结构在数据处理的同时，还能继续输入和处理后续数据，提高了数据吞吐率。此外，设计中采用前端数据处理加22级CORDIC计算加后端处理，第一个数据需要24个时钟周期处理完毕，之后每个周期都可以输出一个处理结果，可以显著提高数据处理速度。
2.2.3 CORDIC结构
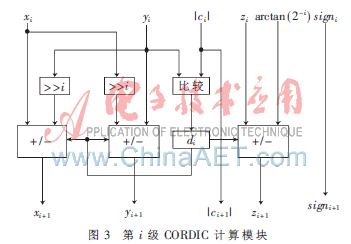
    本设计总共有22级CORDIC计算模块，第i级CORDIC计算模块如图3所示。yi与|ci|比较，决定di的值，再根据式(7)来计算xi+1、yi+1、zi+1，同时传递输入值的符号位，在流水线的后端处理模块处理。若输入c[11]为1，则结果为-arcsinc；若输入c[11]为0，则结果为arcsinc。

3 算法校正
    输入数据范围为[-1，1]，将计算结果与真实结果比较，得到误差分布如图4所示。

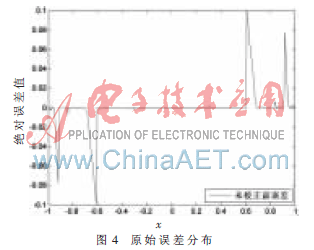
    由图4可见，在横坐标绝对值为0.6、0.8、0.9附近出现较大误差，最大误差达到10-1数量级。CORDIC算法使用的是一种数值计算逼近的思想，增减的步长值是离散的，为arctan(2i)。在横坐标绝对值为0.3、0.6、0.8、0.9附近，CORDIC计算存在“死区”。本文采用查找表和抛物线插值校正，在误差值较大的区间[c1，c3]，令：
  
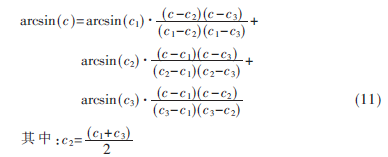
    在前端数据处理中判断输入值是否在需要校正的区间，若在则进行抛物线插值校正。用少量查找表存储校正区间端点的反正弦值和分母的比值。选用FPGA为32 bit，在其中设计乘法运算时，乘数和被乘数最高为16 bit才不会使数据溢出。在所有抛物线插值校正系数中，区间[0.95，0.96]上抛物线插值校正的一次项系数最大为22.108 9。因此选择高5位为整数位，低11位为小数位进行运算。
4 实验与仿真
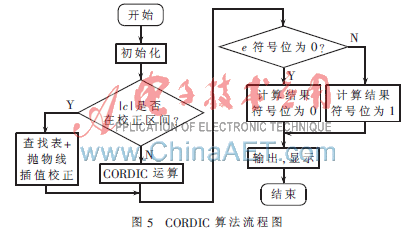
    CORDIC程序流程图如图5所示，初始化之后，先判断输入值c是否在需要校正的区间。若是，则进入抛物线插值校正运算；否则进行CORDIC运算，使x0=1/An，y0=0，z0=0。CORDIC运算计算出一个小数的反正弦值需要24个时钟周期，为了保证流水线的机能，当输入值c在需要校正的区间时，插值计算后的数据在CORDIC运算模块中直接传输。计算出反正弦值后，判断输入值c的符号位，如果是0，则c为正数，反正弦值也为正数；如果是1，则c为负数，反正弦值也为负数。

    仿真软件采用ModelSim SE PLUS 6.2b。输入的c值范围为[-1，1]，存放在ModelSim的测试激励文件中。处理一个数据需要24个时钟周期，之后每个周期都能输出一个数据，如图6所示。

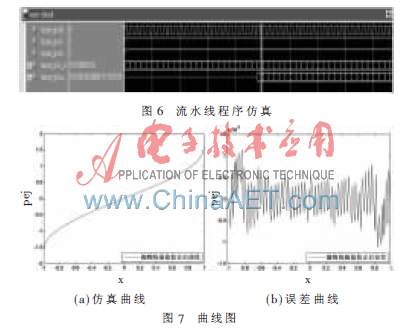
    将仿真后的数据导入Matlab得到反正弦仿真曲线，如图7(a)所示，并与理想值对比，得到如图7(b)所示误差曲线，CORDIC计算部分弧度值精度达到10-4数量级，经过校正的部分，误差从10-1数量级降到10-4数量级。
    本设计采用流水线结构，提高了数据吞吐率。仿真实验表明，光相位的误差精度达到10-4数量级，精度较高，且具有较高的运算速度，适合大数据量高速处理。
参考文献
[1] Duan FaJie，Zhang Cong，Zhang Chao，et al.Fourier transform profilometry based on fiber-optic interferometric projection[C]，2009 2nd International Congress on Image and Signal Processing.2009.
[2] 李超．迈克尔逊型全光纤加速度地震检波器理论与实验研究[D].天津：天津大学，2007.
[3] 付雷，陈淑芬，孟彦斌．数字式开环单模光纤陀螺中求arcsine的查表和线性插值法[J]．北京理工大学学报，2003，23(4)：499-502.
[4] 孟克．光纤干涉测量技术[M]．哈尔滨：哈尔滨工程大学出版社，2008：67-74.
[5] RAY A.A survey of CORDIC algorithms for FPGA based  computers[C].Proceeding.ACM/SIGDA Conference，1998：191-200.
[6] CHANG Y K，Swartzlander.An analysis of the CORDIC algorithm for direct digital frequency synthesis[C].In：IEEE International Conference on ASAP.California，USA：IEEE  Press，2002：111-119.