摘 要: 提出一种基于概率与信息熵理论的实值属性离散化方法,综合考虑了各对合并区间之间的差异性;该方法利用信息熵衡量相邻区间的相似性,同时考虑离散区间大小和区间类别数对学习精度的影响,并通过概率的方法得到了这两个因素的衡量标准。仿真结果表明,新方法对See5/C5.0分类器有较好的分类学习能力,并在肿瘤诊断中得到了很好的应用。
关键词: 离散化;数据挖掘;概率;信息熵
连续属性离散化是数据挖掘和机器学习的重要预处理步骤,直接影响到机器学习的效果。在分类算法中,对训练样本集进行离散化具有两重意义:一方面可以有效降低学习算法的复杂度,加快学习速度,提高学习精度;另一方面可以简化、归纳获得的知识,提高分类结果的可理解性。很多离散化方法的提出,主要分为以下两种类型[1]:(1)自底向上和自顶向下的离散化方法。自底向上离散化方法是以每个属性值为一个区间,然后迭代地合并相邻区间;自顶向下离散化方法是把整个属性的值域视为一个区间,递归地向该区间中添加断点。(2)有监督和无监督离散化方法。有监督方法使用决策类信息进行离散化,如Ent-MDLP[2]、CAIM[3]和Chi2-based[4-5]等算法。Ent-MDLP使用熵的理论来评价候选断点,选择使得整体熵值最小的断点作为最终断点,并且通过最小描述长度原则来确定离散区间数;CAIM是一种自顶向下离散化方法,该方法依据类与属性间的关联度,提出一种启发式离散化标准,计算当前状态的标准值来判别当前断点是否应该被加入断点集合中。自底向上的Chi2-based离散化算法使用卡方统计来确定当前相邻区间是否被合并,并采用显著性水平值逐渐降低的方法检验系统的不一致率,确定离散化进程是否终止。然而,Chi2-based方法在衡量区间差异时没有考虑区间大小和区间类别数对离散化结果的影响,可能会导致学习精度的降低;而无监督离散化方法则不考虑类的信息。传统的无监督离散化方法包括EWD(Equal Width Discretization)和EFD(Equal Frequency Discretization),这两个算法实现简单且计算消耗低,但结果往往难以满足预计的要求。
本文提出一种基于概率与信息熵理论的实值属性离散化方法PIE(Probability and Information Entropy),综合考虑了各对合并区间之间的差异性,利用信息熵衡量相邻区间的相似性,同时考虑离散区间大小和区间类别数对分类能力的影响,并通过概率的方法得到了这两个因素的衡量指标。实验结果表明,PIE显著地提高了See5/C5.0分类器分类学习精度,并在乳腺肿瘤诊断中得到了很好的应用。
1 PIE离散化
离散化问题描述如下:对于m个连续属性的数据集,样本点个数为N,决策类别数为S,数据集中任意一个连续属性为a,可以将连续属性的值域离散成I个区间:
P:{[d0,d1],[d1,d2],…,[dI-1,dI]}
其中,d0是连续属性A的最小值,dI是a的最大值,属性a的值按升序进行排列,{d0,d1,d2,…,dI-1,dI}为离散过程中的断点集合。属性a的每个值都可以划分到离散的I个区间的某一个区间中。

对于一个连续属性的各对相邻区间,它们对应的类分布是不同的,类分布最相似的区间应该先被合并。事实上,从信息通信的角度考虑,区间在合并前与合并后需要转换信息量,转换的信息量越小,说明两个区间对应的类分布越相似,它们应该被合并,反之亦然。由于相邻两区间的样本数为M,需要转换M次,因此,用M×[H(I)-H(I1,I2)]作为区间相似性的衡量标准。
为了更好地衡量各对合并区间之间的差异性,仅考虑类分布的相似性是不够的,还需要考虑离散区间大小和区间中类别数对离散化结果的影响,进而会影响到分类器的学习精度。通过概率的方法可获得两个因素的衡量标准,对于任意连续属性,每一对相邻区间(I1和I2)的样本数是不同的,可视为变量{Mi},则p({Mi+})代表两个区间样本数的集合可能性,即:

2 仿真结果
2.1 UCI数据集实验结果
为了评价PIE的性能,采用了UCI机器学习数据库[7]中的10个数据集,见表1所示。该数据集是数据挖掘等实验常用的数据,其中包括两个大的数据集Page-blocks和Letter。PIE方法与以下几种方法进行了比较:传统的无监督离散化方法EFD;基于熵的最小描述长度离散化方法Ent-MDLP;流行的自顶向下离散化方法CAIM;经典的自底向上离散化方法Chi2。
10个数据集分别采用上面的离散化方法进行离散数据,使用Weka数据挖掘工具进行实验,采用See5分类器对离散后的数据进行分类预测。采用10折交叉验证的方法,将数据集分成10等份,分别将其中9份作为训练集,剩下1份作为测试集,重复10次取平均值,对平均学习精度统计进行对比,见表2所示。
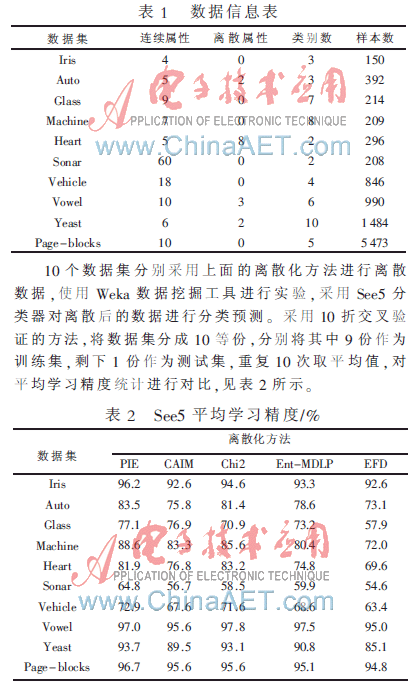
从表2中可以看出,除了Heart和Vowel数据集,本文提出的PIE离散化方法的See5平均学习精度均有所上升,这正是离散化方法期望得到的结果,由此充分显示了PIE算法的优势。而对于CAIM、Ent-MDLP和EFD三种离散化方法均则未引入不一致衡量标准,即它们没有对数据的有效性进行控制,在离散化过程中丢失了大量的信息,导致分类预测的精度比Chi2和PIE方法平均低很多。
2.2 PIE在乳腺肿瘤诊断上的效用
乳腺肿瘤诊断的实验数据来自于UCI机器学习数据库中的Breast Cancer Wisconsin数据集,将Breast Cancer Wisconsin删掉属性值不全的病例样本,剩下683个病例样本,病理检测有9项(Clump Thickness、Uniformity of Cell Size、Uniformity of Cell Shape、 Marginal Adhension、Single Epithelial Cell Size、Bare Nuclei、Bland Chromatin、Normal Nucleoli、Mitoses),即9个属性,每个属性取值范围[1,10],病情状况分为两类:一类表示肿瘤为恶性,另一类表示肿瘤为良性。这样,每个样本有9个连续条件属性,1个决策属性,选取样本的80%作为训练集,20%作为测试集。
将Breast Cancer Wisconsin用本文所提出的PIE算法进行离散化,然后分别使用See5和PIE+See5对离散前和离散后的数据进行分类预测,结果见表3。

从表3中可以明显看出,未经过离散化处理的BCW病例数据集进行See5分类预测的测试准确度为92.55%,而PIE+See5方法的测试准确度为99.27%,比未被离散化的进行See5预测精度高出6.72%,相当于每1 000个患者中就多出约67个患者可以被准确地诊断出肿瘤为良性或是恶性,对患者及时治疗有很大帮助。
在BCW数据被离散化后,其病理指标被删去了三项:Uniformity of Cell Shape(细胞形状均匀度)、Bland Chromatin(平淡的染色质)、Mitoses,可以只考虑其他六项,简化了信息系统,减轻了医生的工作量。另外,利用PIE+See5方法离散后不同样本占样本总数比例只有44.36%,删除冗余的病例样本后,只剩余了303个病例样本,从而使原来的病例样本空间在横向和纵向上都得到了降维,可以得到更加稳固的训练模型,在医学数据挖掘中具有良好的发展前景。
连续属性离散化方法的研究对数据挖掘与机器学习领域的研究与应用具有重要的作用。本文提出一种基于概率与信息熵理论的实值属性离散化方法,综合考虑了各对合并区间之间的差异性,能够更合理准确地离散化,该方法为该领域提供了新思路,具有一定应用价值意义。
参考文献
[1] DOUGHERTY J, KOHAVI R, SAHAMI M. Supervised and unsupervised discretization of continuous feature[C]. Proceedings of the 12th International Conference of Machine learning. San Francisco: Morgan Kaufmann, 1995.
[2] FAYYAD U, IRANI K. Multi-interval discretization of continuous-valued attributes for classification learning[C]. Proceedings of the 13th International Joint Conference on Artificial Intelligence. San Mateo, CA: Morgan Kaufmann, 1993.
[3] KURGAN L A, CIOS K J. CAIM discretization algorithm[J]. IEEE Transactions on Knowledge and Data Engineering,2004, 16(2): 145–153.
[4] LIU H, SETIONO R. Feature selection via discretization[J]. IEEE Transactions on Knowledge and Data Engineering,1997, 9(4): 642-645.
[5] CHAO T S, JYH H H. An extended chi2 algorithm for discretization of real value attributes[J]. IEEE Transactions Knowledge and Data Engineering, 2005,17(3):437-441.
[6] PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982,11(5):341-356.
[7] HETTICH S, BAY S D. The UCI KDD Archive [DB/OL]. http://kdd.ics.uci.edu/, 1999.

