摘  要： 在IDEA算法的基础上，分析其存在的弱密钥，其加密过程也决定了相同的明文必定加密成相同的密文，容易暴露明文的统计学特性。设计了基于IDEA 算法的加密算法X_IDEA，较好地解决了IDEA算法的弱密钥问题。X_IDEA算法的加密过程中嵌套IDEA算法，特殊的加密过程设计使得其安全性和抗攻击能力较IDEA算法更强。
关键词： IDEA算法；X_IDEA 算法；IDEA_KEY算法；加密

1 IDEA算法简述
　IDEA(Internation Data Encryption Algorithm)数据加密算法是由中国学者来学嘉博士和著名的密码专家James L.Massey于1990年联合提出的。IDEA是对64 bit大小的数据块加密的分组加密算法，密钥长度为128 bit，是基于“相异代数群上的混合运算”的设计思想，其算法用硬件和软件实现都很容易，而且比DES实现快。IDEA算法既可用于加密，又可用于解密。
　IDEA也被认为是目前世界上最好最安全的分组密码算法，且对计算机功能要求不高。IDEA的128 bit密钥长度，相对较长，但加密强度高。在穷举攻击的情况下，IDEA需要经过2128次加密才能恢复出密钥，假设芯片每秒能检测100亿个密钥，需要10年。IEDA被认为仅循环4次即可抵制差分密码分析，对IDEA算法也不起作用，随机选择密钥基本没有危险，故其安全性较高。IDEA算法基于一些可靠的基础理论，软件实现的IDEA比DES快2倍。
　IDEA算法是由八个相似圈外加一个输出变换组成的循环密码。圈函数的模块是模216+1乘法。模216加法和按位XOR。IDEA有一个128 bit的总密钥和以64 bit为块的加密数据。  
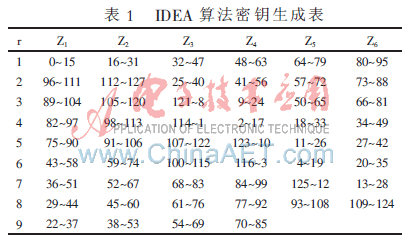
除密钥调度之外，IDEA解密过程与加密过程相同。加密圈密钥是总密钥的16 bit子串，如表1所示。解密圈密钥能从加密圈密钥中导出。
1.1 IDEA明文长度
　在IDEA算法中，加密前对明文的处理方法是：依次将明文分解成64 bit的数据块，最后一个数据块如果不足64 bit则进行补位处理。明文的长度固定且比较短只有64 bit，因此，在对格式化数据进行明文分组时必然存在较多的相似明文分组，并且这些相似的明文分组往往是连续排列的。IDEA算法在进行加密时当前被加密明文分组与其他明文分组没有任何关系，加密密钥和加密流程也完全相同，所以在对格式化数据进行加密时，明文中相同的部分会被加密成相同的密文，明文的数据格式及某些统计学特性也将暴露无遗，降低了明文的保密性[1]。
1.2 IDEA的弱密钥
　IDEA算法一次完整的加密运算需要52个(832 bit)子密钥。这52个16 bit的子密钥都是由一个128 bit的加密密钥产生的。生成的过程如下：
　将128 bit分成8份，每份16 bit，相当于Z1~Z8的子密钥。Z1的16 bit对应加密密钥中的最高阶的16 bit。而Z8的16 bit对应加密密钥中的最低阶的16 bit。将加密密钥循环左移25 bit之后，同样可得到另外8个子密钥Z9~Z16。重复同样的步骤，依次循环即可得到52个子密钥(详见表1)。

　参考文献[2]中指出了IDEA算法中存在弱密钥的问题。在标准IDEA算法产生的密钥中，其中的一类(223个)密钥存在一个线性因子；另一类(235个)具有一个概率为1的环形阶；还有一类(251个)，可以解一组含有12个变量的16个非线性布尔等式测试出所使用的密钥是否属于这一类，若使用的密钥属于这一类，则就有高效破译这一密钥的方法。
　在参考文献[3]中，作者就是通过这些不断重复出现的128 bit原始密钥，通过这些特别选定的密文可以测试和观察出密钥所含的线性因子，通过8轮的迭代，密钥中的线性因子也逐渐增多，可推算出26~40 bit，72~83 bit和99~122 bit密钥的值。按照IDEA算法设计者的思路其密钥空间应该为2128，但现有251个为弱密钥，所以其真实密钥空间应该为277。
2 X_IDEA算法设计
2.1 明文处理
　在X-IDEA算法中，不再按IDEA算法中那样依次将明文分解成64 bit的数据分组。加密前先对明文进行重组，加大明文的初始分组长度，进行第一次等长分组后判断各分组的长度是不是64的整数倍，如果不是则对明文进行补位(特殊字符)，使明文的长度达到64的整数倍；如果明文的长度是64的整数倍，则不做补位处理。最后加密前再将每一组明文分解成若干64 bit的明文分组，此为第二次分组，所以加密的明文分组仍为64 bit。
　明文重组过程如图1所示。

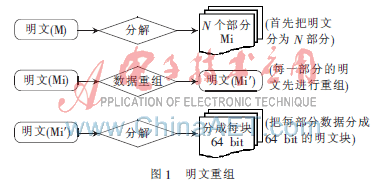
　在图1明文重组的第二步中，实际上绝大多数情况下需要对数据分组进行补位处理，对于格式化的明文文件，其明文统计学特性能得到部分的隐藏。实际上，在进行明文重组时，也可以将第一次分组所得到的明文分组按照特定顺序将其重新排列，则明文数据分组更无规则可寻。
与IDEA算法中的各明文分组单独加密的方式不同的是，在X_IDEA算法中，将通过随机数发生器随机产生一个明文分组作为加密的首个明文分组，且后续加密过程中前后明文之间关系密切，算法的混淆性也进一步加强，具体详见X_IDEA的加、解密过程。
2.2 密钥生成
　X_IDEA算法中不再强调密钥为128 bit，而是通过用户输入的长度不定的初始密钥，通过密钥生成算法IDEA_KEY生成832 bit(52组×16 bit)子密钥。密钥生成算法IDEA_KEY所生成的832 bit子密钥中不能分析出弱密钥，下面介绍并分析该算法。IDEA_KEY算法如下：
　IDEA_KEY算法：
　输入：任意长度的密钥
　输出：832 bit(52组×16 bit)子密钥
Inupt KEY  //输入初始密钥
SUBKEY=””
Do While Len(SUBKEY)<=832
　L=Len(KEY)
 If GCD(L，832)=1 Then
//初始密钥的长度与832互素
        (L*T) Mod 832=1 
//计算出初始密钥长度的逆元数T
If Left(KEY，1)=”0” Then KEY=KEY/2^T Else KEY=KEY*2^T  //密钥移位
For I=1 TO L //将移位后的密钥依次赋值给子密钥
 SUBKEY=SUBKEY+Mid(KEY，I，1)
Next I
If Len(SUBKEY)=832 THEN
        Exit Do
Else
        GOTO EXT_DO
End If
Elseif L Mod 2=0 Then  
//初始密钥长度与832不互素，补位处理其长度
        KEY=KEY+”0”
        Else
        KEY=KEY+”1”
End If
EXT_DO：
Loop
　在IDEA_KEY算法中，初始密钥的长度可能≤832 bit或>832 bit。对于≤832 bit的初始密钥，每次都要经过移位后才将其逐位赋值给子密钥，而移位方向以及位数与初始密钥的首位及长度都有关系且每轮循环都在变化，密钥的首位决定移位的方向，密钥长度的逆元决定移位的位数；对于长度>832 bit的初始密钥，虽然有可能存在前832 bit相同的初始密钥，但只要其不完全相同也会生成不同的子密钥。
2.3 加密过程
　加密过程是对重组后的明文进行分组处理，每组64 bit。在所有重组好的明文分组中由随机数产生器随机产生数据X，作为加密的初始数据，X为64 bit，运用IDEA数据加密算法对数据X以及除最后一个明文分组之外的所有明文分组进行加密，产生密文C0和密文分组D1，D2，D3…Dn-1，对密文C0再次进行加密操作，将产生的密文C0′与明文P1进行“异或”操作C1=C0’⊕P1产生密文C1，再将密文D1与明文P2进行“异或”操作产生密文C2，密文D2与明文P3进行“异或”操作产生密文C3，依此方式进行运算产生直到所有的密文C=C1C2C3…Cn。最后将密文C0置于密文C头部形成总的密文C=C0C1C2…Cn。加密规则公式表示如下：
　
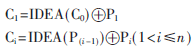
X_IDEA算法中嵌套了IDEA算法进行加密，也未对IDEA算法的加密原理及加密过程进行改变，所以X_IDEA算法的混淆性与扩散性肯定不低于IDEA算法。实际上，在X_IDEA算法的加密过程中，首个随机加密数据分组的引入以及前一密文与后一明文“异或”再产生密文的方式进一步增强了算法的混淆性。
2.4 解密过程
　解密过程是对密文进行分组处理，分为C0，C1，C2，C3，…Cn共(n+1)个组，每组也是64 bit。对密文的第一个分组C0使用IDEA数据加密算法进行加密，产生密文C0′，并将产生的密文C0′与密文C1进行“异或”操作，产生明文P1，对明文P1进行加密操作，将产生的密文与密文C2进行“异或”操作，产生明文P2，对明文P2进行加密操作，将产生的密文与C3进行“异或”操作，产生明文P3，依此方式进行运算，直到产生所有的明文P=P1P2P3…Pn。解密规则公式表示如下：

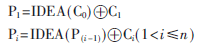
　由于加密前的明文进行过重组，所以解密完成后同样要对产生的明文进行重组工作。如果产生的明文分组后存在加密前明文重组时所补得的特殊字符，要将其去除后再进行重组。其重组过程就是加密前明文重组的逆过程。
3 X_IDEA加密性能分析
　(1)IDEA算法弱密钥问题得到有效解决
　在IDEA算法中，根据128 bit的密钥就可以得出表1，且参考文献[2]和参考文献[3]都证明了其弱密钥的存在。X_IDEA算法通过密钥生成算法IDEA_KEY生成832 bit子密钥，子密钥的生成过程无法找出固定的分析方法，因为密钥的移位及补位操作都与初始密钥KEY的长度和具体的值有关，无法进行分析。由此可见，算法IDEA_KEY产生的832 bit子密钥没有固定的位置生成表1，从而使IDEA算法的弱密钥问题得到有效地解决。
X_IDEA算法没有改变IDEA算法的加密原理，而是在用户密钥与子密钥的生成上给予了加强。用户可以随意输入密钥，通过该算法可以生成较强的子密钥；同时也可以满足对密钥强度要求较高的用户，做到密钥空间为832 bit(而不是128 bit)，因而安全性不会低于标准的 IDEA算法。
　(2)密文的明文依赖性有所提高
　在X_IDEA算法中，明文加密前先要进行重组，先后要进行两次明文分组，最后得到一个个64 bit的明文块。首个加密的明文块是通过随机数发生器确定的，并且在X_IDEA算法的加密过程中前一数据块加密后得到的密文还将数据参与后一数据块的加密。这样，加密后的密文的长度会加长。同时，如果明文发生了改变，除了会改变同部分、同组数据加密后的结果外，也会导致不同组、不同部分数据的加密结果发生改变，从而增加了数据的依赖性，使密文与明文的统计特性之间的关系更加复杂。
　(3)抗攻击能力较IDEA算法更强
　算法设计者已证明IDEA算法在加密循环过程中的第4次循环之后不再受差分密码分析的影响，因而目前也尚未出现对IDEA算法较为有效的分析方法。所以，对IDEA的攻击到目前为止仍只能采用强攻击方式。
对称密钥密码体制要求算法是公开的，其安全性依赖于密钥的安全性，密钥长度应足够长，以防止穷举式搜索方法的攻击[4]。密钥长度为1时攻击次数为21，密钥长度为2时攻击次数为22，所以算法的抗攻击能力随密钥的长度加大而增强。X_IDEA算法的密钥长度实际可达832 bit，则它的攻击次数为2832，而IDEA标准算法的攻击次数为2128次。
　(4)安全性有所提高
　由于分组密码可以作为序列密码使用，X_IDEA算法的加密过程中，加密的首个数据块以及各明文块都充当了加密密钥，根据X_IDEA算法的加密方程，在X_IDEA算法中，一次一密乱码本是由加密明文提供的，密钥是C0和P1P2P3……Pi序列的函数具有很强的随机性；而“异或”运算是非线性算法，而且在整个加密过程中相当于嵌套了IDEA算法，因而其安全性高于IDEA。
　X_IDEA算法在密钥的选择上给用户带来更大的灵活性，增强了算法的适应性，同时也消除了IDEA算法中的弱密钥，抗攻击能力进一步增强。加密前的明文重组以及初始向量的设置可以使用相同的明文加密成不同的密文，密文的明文依赖性更强。而且X_IDEA算法并没有改变IDEA算法的加密原理，只是在加密过程中嵌套了IDEA算法，所以计算量也不会增加。
参考文献
[1] 吴伟彬，黄元石.IDEA算法的改进及其应用[J].福州大学学报，2004，32(12)：28-31.
[2] 金茂顺.IDEA弱密钥[J].密码与信息，1997，61(3)：9-14.
[3] JOAN D. GOVAERTS R. VANDEWALLE J. Weak keys for IDEA. Crypto， 1993：224-231.
[4] SCHNEIER B.应用密码学[M].吴世忠译.北京：机械工业出版社，2000.