一种基于光学测角技术验证陀螺定向的方法
2009-07-10
作者:薛 瑶, 任勇峰, 崔永俊, 侯
摘 要: 介绍了由半导体激光器、线阵CCD传感器及图像采集系统等组成的小角度测量系统的工作原理,搭建了实验平台。同时,对利用数据采集系统采集陀螺仪输出的角速率进行积分,得到陀螺仪转动的角度值。通过把小角度测量系统测量的数据与积分得到的数据进行比较,验证了陀螺仪在小角度定向应用中的精确性。实验证明,该陀螺仪的测量精度达到0.01°以内。
关键词: 陀螺仪; CCD传感器; 小角度测量; 测量精度
陀螺定向技术正在被广泛应用于航空、航天、野外测绘等领域中,例如在某弹上记录系统中,使用陀螺仪对发射试验过程中试验弹的姿态进行测量。为了在实际应用中提高陀螺仪的测量精度,本文设计了一种精度高且简单易行的验证方法。
光学测角由于具有非接触性、精度高和结构简单等特点而备受人们的重视,因此使用光学测角的方法得到了越来越广泛的应用[1]。本文以微机械陀螺仪为对象,采用基于光学技术进行小角度测量的方法,设计了合理的实验方案,搭建了实验台架,对微机械陀螺仪进行了小角度定向的验证实验,并分析了实验过程中的误差来源。
1 测量方法
1.1测量装置
PA-3ARG系列三轴角速率陀螺仪是无旋转马达的固态角速率陀螺仪,用于测量三轴角速率的传感器,其分辨率达0.05°/s。如图1所示,整个测量系统由PA-3ARG角速率陀螺仪(以下简称陀螺仪)、数据采集系统、半导体激光器、平面镜、透镜、线阵CCD传感器、图像采集系统等组成。
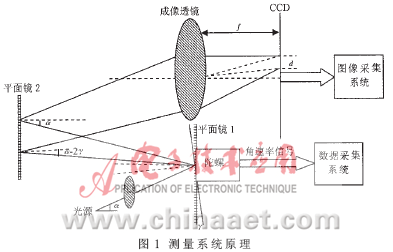
数据采集系统的主要功能是采集陀螺仪的输出信号。当陀螺仪以某个速率转动一定角度时,利用数据采集系统采集陀螺仪输出的角速率信号,对采集到的数据进行积分后即可得到陀螺仪转动的角度。为了验证该角度,本文设计了一种基于光学技术的小角度测量系统。由半导体激光器发出的连续平行激光经过聚焦透镜,入射到与陀螺仪连接在一起的平面镜1上,反射光线再入射到平面镜2上。随着陀螺仪的转动,反射光线入射在平面镜2上的位置也发生变化,经过平面镜2的二次反射后成像到位于成像透镜焦平面的CCD 靶面上。利用CCD传感器和图像采集系统可测出CCD靶面上两成像点之间的偏移距离d,根据几何关系,可求得陀螺仪的偏移角度γ与成像点的偏移距离d 之间的关系[2]。
1.2 光学测量小角度原理
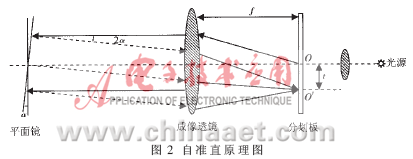
基于光学技术的小角度测量系统利用了光学自准直原理,传统的光学自准直光管原理图如图2所示[1]。光源发出的光经聚焦透镜后入射到位于成像透镜焦平面上的分划板O点处,再经成像透镜后成为平行光束;垂直于光轴安放一平面镜,则平行光束反射回来,通过成像透镜仍在分划板原来位置成实像,与原目标重合,这种现象称为“自准直”。当平面镜倾斜α角时,按光的反射定律,平行光轴的光线射向平面镜,则反射光线与原光线成2α返回,在分划板上距离O点为t的O′点处成像,t与α的关系为:

式(1)中f为成像透镜的焦距,通过测量t,即可以计算出倾角α的值。
在本测量系统中,光线在平面镜间经过2次反射,可以提高测量的灵敏度;通过光路的折叠,可以减小系统的体积。如图1所示,当陀螺仪主轴没有相对转动时,平面镜1和平面镜2相互平行,其中平面镜1为动镜,平面镜2为静止镜。入射光线经过平面镜1反射到平面镜2上,二次反射后的光线经过成像透镜后汇聚到CCD靶面上一点。当陀螺仪主轴转动一定角度γ时,平面镜1同陀螺仪主轴一同转动,两平面镜不平行,产生夹角γ,则经过平面镜1反射的光线入射到平面镜2时,入射角为α-2γ,再经过反射后,反射光线汇聚到CCD靶面上的另一点,设CCD靶面上2次成像点的距离偏移量为d,则根据透镜成像规律可得d与γ之间的关系为:
d=f tanα-f tan(α-2γ) (2)
(2)式中, f为成像透镜的焦距, α为入射光线与水平面之间的夹角,所以只需准确地测出d的值,即可得到陀螺仪转动的角度γ:
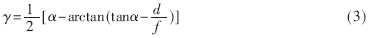
1.3 数据采集系统
数据采集系统的主要功能是采集陀螺仪输出的角速率信号。本文主要研究陀螺仪作小角度往复振动过程中的测量问题。为了便于分析数据,数据采集从陀螺仪静止开始,直到完成振动过程并回到初始状态结束。采集完成后,利用上位机对数据进行分析、处理,并进行波形显示,如图3所示,横坐标表示时间,单位为毫秒,纵坐标表示陀螺输出的角速率信号对应的电压值,单位为伏。
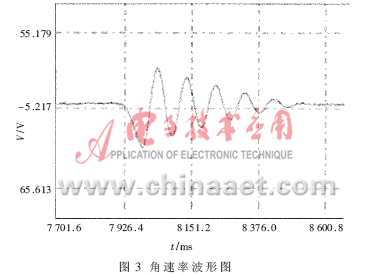
角度的计算过程:由于陀螺仪在开始时处于平衡静止状态,所以积分初始值从陀螺仪处于零位时的输出值开始,选取一定时间段的角速率信号对应的电压值后开始积分。例如,要计算图3中某点的角度值,则选取该点的前一个零位点到该点这一时间段的电压值进行积分即可。积分时需要注意:计算积分初始值时,应该取图3所示波形图中前端比较平稳的那段数据的平均值,将该值作为积分的零点,代入公式进行计算。
2 测量结果
为了验证陀螺仪的测量精度,在某次振动测量中,对采用陀螺仪测量的结果和采用光学测角方法测量的结果进行了比较,比较结果如表1所示。通过对比可以看出,陀螺仪和光学测角方法测量的结果差别在0.01°之内。

3 误差分析[2-3]
3.1 光斑的形状、CCD传感器引入的误差
理想的激光斑像点应该是单个圆滑的圆点或单根线条,但在实际测量中,点像或线像会出现许多变形,这些变形来源于光源、物体表面粗糙度和CCD传感器。当激光光束光强分布不好,物体表面粗糙或者CCD图像采集电路有干扰时,会使像点的信号强度分布出现毛刺、多峰,给探测光斑中心造成困难。另外,从CCD获得的像点数据首先要进行数字滤波,剔除随机性大的误差数据。数字滤波一般使用中值滤波方法,其依据是物体表面不会突然发生特别大的变化。当然,对于真正的物体台阶,也会有平滑作用,这样就会不可避免地引入了一定的测量误差。
3.2 零位误差
本文在原理误差的分析中假设实际测量时的起始位置与理论零位相一致,然而在实际测量中,这显然不易做到。这是因为在测量前进行光路安装调整时,一般无法使CCD图像传感器精确地位于透镜的焦平面上,而且这种不确定性带有随机性。在测量起始位置,由于CCD图像传感器不能精确地位于成像透镜的焦平面上,导致式(3)中的d值出现一定的误差。另外,对于入射光线的入射角也不能保证与理论值完全吻合,这也会引起一定的误差。因此,如何在快速高效安装调整的同时又能尽量减小零位偏移量,使零位误差影响最小,同样是高精度测量中应该重视的问题。
3.3 温度变化带来的误差
在测量过程中,假设环境空气折射率均匀分布。但是实际上温度的变化会造成空气折射率的非均匀分布,这时光线传输将发生弯曲,这将直接影响被测角度的准确性。因此,测量环境的温度分布不均匀也给测量带来了一定的误差。
本文提出了一种基于光学测角技术验证陀螺仪小角度定向的装置和方法,通过将小幅度的角度转动转换成细小的投射光点在线阵CCD靶面上较大位置的移动,以及采用2个平面镜进行二次反射,提高了系统的测量精度,减小了系统的体积。文中对基于光学技术的小角度测量结果和使用陀螺仪测量的结果进行了比较,验证了陀螺仪小角度定向的精确性,整个系统测量精度高,结构简单,具有一定的实用价值和通用性。最后,对在实际测量过程中存在的误差来源进行了分析,这对进一步提高测量精度奠定了理论基础。
参考文献
[1] 杨勇,崔秀华,徐志恒,等.一种新型用于陀螺定向的小角度测量系统的研究.航空精密制造技术,2000,36(6).
[2] 李高勇,孙志宏.线阵CCD小幅角位移实时检测系统.微计算机信息,2007,23:(6-1).
[3] 宋海峰,邓浩,张蓉,等.小角度随机往复振动条件下陀螺姿态测量研究.兵工学报,2008,29(4).

