改进的LMS算法自适应滤波器的DSP实现
2009-07-16
作者:赵巧红,曾照福
摘 要: 分析了变步长LMS算法自适应滤波器基本原理,使用MATLAB对其进行仿真,并应用SZ-EPP5402评估板进行了DSP实现,结果表明,变步长LMS算法能够克服固定步长LMS算法的矛盾,具有较快收敛速度与较小稳态误差。
关键词: LMS算法;自适应滤波器;DSP
在数字信号处理中,滤波技术占有极其重要的地位。自适应滤波器是利用前一时刻已获得的滤波器参数,自动地调节、更新现时刻的滤波器参数,以适应信号和噪声未知的统计特性,从而实现最优滤波[1]。当在未知统计特性的环境下处理观测信号时,利用自适应滤波器可以获得令人满意的效果,其性能远超过通用方法所设计的固定参数滤波器。在通信、雷达、声纳、控制工程及生物医学等领域应用广泛。
选择DSP完成自适应滤波器的设计,具有稳定性好、精确度高、不受环境影响、灵活性好等优点。固定步长LMS算法滤波器在收敛速度与稳态误差之间存在矛盾,加快收敛速度的同时也会增大稳态误差。本文使用变步长LMS算法对其进行改进,在TMS320C5402DSP芯片上实现了基于固定步长与变步长LMS算法的自适应滤波器,结果表明,变步长LMS算法自适应滤波器性能得到明显改善,在加大其收敛速度的同时也很好地减小了稳态误差。
1 自适应滤波器基本结构和LMS算法
1.1 自适应滤波器基本结构
自适应滤波器由2个分离的部分组成[2]:(1)滤波器,为完成期望的处理功能而设计;(2)自适应算法,调节滤波器系数,以改进性能。自适应横向型滤波器的结构如图1所示。图1中x(n)为输入信号,通过权系数可调的数字滤波器产生输出信号y(n),将y(n)与期望信号d(n)进行比较,得到误差信号e(n)。e(n)和x(n)通过自适应算法对滤波器参数进行调整,按照某种算法准则判断误差信号e(n)是否达到最小。重复以上过程,滤波器逐渐掌握了输入信号与噪声规律,以此为依据调节自身参数,达到最佳滤波效果。令W(n)为图1中滤波器系数矢量,即W(n)=[W0(n),W1(n),…,WN(n)],则自适应滤波器的输出为:
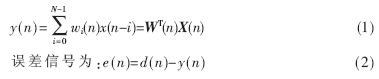

1.2 LMS算法
最常用的判断e(n)的准则为最小均方算法,即LMS算法。算法的目标是通过调整系数,使输出误差序列e(n)=d(n)-y(n)的均方值最小化,并且根据这个判据来修改权系数[3]。其中误差序列的均方值又叫“均方误差”MSE(Mean Square Error),即:

目标函数ε是W的二次函数,形成一个碗状抛物面(性能曲面),此曲面有唯一最低点即为碗底最小点,自适应滤波系数的起始值位于曲面的某一点,经过自适应调节,滤波系数变化,向碗底最小点移动,最终到达最小点[4]。系数变化按照梯度负方向移动达到最小点的速度最快,令▽(n)表示n时刻的N×1维梯度矢量,N是滤波器系数个数,自适应滤波器系数矢量的变化与梯度的关系为:
将式(7)代入式(6)得到:
初始收敛速度与稳态误差是衡量自适应滤波算法优劣的2个重要技术指标[5]。减小步长μ可减小自适应算法的稳态误差,但却减慢了算法初始收敛速度;增大步长μ可加快算法收敛速度,但却增大了稳态误差。因此,固定步长LMS算法在加快算法初始收敛速度与减小稳态误差之间存在矛盾。
2 变步长LMS算法
为了克服固定步长LMS算法收敛速度与稳态误差之间的矛盾,提出变步长LMS自适应算法。即在初始阶段选用较大步长,使算法有较快初始收敛速度,随着收敛加深之后采用较小步长来减小稳态误差。本文中变步长μ公式为:

在变步长LMS算法中,由于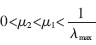 ,在此范围内,变步长LMS算法得以收敛,而由于μ(n)是变化的,在初始阶段选用较大步长μ1,使得变步长LMS算法比固定步长LMS算法具有更快的收敛速度。当算法逐渐进入收敛稳定时,选用较小步长μ2,使稳态误差随步长减小而减小,因此,变步长LMS算法具有比固定步长LMS算法更小的稳态误差。
,在此范围内,变步长LMS算法得以收敛,而由于μ(n)是变化的,在初始阶段选用较大步长μ1,使得变步长LMS算法比固定步长LMS算法具有更快的收敛速度。当算法逐渐进入收敛稳定时,选用较小步长μ2,使稳态误差随步长减小而减小,因此,变步长LMS算法具有比固定步长LMS算法更小的稳态误差。
3 自适应滤波器的MATLAB仿真
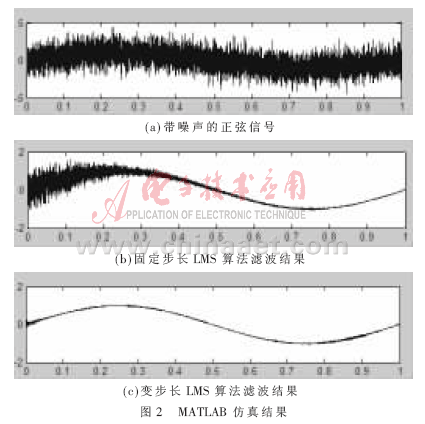
实验中,设计一个简单二阶加权自适应横向滤波器,用单频正弦信号与一个随机噪声进行叠加作为系统输入信号x(n),选取1 000个采样点,根据自适应滤波器迭代方程设计自适应滤波器,对输入信号x(n)进行滤波。固定步长LMS算法选用步长μ为0.002 6,变步长LMS算法在算法初始300个采样点时选取μ1为0.004 2,在算法初始收敛逐渐加深后,后面700个采样点选取μ2为0.002 1。仿真结果如图2所示。
从图2(b)中可以看出,固定步长LMS算法滤波结果在开始阶段收敛速度比较慢,有较大稳态误差,算法有待改善。图2(c)中变步长LMS算法滤波结果比固定步长LMS算法具有更快初始收敛速度与较小稳态误差,滤波效果得到明显改善,滤波性能优于固定步长LMS算法。从仿真角度证明了变步长LMS算法的优越性与可行性。
4 自适应滤波器的DSP实现
为了提高LMS算法的处理速度且减小系统硬件规模,采用TI公司的TMS320C5402芯片作为核心芯片实现该算法。该处理器采用程序与数据分开的哈佛体系结构,片上有16 KB存储器,外部扩展32 KB的数据存储器,64 KB的程序存储器;具有高度并行性。用C语言实现变步长LMS算法子程序流程如图3所示。其中,N为迭代次数;order为阶数;μ1、μ2为步长;count为当前采样点;NS为采样点数。
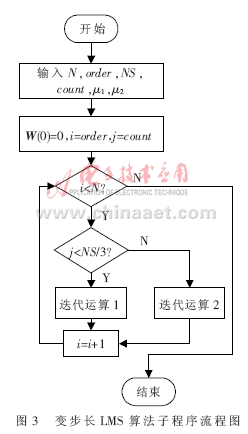
在图3中,首先输入滤波器迭代次数N,步长μ1、μ2,采样点数NS的值,初始化滤波器系数矢量W(0)为零,定义2个指针i、j,分别指向滤波器系数阶数order与当前采样点数count,当阶数小于迭代次数N,且采样点数小于总采样点数的1/3时,进行迭代运算1,此时步长为μ1;大于1/3时,进行迭代运算2,步长为μ2。
设计中,采用1 500 Hz的期望信号与312 Hz的噪声信号叠加作为30个系数的自适应滤波器的一个输入信号,对于每一个时刻n,计算自适应滤波器的输出,误差信号是输出信号与期望信号的差值。固定步长LMS算法与变步长LMS算法在SZ-EPP5402评估板上实现的结果如图4所示。

从图4(b)中可以看出,在滤波初始阶段,滤波结果不明显,输入的叠加信号经过自适应滤波器后,在初始阶段噪声没有得到明显抑制,存在较大稳态误差,收敛速度比较慢,收敛速度和稳态误差都有待改善。从图4(c)中可以看出,在滤波初始阶段,稳态误差已得到明显改善,有较小稳态误差,初始收敛速度也有所加快,输入的叠加信号经过自适应滤波器后,噪声得到明显抑制,滤波性能明显优于固定步长LMS算法,具有较快收敛速度与较小稳态误差,很好地克服了固定步长存在的矛盾。
初始收敛速度与稳态误差是衡量自适应滤波算法性能优劣的2个重要技术指标。本文通过对固定步长和变步长LMS算法自适应滤波器进行MATLAB仿真与DSP实现,比较二者结果,证明了变步长LMS算法能够保证较快的收敛速度与较小的稳态误差,并能有效去除不相关的独立噪声干扰,克服固定步长在增大初始收敛速度与减小稳态误差之间存在的矛盾,优化了自适应滤波器的性能,滤波效果明显。
参考文献
[1] SHIREEN W, TAO L I.A DSP-based active power filter for low voltage distribution systems[J].Electric Power
Systems Research,2008,78:1561-1567.
[2] 吕振肃,熊景松.一种改进的变步长LMS自适应算法[J].信号处理,2008,24(1):144-146.
[3] KUKRER O,HOCANIN A.Frequency-response-shaped LMS adaptive filter[J].Digital Signal Processing,2006,
16:855-869.
[4] 叶永生,余容桂,吴霄.一种新的自适应最小均方算法及其应用研究[J].电测与仪表,2008,45(7):19-22.
[5] 张会生,闫学斌,秦勇,等.LMS算法自适应滤波器的DSP实现[J].通信技术,2006(10):72-73.

