摘 要: 旋转、缩放和平移(RST)等几何攻击能够破坏水印检测的同步性,使得水印检测失败。针对此问题,提出了一种基于图像局部Zernike矩的RST不变零水印算法。Zernike矩的幅度具有旋转不变性,再结合图像归一化,使其具有缩放和平移不变性。由于Zernike矩的图像重构效果不理想且重构过程中复杂度高,因此水印嵌入选择零水印方案。实验结果表明,该算法对旋转、缩放和平移(RST)的攻击具有很好的鲁棒性,同时对JPEG压缩、加噪、滤波等常见的图像处理操作也具有很好的鲁棒性。
关键词: 零水印; 旋转、缩放和平移(RST); Zernike矩; 图像归一化
随着多媒体数字产品的快速发展,人们可以随意访问每个数字图像,并能对图像对象进行旋转、缩放、平移等各种几何操作。几何攻击能极大地破坏水印检测的同步性,即使微小的几何攻击也可能使水印检测失败,这使得数字图像水印技术变得更加复杂,因此,开发一种能有效抵抗旋转、缩放和平移 (RST)等几何攻击的图像水印技术迫在眉睫。
在抗几何攻击的水印方法中,不少算法利用了图像的各种不变矩,目前常用的矩主要有几何矩、中心矩和正交不变矩。Zernike矩的基是正交径向多项式,可以保证所提取的特征相关性小、冗余性小;与其他不变矩相比, Zernike矩还具有旋转不变性、对噪声的鲁棒性以及多层次表达等优点,为此,开始探索将Zernike 矩引入抗几何攻击的图像水印算法中。
针对上述问题,本文提出计算图像局部重要区域Zernike矩的抗几何攻击的水印算法。由于图像在受到旋转、缩放和平移 (RST)等几何攻击时,图像的中心不会发生变化,因此选取以图像的中心为原点,并采用图像边缘检测的方法,找到包含图像对象的局部重要区域,从而减小由于旋转带来的边缘影响,提高了Zernike矩的旋转不变性。然后,结合图像的缩放归一化,实现水印对缩放攻击的鲁棒性。由于Zernike矩的图像重构效果并不理想,而且重构过程中需要高阶矩,计算复杂度较高。因此,在水印算法的设计中,不能通过直接修改原始图像的Zernike矩并进行重构来嵌入水印,所以水印嵌入选用零水印方案。实验结果表明,该算法对旋转、缩放和平移(RST)的攻击具有很好的鲁棒性,同时对JPEG压缩、加噪、滤波等常见的图像处理操作也具有鲁棒性。
1 Zernike 矩及其性质
1.1 Zernike矩的定义
Zernike于1934年提出了一组多项式{Vnm(x,y)},这组多项式在单位圆(x2+y2≤1)内是完备正交的,其形式[1]为:


3 实验及结果
实验选取256×256的lena、128×128的camera和128×128的akiyo作为原始测试图像,为简单起见,只考虑原始图像中仅含一个图像对象且图像背景较为单一的情况。
证明该算法的可行性,256×256的lena、128×128的camera和128×128的akiyo三幅图像完全不相关,其中lena图像与camera图像的水印序列相似率sim=0.574 257<0.7,lena图像与akiyo图像的水印序列相似率sim=0.514 851<0.7,camera图像与akiyo图像的水印序列相似率sim=0.603 960<0.7。大量实验证明,不同图像由零水印构造的二值水印序列相似率都不会大于0.7。
为了测试该算法的鲁棒性,用各种几何操作对图像进行攻击实验。
3.1 旋转攻击
在数字图像处理领域中, 图像旋转有两种不同的形式[8]:Crop rotation和Loose rotation。Akiyo图像在两种不同形式下旋转30°后的水印图像如图 1(b)和图1(e)所示。

Crop rotate攻击后,本文算法水印检测响应曲线如图 1(a)所示,其中横轴表示旋转角度。可以看出,本文算法对于Crop rotate攻击,检测的相似度都在0.95以上。
Loose rotate攻击后,本文算法和参考文献[10]中的算法水印检测响应曲线分别如图 1(c)和图1(d)所示,其中横轴表示旋转角度。可以看出,本文算法对于Loose rotate攻击,检测的相似度都在0.92以上,相比于参考文献[10]中的算法,鲁棒性有一定的提高。
3.2 缩放攻击
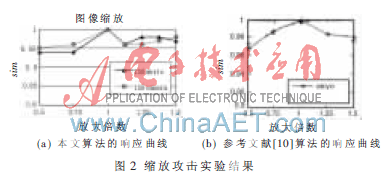
缩放攻击后,本文算法和参考文献[10]算法水印检测的响应曲线分别如图 2(a)和图2(b)所示,其中横轴表示放大倍数。对于缩放攻击,本文算法和参考文献[10]算法的鲁棒性能基本一致。
3.3 噪声攻击
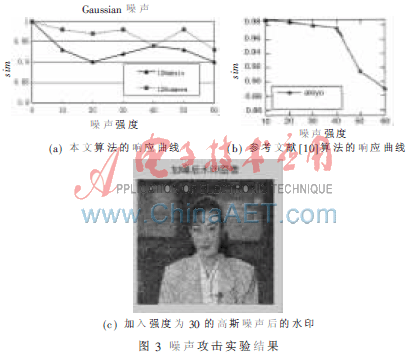
加入不同高斯噪声后,本文算法和参考文献[10]的算法水印检测响应曲线分别如图 3(a)和图3(b)所示,其中横轴表示噪声强度。Akiyo加入强度为30的高斯噪声后的水印图像如图3(c)所示。对于噪声攻击,本文算法和参考文献[10]的算法,相比鲁棒性能有一点下降。
3.4 滤波攻击
滤波攻击后,本文算法和参考文献[10]的算法水印检测响应曲线如图4(a)和图4(b)所示,其中横轴从左到右依次表示为没有受到攻击、5×5中值滤波、3×3中值滤波、3×3均值滤波、5×5均值滤波。Akiyo经过5×5均值滤波后的水印图像如图 4(c)所示。对于滤波攻击,本文算法和参考文献[10]算法的鲁棒性能几乎一样。

3.5 压缩攻击
图像经JPEG压缩攻击后,本文算法和参考文献[10]算法的水印检测响应曲线如图 5(a)和图5(b)所示,其中横轴表示压缩质量百分数。Akiyo受到压缩质量百分数为20%的JPEG压缩后的水印图像如图 5(c)所示。对于低质量压缩攻击,相比于参考文献[10]的算法,本文算法的鲁棒性有一定提高。
利用归一化后的Zernike 矩的幅度具有RST不变的性质,将从图像中提取的局部Zernike矩的幅度矢量作为图像的特征矢量,二值化后作为零水印,实现了具有RST不变性的水印。实验结果表明,该算法对旋转、缩放和平移(RST)的攻击具有很好的鲁棒性,同时对JPEG压缩、加噪、滤波等常见的图像处理操作也具有很好的鲁棒性。
参考文献
[1] KHOTANZAD A, HONG Y H. Invariant image recognition by Zernike moments[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(5):489-497.
[2] KINTNER E C. On the mathematical properties of Zernike polynomials[J].Optica Acta, 1976,23(8):679-680.
[3] 叶斌,彭嘉雄. Zernike 矩不变性分析及其改进[J].红外与激光工程, 2003(01):37-41.
[4] 马建湖,何甲兴.基于小波变换的零水印算法[J].中国图象图形学报, 2007,12(4):581-585.
[5] KHOTANZAD A, HONG Y H. Invariant image recognition by Zernike moments[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(5):489-497.
[6] XIN Y Q,LIAO S,PAWLAK M,et al. Geometrically robust image watermark via pseudo-Zernike moments[A].CCECE, 2004:0939-0942.
[7] 李雷达,郭宝龙,孙磊. 基于局部Zernike矩的RST不变水印[J]. 光电子·激光, 2007,18(1):117-120.
[8] Image processing toolbox: imroate function. http://www.mathworks.com/access/helpdesk_r13/help/toolbox/images/imrotate.html.
[9] Xiang Shijun. On invariance analysis of Zernike moments in the presence of rotation with crop and loose modes[J].Multimed Tools Appl,2010,25(5).
[10] 徐达文,王继成,王让定. 基于Zernike 矩的视频对象零水印算法[J].中国图象图形学报, 2009,14(9):1825-1831.

