基于窗函数下频谱泄露的研究
2009-07-20
作者:张 斌,孔 敏,吴从兵
摘 要: 阐述了现代信号处理的具体过程,分析了在频域中对信号进行频谱分析时产生频谱泄漏现象的原因。在分析研究传统的减小频谱泄露所采取的手段的基础上,进一步提出了如何通过合适窗函数的选择以减小频谱泄露对信号分析的影响,探讨了提高频谱分析质量的方法,并给出了相应的Matlab仿真结果。
关键词: 窗函数;频谱泄露;频谱分析
在现代信号处理中,由于信号的频域分析比时域分析具有更加清晰的物理概念和深刻含义,因而在信息技术领域FFT运算和频谱分析是一种常用的分析手段[1]。对信号进行频谱分析首先需要通过信号的傅里叶变换计算出信号对应的频谱函数。但是由于实际应用中接触到的大量非周期连续信号x(t)的频谱函数X(jω)是连续函数,利用计算机对其进行频谱分析时往往需要对信号进行离散化处理以近似分析相应的频谱。在离散化处理过程中由于被处理信号的有限记录长度和时域、频域的离散性往往造成在频谱分析中会出现一些特殊的效应:混叠现象、泄漏现象和栅栏现象。本文主要结合信号分析中常用的窗函数,针对频谱分析中出现的泄漏现象进行分析研究,给出减小频谱泄露的办法以提高频谱分析的质量。
1 泄露现象产生机理分析
利用离散傅里叶变换分析连续非周期信号x(t)的傅里叶变换X(jω),需要对于x(t)进行如图1所示的离散化处理(其中Hr(jω)为重建低通滤波器)。设x[k]表示对连续信号x[t]的等间隔T抽样得到的离散信号[2],亦即:x[k]=x(t)|t=kT,则离散信号x[k]的离散时间傅里叶变换X(ejω)与连续信号x(t)的傅里叶变换X(jω)的关系为:
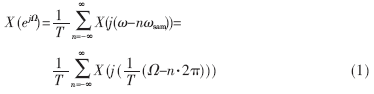

其中ωsam=2π/T=2πfsam表示对连续信号抽样的角频率,fsam为抽样频率,ω为模拟角频率,Ω为数字角频率。由(1)式可知,X(ejΩ)是X(jω)的周期化,且周期是2π。可见在满足抽样定理的前提下,采用离散手段分析连续信号的频谱X(jω)时,可以将x(t)经等间隔T抽样得到序列x[k],再对x[k]进行N点的离散傅里叶变换,得到X(ejΩ)在[0,2π)上N个频谱抽样点X[m],从而得到X(jω)的频谱信息。
如果连续信号x(t)在时域为无限长,在对其进行离散化处理后得到了离散序列x[k]也同样为无限长序列,则无法使用DFT分析,在具体的信号处理过程中往往采取对获得的离散序列x[k]进行时域加窗截短处理,使之成为有限长序列xN(k),即:

其中wN[k]为窗函数。
在信号的加窗处理过程中,常用的窗函数主要有矩形窗和汉明窗(Hamming)、汉宁窗(Hanning)、布莱克曼窗(Blackman)等非矩形窗,不同的窗函数在信号处理中对谱函数质量的影响很大[3],因此合理地选择窗函数在信号的处理中显得尤为重要。
使用长度为N的矩形窗函数RN[k]对离散序列x[k]加窗,相当于对序列x[k]直接截断,对于(2)式,采用矩形窗函数RN[k]加窗后所得序列xN[k]的频谱XN(ejΩ)为:

其幅度谱如图2所示。从图中可以看出,矩形窗的幅度谱函数主要是高度为N的主瓣以及若干个幅度较小的旁瓣组成,频谱中的旁瓣主要是由于矩形窗在两个端点突然截断而在谱中产生的高频分量引起的。因而在利用矩形窗对信号进行加窗处理时,得到的谱函数会以谱的实际频率值为中心,以窗函数频谱波形的形状向两边扩散,这样就产生了在频谱分析中所谓的“频谱泄露”现象。
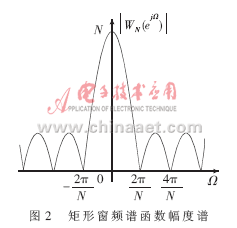
2 泄露现象的消除
泄漏现象的产生主要是由于窗函数的突然截断信号在谱函数中产生旁瓣而引起的,对于矩形窗函数的幅度谱|WN(ejΩ)|,其主瓣峰值和第一旁瓣峰值的比值为:

谱函数中主瓣的幅值与旁瓣幅度的比值越大则泄漏现象对信号频谱分析的影响就越小。增加窗信号窗口的宽度N可以增加主瓣的高度,减小其宽度,改善频谱的分辨率[4]。
设待分析连续信号为x(t)=cos(2πft),其中f=100 Hz,设采样频率fsam=600 Hz,采用矩形窗对其进行加窗截短,采样长度分别为32和64,利用Matlab软件可以得到如图3所示的仿真结果。

由仿真可以看出,增加窗信号窗口的宽度N可以减小WN(ejΩ)的主瓣宽度,改善频谱分辨率,但是减小主瓣宽度同时也降低了窗函数抑制杂波的能力;再者增加N也会增加旁瓣的能量,影响信号中弱信号频率分量的分辨,有时甚至导致更多的频率泄露,可见单纯地增加窗口宽度N并不能真正意义上地减小频率泄漏现象。
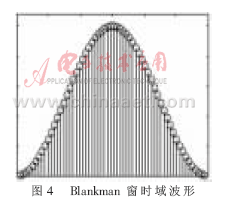
由于泄露现象是由窗函数突然截断信号x[k]而引起的,采用如图4所示幅度逐渐减小的非矩形窗对信号进行加窗[5],由于信号x[k]是被逐渐截断,在一定程度上可以减小泄露对频谱分析的影响。
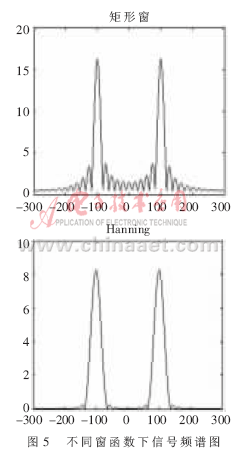
对于同样连续信号x(t)=cos(2πft),采用长度为N=32,分别用矩形窗和汉宁窗对其进行加窗截短,利用Matlab软件可以得到如图5所示的仿真结果[6]。从仿真图可以看出采用汉宁窗进行加窗截短比采用矩形窗在得到的频谱中频率的泄露要小,但是其频谱的主瓣幅值相对减小,频谱的分辨率将被降低。
当然还可以采用其他几种幅度逐渐减小的非矩形窗函数如汉明窗或者布莱克曼窗对信号进行加窗处理。对于汉明窗,其窗函数的幅度谱旁瓣的最大泄露为-41dB,大于汉宁窗的-21dB,衰减效果较为明显,但是其远隔旁瓣的衰减速度仅为-2dB/个,远远小于汉宁窗的-6dB/个,因而从整体处理效果来看,选择汉宁窗对信号进行截短处理要比采用汉明窗效果更好。对于布莱克曼窗虽然旁瓣的衰减大,但计算相对复杂,因而采用布莱克曼窗对信号进行加窗处理往往会使频谱分析趋于复杂化。
连续信号的离散化频谱分析不仅有频率泄露现象,同时还会出现诸如混叠和栅栏现象,对于混叠可以采用在抽样前添加抗混叠滤波器的方式进行处理[7],以提高频谱的分析精度。而对于栅栏现象可以在谱函数XN(ej?赘)中抽取更多的样点值,在序列xN[k]后补零构成一个L>N序列xL[k],将序列人为地改为L点,改变采样点的位置,使各采样点的间隔更小,从而提高频率检测的精度[8],减小栅栏现象对频谱分析的影响。
本文针对连续信号在频域分析中常常出现的频谱泄漏现象产生的原因进行了分析研究,提出了在频谱分析中减小频谱泄露的方法与途径,给出了Matlab软件的仿真结果。采用此种处理手段可以使信号的频谱分析精度更准确,函数谱更加贴近实际,处理效果更加理想。
参考文献
[1] 丁玉美,高西全.数字信号处理[M].西安:西安电子科技大学出版社,2000.
[2] 程佩青.数字信号处理教程第二版[M].北京:清华大学出版社,2001.
[3] 陈敏歌.基于窗函数法的FIR数字滤波器的设计[J].陕西师范大学学报,2007,35:72-74.
[4] 陈卫东,杨绍全.加窗离散傅里叶变换测频分辨率研究[J].西安电子科技大学学报,2000,27(2):157-160.
[5] 许珉,张鸿博.基于Blankman-harris窗的加窗FFT插值修正算法[J].郑州大学学报,2005,26(4):99-101.
[6] 陈怀琛,吴大正.Matlab及在电子信息课程中的应用第二版[M].北京:电子工业出版社,2003.
[7] 汪安民,王殊,陈明欣.一种抗混叠非均匀周期采样及其频谱分析方法[J].信号处理,2007,21(3):240-242.
[8] 周建雄,陈付彬.补零离散傅立叶变换的插值算法[J].信号处理,2007,23(5):690-694.

