基于分段非线性函数近似的直接数字频率合成器
2009-07-20
作者:张 鹏
摘 要: 对直接数字频率合成器(DDS)中的相位幅度转换模块提出了一种基于分段非线性函数近似的的设计方法。这种方法取代了传统的ROM查找表的方法,可以避免因采用大容量的ROM而带来的成本高、功耗大、可靠性下降等缺点。此方法对正弦函数的第一象限进行分段,在每一段内用非线性函数近似,然后再根据正弦函数的对称性质,重构完整的正弦函数。此法可以获得较好的压缩效果,并且结构简单,易于实现。
关键词: 直接数字频率合成(DDS);分段非线性函数近似;ROM容量
直接数字频率合成(DDS)是第三代频率合成技术,具有频率分辨率高、频率切换时间短、相位变化连续、易于集成等优点,被广泛地应用在通信、雷达、仪器仪表等领域。目前,在采用ROM查表方式的DDS中,为了提高频谱纯度和分辨率需要增加ROM容量(ROM容量为2W×D,W是对ROM寻址的相位位数,D是ROM的输出位数)。但大容量的ROM会使成本提高、功耗增大、速度降低且可靠性下降,因此在一定频谱纯度和分辨率的前提下研究sin存储表的压缩算法,对于降低DDS的存储容量非常有意义。本文介绍了DDS的工作原理、1/4周期压缩,提出了用分段非线性函数近似的方法代替大容量的ROM,并给出了此法在QuartusII开发环境下的原理图及时序仿真图。
1 DDS的工作原理
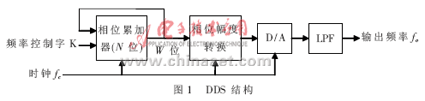
DDS的基本结构如图1所示,它由相位累加器、相位幅度转换器(常用的相位幅度转换方法是ROM查表法)、D/A和低通滤波器构成。在时钟周期的控制下,相位累加器对频率控制字K进行累加得到N位的相位累加值。N位累加值作为ROM查表的寻址地址,但在实际应用中,相位累加器输出的N位累加值,并不是全部都用来对ROM寻址,而是截取高W位对其寻址,这样可以降低对ROM容量的要求。查表输出它所对应的数字化幅度值,再经过D/A变换完成离散信号到连续信号的转变,最后经低通滤波器滤波即可得到信号输出。输出信号频率为fo=kfc/2N。
2 正弦函数1/4周期压缩
由于正弦函数sin(x)在0~2π上关于x=π奇对称,即0~π和π~2π区间相比,其对应位置的幅度值的绝对值相等,符号相反。故将π~2π区间的相位编码减去π,求出其幅度值后再加一负号,就相当于直接对π~2π区间的相位求正弦值。同时,在0~π区间,sin(x)函数关于x=π/2偶对称,故可用0~π/2区间的幅度值来表示0~π整个区间的波形。继而0~2π之间的幅度值完全可以由0~π/2区间的幅度值来实现,这样大大降低了查表的存储容量。图2表示了这种方法的实现框图。
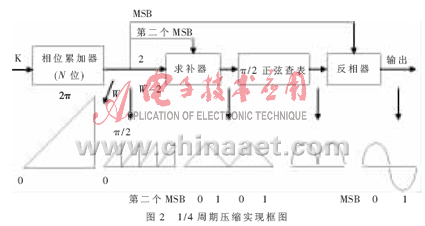
两个最高有效相位位作解码象限位,其余的W-2位用来寻址第一象限的正弦查表。最高有效位(MSB)确定结果符号,第二最高有效位确定幅度是增加还是减少。对于第一和第三象限相位,累加器的输出在第二个MSB(此时其值为0)的控制下“保持原状”,对于第二和第四象限相位,累加器的输出在第二个MSB(此时其值为1)的控制下进行二进制求补,从图形上可以看出此时锯齿波斜率在第二和第四象限是反转的。这样就形成了一个周期的正弦波[1]。
在采用1/4周期压缩的基础上,常用的相位幅度转换方法有ROM查表法、sunderland结构、sinθ-θ法、CORDIC、线性插值、泰勒近似等[3-9]。
3 分段非线性函数近似算法
3.1 算法提出
当x∈[0,1],对sin(xπ/2)进行连续等距离的M分段,在每一段内用一个二次函数近似sin(xπ/2)。a、b、c分别为二次项、一次项、常数项系数,i表示所在分段。分段数越大,近似误差就越小,但所需的ROM容量也越大,本文是在M=8的基础上展开设计的。
目前常用的非线性近似函数为泰勒二阶近似,在Matlab中对八分段的泰勒二阶近似和拟合比较,拟合方式的误差绝对值范围在1.2×10-4内,泰勒二阶级数方式的误差绝对值范围在1.8×10-4内,虽然两者相差不大,但是当对正弦函数扩大一个较大的倍数如228后,它们之间的差距就很大了,因此本文采用的是拟合方式近似正弦函数。
将x在[0,1]均匀八分段,利用Matlab中提供的拟合函数对sin(xπ/2)进行拟合,得到各段的系数如表1所示。
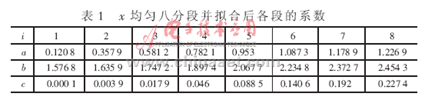
本文取W-2=14,也即对x扩大了214倍,那么对于x2就扩大228倍,为了对表达式中的三项扩大相同的倍数,将一次项系数b扩大214、常数项系数c扩大228,则此时各段系数如表2所示(其中L=214)。

由于最大幅度误差和无杂散动态范围成反向关系,为使每段的最大幅度误差下降,调整常数项系数后各段系数情况如表3所示。

这时每段的最大误差的绝对值e如表4所示。

目前常用的D/A转换器有8位、10位、12位、16位,此时的误差情况决定了最高可以采用12位D/A转换器。仔细分析后发现前三段的最大误差的绝对值较大,制约了可输出的位数。基于这样的情况,考虑将前三段再分别均分成两段,每段采用适当的非线性函数去近似正弦函数。各段系数如表5所示。

这时,每段最大误差绝对值的情况如表6所示,可以满足16位D/A转换器(其中1位是符号位,其余15位是数值位)的条件。

3.2 具体实现
相位幅度转换模块sin_r_2是根据函数表达式计算得来的,因此由乘法器、加法器和存储各项系数的模块等共同构成[2],如图3所示。
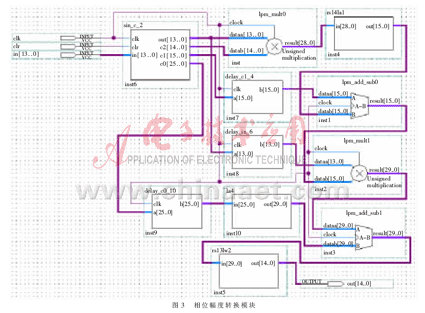
其中sin_c_2是根据输入的14位相位值的高位获得相位所在段落的二次项、一次项、常数项的系数(其中二次项系数存储的是分子,由于分母是214可以通过右移14位实现,故在此存储的是分子),二次项系数占15位,一次项系数占16位,常数项系数占26位。lpm_mult0是一个具有四级流水线的14×15乘法器,完成二次项系数中的分子与输入的相位的乘法。采用四级流水线是为了获取高的运算速度,但是运算结果是经过4个时钟周期的延迟才产生的。lpm_mult0运算结果是29位的结果,通过rs14la1模块完成右移14位,同时左补1位,结果为16位。delay_c1_4将一次项系数延迟4个时钟周期。lpm_add_sub0是一个具有二级流水线的16位减法器,它完成了-ax+b中的减法运算。delay_in_6将输入的14位相位延时6个时钟周期。lpm_mult1是个具有四级流水线的14×16乘法器,完成(-ax+b)x中的第二个乘法运算。delay_c0_10将常数项系数c0延时10个时钟周期,la4对常数项c0左补4位0。lpm_add_sub1是一个具有四级流水线的30位减法器,完成(-ax+b)x-c中第二个减法运算。rs13lw2将前一级模块的30位结果右移13位同时去掉左端的前两位。这是因为本文设计的相位幅度转换器,可以满足后接16位D/A转换器的要求(其中第一位是符号位,后面15位是数值位)。30位的计算结果前两位始终为0,可以将此去掉,再去掉计算结果中的后13位,剩下的15位送往D/A转换器。这样就完成了相位幅度转换。
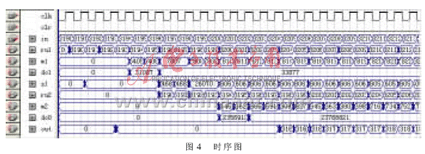
时序图如图4所示,信号in对应sin_c_2中输入的14位相位,ru1对应sin_r_2输出的14位相位值out[13:0],m1是lpm_mult0输出的结果,dc1是delay_c1_4的输出结果,s1是lpm_add_sub0的输出结果,ru2是delay_in_6输出结果,m2是lpm_mult1的输出结果,dc0是delay_c0_10的输出结果,out是rs13lw2的输出结果。从时序图中可以看出,经过14个时钟周期的延迟,最后输出正确的结果。
3.3 比较
本文设计的相位幅度转换器主要特点是ROM容量的压缩。首先在Matlab中仿真得知,在八分段中采用拟合方式近似比采用泰勒二阶近似误差范围小,所以采用的是拟合方式的函数近似。其次,通过分析可知八分段的方法中最高可以满足14位D/A变换的要求,需存储8×(15+16+26)=456 bit的信息,若采用常规的ROM查表法在相同条件下(W-2=14,D=11)所需ROM容量为214×11=180 224 bit。再次,为了进一步改善输出频率的频谱特性本文将误差较大的前三段每段再次均分为两段,这时就可以满足16位D/A变换的要求,需存储11×(15+16+26)=627 bit的信息,若采用常规的ROM查表法在相同条件下(W-2=16,D=15)所需ROM容量为214×15=245 760 bit。可见这种方法只需进一步划分不符合要求段落的分段就可以获得更好的频谱特性,因此具有很强的灵活性。
本文通过仿真比较,提出了一种针对八分段、十一分段的分段非线性函数近似的方法去实现DDS中的相位幅度转换器。与过去常规的ROM查表法相比较,它可以获得较好的压缩效果。在QuartusII开发环境下搭建了利用此方法所实现的相位幅度转换器的结构图,并得到了它的时序仿真图。通过验证,本法可以很好地实现相位幅度转换的功能。在具体的实现中采用(-ax+b)x-c形式,比用-ax2+bx-c形式节省了一个乘法器,充分利用数字电路中的右移特性实现除法运算,总共用了两个乘法器和两个减法器,结构简单、灵活,易于实现。
参考文献
[1] 白居宪.直接数字频率合成[M].西安:西安交通大学出版社,2007.
[2] 刘波.精通Verilog HDL语言编程[M].北京:电子工业出版社,2007.
[3] 徐海燕,田增山.直接数字频率合成中的相位杂散抑制方法研究[J].电信交换,2007(4):15-18.
[4] 何方勇,陈建安.基于线性插值的DDFS中的相位-幅度映射研究[J].现代雷达,2006,28(1).
[5] 王春林,吴建辉,叶双应,等.一种基于非均匀分段线性插值的直接数字频率合成器[J].电子器件,2006,29(2).
[6] 木霄易,刘丽蓓,邵丙铣.一种高性能低功耗直接数字频率合成器的设计[J].微电子学与计算机,2007,24(1).
[7] LANGLOIS J P M, Al-KHALILI D.Piecewise continuous Linear interpolation of the sine function for Direct Digital Frequency Synthesis[J]. Radio Frequency Inteqrated Circuits(RFIC) Symposium, 2003 IEEE 8-10 June 2003.
[8] LANGLOIS J P M, Al-KHALILI D. A new approach to the Design of Low Power Direct Frequency Synthesizers[C]. IEEE International Frequency Control Symposium and PDA Exhibition 2002.
[9] VANKKA J. Methods of mapping from phase to sine amplitude in direct digital synthesis[J]. IEEE International Frequency Control Symposium, 1996.

