文献标识码: A
文章编号: 0258-7998(2011)10-0087-04
目前已经建成和正在建设中的现代GNSS系统都是采用直接序列扩频(DSSS)通信体制,其本身具有一定的抗干扰能力[1]。但由于GNSS卫星信号发射功率有限,传输距离遥远,在地面接收到的导航信号功率十分微弱,极易受到来自地面或近地空间的电磁干扰,特别是在军事应用中,还可能受到敌方的有意干扰。无论是有意干扰还是无意干扰,只要干扰信号强度超出系统自身抗干扰容限,GNSS接收机的定位服务质量就急剧恶化。在各种干扰形式中,窄带干扰最为常见且危害很大。因此研究GNSS接收机的窄带干扰抑制技术对高性能接收机的开发和卫星导航的应用具有十分重要的意义。
常用的窄带干扰抑制方法可分为时域处理和频域处理两类。时域处理方法主要是基于线性或非线性的预测滤波技术[2-3],当干扰快速变化时,这种技术就不再适用。频域处理方法主要是利用了在变换域映射后,扩频信号和背景噪声的频谱十分平坦,而窄带干扰的频谱呈脉冲状,集中在某些频点上,可以进行快速干扰识别及滤除。但在实际应用中,如果对信号直接分块进行DFT运算,会产生严重的频谱泄露[4],它使干扰能量在频域中扩散,影响后续的干扰抑制处理。为了减轻频谱泄露问题,大多数频域干扰抑制技术都是对分块数据先进行时域加窗再进行DFT变换。窗函数的引入,扭曲了数据块边缘处的有用信号,带来了信噪比损失的问题,且使得处理后恢复出的信号失真较大。为此,MITRE公司的CAPOZZA等人提出50%重叠加窗DFT处理算法[5]改善了信噪比插入损耗问题。后来JONES等人提出用临界采样DFT滤波器组进行频域处理抑制窄带干扰[6]。参考文献[7]对上述两种算法进行了详细的比较,认为在采样相同DFT长度的情况下,50%重叠加窗DFT算法具有更小的插入损耗,临界采样DFT滤波器组算法则具有更小的频谱泄露。为了兼顾频谱泄露抑制能力与插入损耗,本文提出了基于过采样DFT滤波器组的窄带干扰抑制方法。与CAPOZZA的加窗DFT处理方法相比,DFT滤波器组具有频谱泄露小的优点,具备更强的干扰抑制能力;而与JONES的临界采样DFT滤波器组相比,过采样DFT滤波器组能够在减轻频谱泄露的同时,实现信号的近似完全重构(NPR),插入损耗更小。
1 DFT滤波器组
滤波器组的基本思想是将输入的全带信号,经过一组分析滤波器分解成若干个子带信号,然后针对各子带信号的特点分别进行处理,最后再通过一组综合滤波器重构出原信号[8]。合理地分析/综合滤波器组的设计,可以使得信号完全准确重构。图1为M通道临界采样滤波器组结构图。
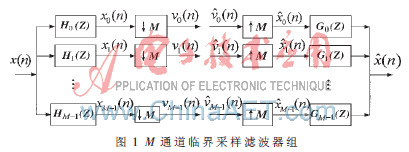
分析滤波器组主要负责频谱分解。有一种分析滤波器hm(n)设计思路是由一个原型低通滤波器h(n),经过线性调制,在频谱上依次移位衍生而成。即:
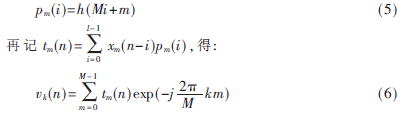
这即为M点的DFT形式,类似的分析也可将组合滤波器组变换成逆DFT的形式。于是,得到M通道临界采样DFT分析滤波器组的多相结构如图2所示,其中降采样率K=M。

图2中各通道中的多相滤波器pk(n)长度为I,由原型低通滤波器h(n)经M倍抽取而得到。一种可行的近似完全重构的滤波器组设计方法是,分析/综合滤波器组基于同一个原型低通滤波器衍生而来,利用窗函数法设计出此原型低通滤波器[9],方法如下: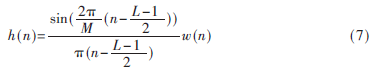
其中w(n)为某长度为L的窗函数。综合滤波器组原型滤波器设计为g(n)=h(-n)。图2中的临界采样滤波器组,在子带混叠小与信号完全重构上难以同时兼顾。如果图2中的降采样率K<M,则为过采样滤波器组,过采样滤波器组能够在子带混叠很小的同时,实现信号的近似完全重构,其设计有很多方法[9-10]。
2 基于DFT滤波器组的干扰抑制方法
2.1 基于DFT滤波器组的干扰抑制模型
接收到的GNSS基带信号经过DFT分析滤波器组之后,各子带的输出即为其频谱输出,在频域进行干扰检测时,对存在干扰的谱线进行适当处理,达到抑制窄带干扰的目的,然后经过综合滤波器组,重构出滤除掉干扰后的原GNSS信号。基于DFT滤波器组的窄带干扰抑制模型如图3所示。
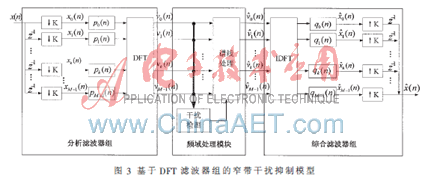
2.2 频域干扰抑制处理算法
在接收到的导航信号中,有用信号淹没在背景噪声下,因此在带内没有干扰的情况下,主要是高斯噪声在该频带内的频率分量。由于DFT对信号进行的是线性变换,所以DFT后的带内每一个频率分量仍是高斯分布的。设原时域高斯噪声均值为0,方差为σn2,则可算得M点DFT得到的各频率分量满足均值为0,方差为Mσn2的高斯分布,其幅度值满足Rayleigh分布,此Rayleigh分布概率密度函数与概率分布函数分别为:
其中,vk(n)为DFT分析滤波器组输出的各谱线复数值,Th(n)表示估算的第n帧的背景噪声门限,Ak(n)为此帧中所有低于当前门限的谱线幅度,Sk(n)对这部分谱线进行计数。当阈值估计趋向稳定时,便得到背景噪声包络,即为门限。对幅度值超过门限的谱线,认为是干扰信号,直接置零滤除干扰。
3 性能分析与仿真比较
3.1 性能分析与对比
当临界采样DFT分析滤波器组的原型低通滤波器长度L=M且h(n)=w(n)时,此分析滤波器组就退化为加窗后的DFT;如果L=M,且h(n)≡1,则此分析滤波器组就进一步退化为单纯的DFT。其实单纯的DFT变换本身就可以看作是幅频响应为|sin(ωM/2)/sin(ω/2)|的低通滤波器衍生出的一个均匀窄带滤波器组[8],由于sinc函数旁瓣电平高,且只在圆频率为2π/M的整数倍处为0,所以滤波器组内各子带之间存在较多混叠,这也就是直接进行DFT会造成较多的频谱泄漏的原因。当干扰信号的圆频率不是2π/M的整数倍时,各子带滤波器在此处旁瓣电平都不为0,则干扰频率就会泄漏到所有的子带上。
加窗时的泄漏分布取决于所采用窗函数的频域特性,不加窗相当于使用矩形窗。矩形窗主瓣宽带窄但旁瓣电平高(最大-13.56 dB),干扰信号很强时,其泄露出的旁瓣会在很宽的频带范围内都高于背景噪声。而对于非矩形窗,由于其旁瓣电平低,减轻了干扰信号的频谱泄露。以Blackman-Harris(4-term)窗为例,其主瓣宽度为12π/M[4],即无论DFT长度M为多少,其主瓣都会占用约7个频点,而其最大旁瓣电平却低至-57 dB,当应对强于背景噪声50 dB的单音干扰时,Blackman-Harris (4-term)窗处理后的频谱中仅有约7个频点的电平高于背景噪声。但是窗函数的使用会带来相当的信噪比损失,损失程度可表示为式(16)[12]。仍以256点的此窗为例,信噪比损失达3.04 dB。
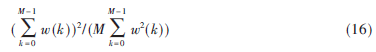
而对第二节中分析的DFT滤波器组方法而言,可以将其分析滤波器组看作是一个用L长的时间窗函数截取信号后做M点DFT,例如L=3M时,式(6)等效于在做了L点DFT之后,再在频域进行3:1抽取,显然这比传统加窗DFT的频谱泄露的点数会更少。而过采样滤波器组能在临界采样滤波器组基础上更进一步,既满足频谱泄露少,又能信号近似完全重构,使得信噪比处理损耗很小。
3.2 仿真结果对比
下面以2.046 MHz带宽的GPS C/A码信号进行比较实验,设定输入信噪比为-20 dB,再加入两个干信比都为70 dB的单音干扰,分别采用未加窗DFT、加窗DFT、DFT滤波器组三种方法进行窄带干扰抑制实验。加窗DFT的窗函数采用参考文献[5]推荐的Blackman-Harris窗; 滤波器组的原型滤波器长度L=3 M,所用窗函数与上述相同。
图4中实线为采用相同的频域自适应估计算法分别得到的干扰门限。所加入的两个单音干扰,第一个的圆频率恰好为2π/M整数倍,后一个不是;而在现实场景中由于信号多普勒频移的不确定性以及干扰的不可知性,窄带干扰一般都不在2π/M整数倍频点上。
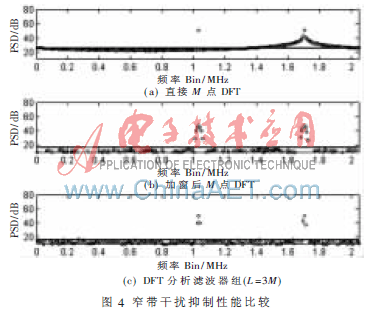
通过图4可以看到,直接DFT得到的频谱在第二个干扰源附近有很严重的频谱泄露,如果采用频域滤除的方法会滤除掉相当大一部分有用信号,所以这种方法极不实用。若采用加窗后的DFT,每个强单音干扰要滤除约7个频点。而采用(过采样或者临界采样)DFT滤波器组方法,每个强干扰只需滤除约3个频点。一般认为,低于25%的GNSS信号带宽被滤除后的信号导航性能都仍然能够接受[7]。因此,如果采用M=256点的DFT,则加窗DFT方法能够承受约25%×256/7≈9个这样的单音干扰,而DFT滤波器组方法能够承受约25%×256/3≈21个这样的单音干扰。由此可知,在相同DFT长度情况下,过采样和临界采样的DFT滤波器组,都比加窗DFT有更强的干扰抑制能力。
下面比较过采样和临界采样两种DFT滤波器组的处理方法,以及50%重叠加窗对信噪比的影响。把不含干扰的GNSS信号分别经历这三种不同处理流程,三种方法的DFT长度都为M,其中过采样DFT滤波器组的降/升采样率K取M/2,M=256。对通过几种常用窗函数设计出的滤波器组,分别进行对比仿真实验,得到如表2所示的插入损耗结果。可见,在采用相同窗函数设计出的原型滤波器的情况下,过采样DFT滤波器组的插入损耗比临界采样DFT滤波器组明显要小,但略高于50%重叠加窗方法。

通过仿真实验与对比分析表明,这种方法在抑制频谱泄露方面的能力,与临界采样滤波器组相同,都优于CAPOZZA提出的重叠加窗DFT处理方法[5];而在插入损耗方面,与重叠加窗DFT相当,都优于JONES等人提出的基于临界采样滤波器组的处理方法[6]。
综上所述,基于过采样DFT滤波器组的窄带干扰抑制方法兼具了上述二者的优点,兼具优越的频谱泄露抑制性能和微小的插入损耗,在GNSS抗干扰领域具有广泛的应用前景。
参考文献
[1] KAPLAN.GPS原理与应用[M].寇艳红,译北京:电子工业出版社,2007:181-208.
[2] POOR H V, RUSCH L A. Narrowband interference supp ression in spread spectrum CDMA [J]. IEEE Pres. Third Quarter, 1994(8):14-27.
[3] VIJAYAN R, POOR H V. Nonlinear techniques for interference suppression in spread spectrum systems. IEEE Trans. Commun., 1990,38(7):1060-1065.
[4] 应启珩.离散时间信号分析和处理[M].北京:清华大学出版社,2001:103-105, 228-234.
[5] CAPOZZA P T, HOLLAND B J. A single-chip narrowband frequency domain excisor for a global positioning system(GPS) receiver. Custom Integrated Circuits Conference, May 16-19, San Diego, California.
[6] JONES W W, JONES K R.Narrowband interference supppression using filter-bank analysis/synthesis techniques[C]. IEEE MILCOM Conference, San Diego, California, Paper 1992,38(1):1.
[7] RIFKIN R, VACCARO J J. Comparison of narrowband adaptive filter technologies for GPS[R]. Position Location and Navigation Symposium, IEEE, March 2000.
[8] 胡广书.现代信号处理教程[M].北京:清华大学出版社,2004:219-225.
[9] YIU K FC, GRBIC N, NORDHOLM S. Multicriteria design of oversampled uniform DFT filter banks[J]. Signal Processing,IEEE, 2004,11(6):541-544.
[10] TANAKA T.A direct design of oversampled perfect reconstruction FIR filter banks. Signal Processing,IEEE,2006,54(8):3011-3022.
[11] 梁继业, 刘会杰.卫星扩频通信中一种简化的窄带干扰抑制方法[J]. 电路与系统学报, 2004,9(6):86-89.
[12] HARRIS F. On the use of windows for harmonic analysis with the discrete Fourier transform.Proc.IEEE,1978, 66:51-83.

