一种新的求解0-1背包问题的自适应算法
2009-08-11
作者:龚文引,蔡之华,詹 炜
摘 要: 提出了一种新的求解0-1背包问题的自适应算法——改进郭涛算法IGT。新算法实现了真正意义上的子空间搜索过程,引入了变维子空间,加入了变异算子,同时还与贪心算法相结合,并引入启发式修正算子,以保证算法的局部搜索能力和群体多样性。
关键词: 0-1背包问题 改进郭涛算法 贪心算法 局部搜索 启发式修正算子
0-1背包问题是一类经典的组合优化问题,它已被证明是一类NP完全问题。因此,用通常的数学方法求解很难在有效的时间内找出全局最优解。对0-1背包问题的研究具有现实意义,它可以广泛运用于资源分配、投资决策、货物装载等方面。例如:处理机和数据库在分布式计算机系统上的分配问题;项目选择的货物装载问题;削减库存问题等。目前,对此类问题的研究已出现了不少有价值的方法。这些方法主要分两大类:一类是精确方法,如:分支-定界法、动态规划法、隐枚举法等;另一类是启发式方法,如:贪心算法、遗传算法、模拟退火算法、Tabu搜索算法等。
由于0-1背包问题的复杂性,因此,在求解此类问题时容易陷入局部最优解。为此,本文对基本的郭涛算法进行了一些改进,并结合贪心算法对这一类问题进行了研究。通过大量的数据模拟实验,证明了新算法在求解0-1背包问题时具有很好的有效性和稳定性。同时,由于算法采用了“群体爬山策略”,所以很容易找出全局最优解。
1 0-1背包问题
0-1背包问题可以形式化地描述为:

其中:式(1)为目标函数,式(2)和(3)为约束条件,X为一个n维的向量,ci表示第i个物品的价值,wi表示第i个物品的重量,n为物品的数量。如果第i个物品放入背包中,则xi=1,否则xi=0。问题的目标就是要在背包尽量装满但又不超过其容量的情况下,使所装入背包中的物体价值最大。此问题的复杂度为O(2n)。
2 郭涛算法简介
郭涛算法[4]是由郭涛等提出的一种启发式演化算法,主要是为了解决带不等式约束的函数优化问题。实践证明,郭涛算法在求解带等式或(和)不等式约束的函数优化问题中取得了很好的效果。本文把郭涛算法加以改进后应用到0-1背包问题求解中,取得了很好的效果。
郭涛算法的特点为:
(1)采用了演化算法中的群体搜索策略,保证了搜索空间的全局性,有利于搜索问题的最优解。
(2)采用了随机子空间的随机搜索,并采用多父体杂交和非凸子空间搜索策略,保证了随机搜索的遍历性。
(3)采用了“劣汰策略”,每次只淘汰群体中最坏的个体,淘汰压力小,从而保证了群体的多样性。同时,这样的策略也可以保证上一个群体的最好个体始终完好无缺地在下一个群体中出现。而这样做就可以保证算法以概率1收敛到全局最优解[3]。
(4)算法采用的是群体爬山策略,保证了整个群体最后集体登上最高峰(深谷)。当最优解不惟一时,该算法还可能一次同时找到多个最优解[6]。
3 改进郭涛算法及问题处理
3.1 编 码
由于郭涛算法很适合用实数编码,因此,本文在求解0-1背包问题时也采用了实数编码。具体作法是:首先使xi在[0,1.999999]之间随机取值,在进行多父体杂交形成新的个体时就利用这些实数数据进行计算;其次,在求解函数适应度的时候,利用函数yi=INT(xi)把xi整型化,从而使yi取值为0或1,即表示物品是否装入背包中。
3.2 适应度函数设计
由于0-1背包问题有约束条件的限制,因此,在计算个体适应度值时,该个体必须满足约束条件。为此,本文把适应度函数分为目标适应度函数和约束适应度函数两类。
约束适应度函数为:

3.3 比较函数Better(X1,X2)的处理
由于要比较两个个体的优劣,因此,在郭涛算法中设计了一个布尔型比较函数Better(X1,X2),通过这个函数来比较两个个体的优劣。由于问题求解的需要,本文对这个函数作了一些修改,具体如下:
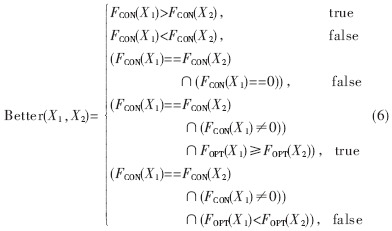
3.4 对基本郭涛算法的几点改进
(1)子空间搜索策略。原算法在张成的子空间V中只是通过杂交选出一个个体。本文采用文献[6]中的方法:先从子空间V中选出S个个体,然后在这S个个体中找出一个最好的个体X′。这样做就实现了真正意义的子空间搜索策略。
(2)变维子空间策略。当群体接近最优解时,可以缩小搜索空间,即减小子空间的维数。
(3)引入变异算子。这是因为变异算子可以增强算法的局部搜索能力,同时,还可以保证群体的多样性,防止早熟。
(4)与贪心算法结合,引入启发式修正算子。为了更进一步地增强算法的局部搜索能力(因为郭涛算法的全局搜索能力很强),本文把基本郭涛算法与贪心算法相结合,使用启发式修正算子,用它来保证解的可行性,使得搜索总能在可行解的空间上进行,并在保证解可行性的前提下,尽量增加适应度值。具体做法是从每次执行完杂交和变异后形成的新群体中随机地选择不包括最好个体在内的T个个体,然后对这些个体作一定的修正。该算子分为删除和增加两个阶段。首先是删除阶段,按ci/wi由小到大的方向把xi由1变为0,直到把不合法的解变成合法的解,若个体原本是合法个体,则不进行删除操作;接着是增加阶段,在保证解的可行性前提下,按ci/wi从大到小的方向把xi由0变为1,尽量增加适应度值,这就使个体得到了改良。
3.5 改进的郭涛算法
改进郭涛算法可以描述为:

改进的郭涛算法除继承了基本郭涛算法的优点之外,还具有如下特点:(1)实现了真正的子空间搜索策略;(2)变维子空间的引入使算法收敛更快;(3)加入了变异操作和使用启发式修正算子,从而增强了算法的局部搜索能力;(4)修正算子对新产生的群体中的部分个体进行了修正,不仅可以保证搜索总能在可行解的空间上进行,而且还可以使群体保持多样性。
4 数值实验
为了能够验证改进郭涛算法的有效性和稳定性,本文首先通过数据实验对基本郭涛算法和改进郭涛算法进行对比,然后,在改进郭涛算法的基础上,采用了两种方式来进行模拟实验。一种方式的数据来源于目前国内比较常见的遗传算法书籍中关于0-1背包问题的示例;另一种方式的数据则是通过随机产生的十组数据,每组数据wi的取值范围是[0,999],各组中数据的个数分别是20,20,50,50,60,60,80,80,100,100个。这样可以通过比较来测试算法的收敛性、稳定性以及有效性。
实验环境:CPU——P-IV 1.7GB;内存——256MB;操作系统——Windows 2000 Server;开发程序——VC++ .net 2003。
4.1 测试1:基本郭涛算法与改进郭涛算法的对比
参数设置:群体规模N=50;初始子空间大小M=8;变异概率p_mutation=0.001;通过杂交新产生个体数目S=8;修正个体数目T=5,每次实验运行100次。实验Data1、Data2的数据来源于文献[12],最大演化代数MaxGen=2000;实验Data3的数据来源于文献[13],最大演化代数MaxGen=10 000;实验Data4的数据来源于文献[14],最大演化代数MaxGen=10000。基本郭涛算法与改进郭涛算法实验结果比较见表1。
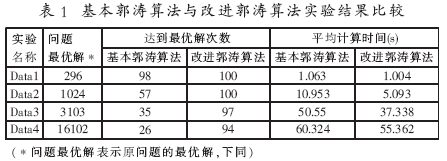
从表1的比较结果中可以看出:改进的郭涛算法比基本郭涛算法表现出更好的性能,特别是在物品的数目很大时,它的优越性(如:达到最优解的次数和计算时间)得到了更好的体现。
4.2 测试2:数据来源于常见的遗传算法文献
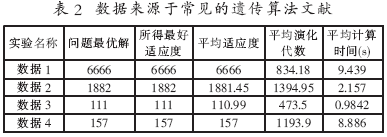
参数设置:群体规模N=50;初始子空间大小M=8;最大演化代数MaxGen=2000;变异概率p_mutation=0.001;通过杂交新产生个体数目S=8;修正个体数目T=5,每次实验运行100次。计算结果见表2。其中数据1、数据2来源于文献[11],数据3、数据4来源于文献[1]。
4.3 测试3:通过随机产生10组数据的结果
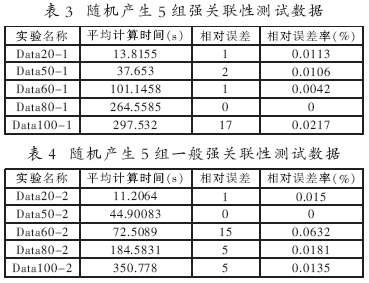
参数设置:群体规模N=100;初始子空间大小M=8;最大演化代数MaxGen=10000;变异概率p_mutation=0.005;通过杂交新产生个体数目S=8;修正个体数目T=10,每次实验运行50次。表3为随机产生的5组强关联性(Strongly correlated instances)数据的计算结果;表4为随机产生的5组一般强关联性(Almost strongly correlated instances)数据的计算结果。注:相对误差率=(最好适应度-最坏适应度)/平均适应度×100%;相对误差=最好适应度-最坏适应度。
4.4 结果分析
表2中的数据由于物品的数量相对比较少,因此,在利用本文中的算法进行计算时稳定性很好,而且收敛得也比较快,基本上都能求出问题的最优解。从表3和表4中数据的计算结果可以看出,随着物品数量的不断增加,计算时间基本上在不断增大,但是由于问题的复杂性是成指数性增长的,而本文中的计算时间并没有快速增加,所以这种时间的增加是可以接受的。并且,计算结果的相对误差率都在10-4左右。通过对两个表中的数据进行分析可以看出,新算法具有很好的稳定性和有效性。
5 结 论
本文为了求解0-1背包问题,在基本郭涛算法的基础上对其作了一些修改,形成了改进的郭涛算法(IGT)。通过大量的数值模拟实验证明了改进郭涛算法在求解0-1背包问题时是很有效的,而且具有很好的稳定性。当然,在随着物品的数目不断增加时,新算法收敛的还不是很快,这将在今后的工作中做进一步的研究。
参考文献
1 康立山,谢云,尤矢勇等.非数值并行算法(第一册)——模拟退火算法.北京:科学出版社,1995
2 王小平,曹立明.遗传算法——理论、应用与软件实现.西安:西安交通大学出版社,2004
3 胡欣,汪红星,康立山.求解多维0-1背包问题的混合遗传算法.计算机工程与应用,1999;(11)
4 郭涛,康立山,李艳.一种求解不等式约束下函数优化问题的新算法.武汉大学学报(自然科学版),1999;5(45)
5 李艳,康卓,刘溥.郭涛算法及其应用.武汉汽车工业大学学报,2000;3(22)
6 康卓,李艳,刘溥等.一种通用的混合非线性规划问题的演化算法.计算机研究与发展,2002;11(39)
7 GAO HP,XIAO XH,YANG ZQ et al.A mixed evolutionary algorithm consisting of global and local search to solve multi-modal function optimization ptoblem.Journal of Huanggang Normal University,2003;6(23)
8 潘正君,康立山,陈毓屏.演化计算.北京:清华大学出版社,广西科学技术出版社,2000
9 Freville A,Plateau G.Hard 0-1 test problems for size reduction methods.Investigation Operativa,1990;(1)
10 Hanafi S,Freville A.An efficient tabu search approach for the 0-1 multidimensional knapsack problem.European Journal of Operational Research,1997
11 陈国良,王煦法,庄镇泉等.遗传算法及其应用.北京:人民邮电出版社,2001
12 马良,王龙德.背包问题的蚂蚁优化算法.计算机应用,2001;21(8)
13 张铃,张钹.佳点集遗传算法.计算机学报,2001;24(9)
14 金慧敏,马良.遗传退火进化算法在背包问题中的应用.上海理工大学报,2004;26(6)

