摘 要: 针对资源受限项目调度问题,提出了一种基于人工蜂群算法的优化方法。人工蜂群算法中每个食物源的位置代表一种项目任务的优先权序列,每个食物源的位置通过扩展串行调度机制转换成可行的调度方案,迭代中由三种人工蜂执行不同的操作来实现全局最优解的更新。实验结果表明,人工蜂群算法是求解资源受限项目调度问题的有效方法,同时扩展调度机制的引入可以加速迭代收敛的进程。
关键词: 资源受限项目调度;人工蜂群算法;扩展串行调度
现代项目管理的理念和方法已经被越来越多的组织所接受,成为组织模式中不可或缺的一部分,而项目调度是项目管理中最具挑战行性的工作。由于项目的可用资源稀缺及项目任务间的必须满足的工序关系,使得项目调度成为一个十分复杂的问题。资源受限的项目调度RCPSP(Resource-Constrained Project Scheduling)问题是一类典型的组合优化问题,在理论上Blazewicz[1]已经证明它属于强NP-hard问题,对于大规模的项目调度采用精确解法求解就变得十分困难,而启发式算法在求解速度上则表现出明显的优越性。近年来国内外学者对基于优先规则的启发式算法做了大量的研究,先进进化和智能算法不断出现(如模拟退火算法、禁忌搜索算法、遗传算法,及蚁群算法、粒子群算法等),并被逐步应用到RCPSP问题求解中。
受到蜜蜂群体采蜜行为的启发,2005年Karaboga[2]提出了一种基于蜂群智能的新的人工蜂群算法ABC(Artificial Bee Colony)。Karaboga等[3-4]已经验证与遗传算法、差分进化算法及粒子群算法相比,ABC算法在连续型多峰函数寻优问题中能得到更好的结果。ABC算法是连续性问题优化提出的,在离散性问题,如组合优化等问题中的应用还比较少。
本文根据资源受限项目调度问题的解的特点,提出了一种基于优先权的求解RCPSP的人工蜂群算法,并通过实例仿真验证了算法的有效性。
1 问题描述
典型的资源受限项目调度问题基于下述假设:(1)组成项目的各任务是确定的,且工期已知;(2)每项任务必须在其所有的紧前任务完成后方能开始;(3)项目的可用资源为多种可更新资源,已知资源可用量的最大限额且在项目整个过程中保持不变;(4)任务不可拆分,即任务一旦开始不得中断;(5)调度的优化目标是项目工期最短。因此,RCPSP可描述为:设项目的任务集为J={0,1,2,…,n,n+1},其中任务0和n+1为虚任务,工期为0,分别代表开始任务和结束任务。sj=fj-dj,C={(i,j)|i必须在j开始前完成}为项目的紧前任务集,其中sj、fj、dj分别表示第j项任务的开始时间、结束时间和总耗时。设项目共有K种可更新资源,第k种资源的总量为Rk,第j项任务对第k种资源的需求量为rjk。则资源受限的项目调度的数学模型为:

2 人工蜂群算法求解RCPSP
2.1 人工蜂群算法简介
人工蜂群算法是一种基于群智能的元启发算法,因其原理简单易于实现的特点受到了越来越多的关注。人工蜂群算法中有两个重要组成:人工蜜蜂和食物源。人工蜜蜂分为三类:工作蜂、跟随蜂和侦查蜂,每一种人工蜂扮演不同的角色。工作蜂在蜜源采蜜,并将蜜源信息带回与跟随蜂分享;跟随蜂等候在蜂巢从回来的工作蜂那里得到食物源的信息;侦查蜂负责寻找新蜜源。工作蜂通过在蜂巢跳舞场以“摆尾舞”的方式分享信息,其舞蹈形态和采蜜蜜源的蜂蜜量成正比。跟随蜂观察舞蹈,然后依据分享蜜源的蜂蜜量选择适当的食物源,好蜜源将会吸引更多的跟随蜂。当一个蜜源被多次采蜜后,就会被抛弃,然后侦查蜂就会勘探另一个新蜜源。因此,侦查蜂的作用可以看做是开发食物源,而工作蜂和跟随蜂的作用是开采食物源。蜂群按数量等分成两组,前一半是工作蜂,后一半是跟随蜂。每一个工作蜂对应一个食物源,即工作蜂的数目和蜂巢周围的食物源的数目相等。在ABC算法中食物源即蜜源,每个食物源的位置代表优化问题的一个可行解,食物源的蜂蜜量称为适应值,代表相关解的质量。
2.2 人工蜂群算法求解RCPSP
本文ABC算法的基础采用基于优先权编码的人工蜂群算法对RCPSP进行求解。
2.2.1 基于优先权的食物源位置编码
在ABC算法中,每个食物源的位置代表一个可行解。在用ABC算法求解资源受限项目调度问题时,每个食物源的位置xi是一个n维向量,取xi=(xi1,xi2,…,xid,…,xin),向量的维数n即是项目的非虚拟任务数。食物源xi代表一种项目任务的优先权序列。其中,xid是第i个食物源的第d个位置的值,它对应了第d项任务的优先权为xid。ABC算法得到的xi是连续数构成的向量,通过把xi向量元素按从小到大排序,转换成1~n的整数排列。这种整数优先权序列再通过调度生成机制转换为一个可行的调度方案。
2.2.2 适应值函数
ABC算法中食物源的好坏用蜂蜜量的多少来衡量,蜂蜜量是指食物源对应的可行解的适应值函数。在RCPSP中食物源对应了项目任务的优先权序列,优先权序列可以通过调度生成机制转换成可行调度方案,每一调度方案对应了项目工期。RCPSP优化目标是使项目工期最短,并意味着解的质量越好,因此ABC算法中食物源xi的适应值fiti。可由式(4)转换得到。

2.2.3 扩展串行调度生成机制
一个食物源的位置编码对应了项目的一种任务优先权序列,需要通过适当的调度生成机制把任务的优先权转化为可行的调度方案,本文采用扩展的串行调度生成机制[5]来生成可行调度方案。串行调度有两种对齐调度方式,一种是左齐计划,一种是右齐计划。所谓扩展的串行调度机制就是采用双齐计划进行调度,实现过程分为:(1)采用串行调度方法生成一个左齐计划;(2)在左齐计划的基础上,以左齐计划的结束任务完工时间为基准,再生成右齐计划;(3)若右齐计划开始任务开始时间大于零,则整个右齐计划同步左移至开始任务最早开始时间为零,即再进行一个左齐计划。通过这一调度机制就可以实现将食物源的解转换为可行的调度方案。
2.2.4 算法的实现步骤
ABC算法求解RCPSP的实现步骤如下:
(1)初始化。ABC算法首先产生初始种群,种群数量为SN,也代表SN个解(食物源)。每一个解xi(i=1,2,…,SN)对应了一组任务优先权序列,通过扩展的串行调度生成机制得到可行的调度方案,计算出每个xi的适应值fiti。
(2)迭代过程。在初始化之后,进入迭代(C=1,2,…,Cmax)过程,Cmax为最大迭代次数。在每次迭代中,三种类型的人工蜂执行不同的操作,种群的全局最优解就随着人工蜂群每次迭代中所寻找的食物源适应值的情况不断更新。
①工作蜂有SN个,对应SN个食物源,工作蜂i的食物源为xi,工作蜂i在种群中随机选择一个工作蜂k做它的邻居,并在工作蜂k的食物源xk的n维向量中随机选择一位d(d=1,2,…,n)。vi为工作蜂i的候选食物源,vi与xi除了第j位vid外,其余各位和xi一致。vid的计算方法为:

其中,fiti为工作蜂i的食物源的适应值。跟随蜂j通过轮盘赌的形式从工作蜂的食物源中选择食物源,假设工作蜂i的食物源xi被选中,跟随蜂j采用和①相同的方法来生产侯选食物源vi,同时采用和①相同贪婪策略在vi和xi之间进行取舍,traili的设置方法亦同上。
③当某一食物源xi的traili等于最大重复使用次数的限定值时,侦查蜂就会随机生成一个新的食物源取代xi,原来的食物源被舍弃不用。
(3)结束。当步骤(2)完成Cmax次迭代后,ABC算法结束,输出最优调度方案及项目最短工期。
3 仿真实验
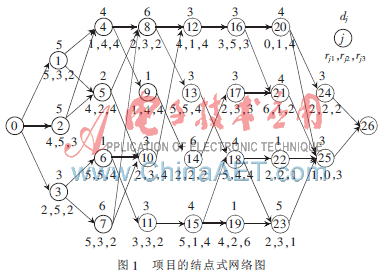
为了验证ABC算法求解RCPSP的有效性,本文选取的算例为项目的结点式网络图[6],如图1所示,项目的任务集为J={0,1,2,…,25,26},任务0和26为虚任务。项目的可更新资源种类为三种,每种资源在单位时间内大最大使用限额为6。图1中,结点圆圈内数字为任务编号,结点上方数字为任务工期,结点下方数字分别为该任务对三种资源的使用量。
ABC仿真实验选取蜂群数量NP=20,即食物源SN=10,最大迭代次数Cmax=50,工作蜂生成候选食物源应用式(5)时,取参数ω1=0.7;跟随蜂寻找候选食物源应用(5)式时,取参数ω2=1。图2给出了ABC算法在迭代中得到的项目工期的收敛过程,项目的工期的最优解为64天,所得的最优结果与参考文献[5]一致,同时与参考文献[5]比较来看,由于采用了扩展的串行调度生成机制,初始解离最优解距离更近。

图3给出了应用ABC算法得到的本算例最优调度时的甘特图。图4给出了此时项目可用资源的利用情况图,由图可见,在最短项目工期为64天的情况下,各任务在执行过程中满足三种资源的限制。

本文针对资源受限的项目调度优化问题的数学模型,提出了一种基于优先权编码的人工蜂群算法,通过扩展的串行调度生成机制将优先权编码转换为可行的调度方案。实际算例仿真结果表明,人工蜂群算法能够有效地求解资源受限的项目调度问题,算法的收敛速度较快,精度较高。既提高了算法的优化效率,又提高了算法的优化精度,同时扩展调度机制与串行调度生成机制相比具有明显的优点。
参考文献
[1] BLAZEWICZ J, LENSTRA J K, RINNOOY K A H G. Scheduling subject to resource constraints: classifcation and complexity[J]. Discrete Applied Mathematics. 1983,5 (1):11-24.
[2] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report-TRO6, 2005.
[3] KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007,39(3): 459-471.
[4] KARABOGA D, BASTURK, B. On the performance of artificial bee colony(ABC) algorithm[J]. Applied Soft Computing. 2008,8(1):687-697.
[5] Deng Linyi, Lin Yan, Chen Ming. Hybrid ant colony optimization for the resource-constrained project scheduling problem[J]. Journal of Systems Engineering and Electronics 2010,21(1):67-71.
[6] Zhang Hong, Li Heng, TAM C M. Particle swarm optimization for resource-constrained project scheduling[J]. International Journal of Project Management 2006,24:83-92.

