摘  要: 提出了一种基于粗糙集的决策规则挖掘算法。该算法主要包括属性归约、元组合并、规则提取和规则评估。最后用一个实例说明了算法的有效性。

　　关键词: 粗糙集  属性归约  决策规则  数据挖掘

　　粗糙集是一种处理不精确与不完全数据的新的数学理论。粗糙集理论建立在分类机制的基础上,将知识理解为对数据的划分,是在特定空间上由等价关系构成的划分。近年来,它已被广泛地应用在人工智能、模式识别和数据挖掘等方面。

　　一个决策信息系统(本文假定决策信息系统是相容的)包含了某一领域中大量实例(元组)信息,是领域的实例数据库。它记录了大量实例的属性值和决策情况,是领域知识的载体。数据挖掘的目的就是要通过分析这个实例数据库来获得该领域中事先未知的、潜在有用的和最终可理解的规律性知识。决策信息系统中的一个实例(元组)就代表一条基本的决策规则。如果把所有这样的决策规则罗列出来,就可以得到一个决策规则的集合。但是,这样的决策规则的集合是没有任何用处的。因为其中的决策规则没有适应性,只是机械地记录了一个实例的情况,而不能适应其他新的情况。为了从决策信息系统中挖掘出适应性较大的决策规则,本文提出了一种基于粗糙集的决策规则挖掘算法。实践证明,运用该算法挖掘得到的决策规则具有较高的适应性,能代表一类具有相同规律特性的实例,并可以在今后的决策过程中利用这些决策规则对未知的观察实例进行决策判定。

1 粗糙集的理论基础

　　(1)信息系统

　　一个信息系统定义为四元组:S={U,Q,V,f}。其中:U为对象集,即论域;Q=CYD为属性的集合;V为各属性的值域;f为U×Q→V的映射,它为U中各对象的属性指定惟一值。

　　(2)分辨矩阵

　　信息系统S中关于属性集C的分辨矩阵M(C)=(m_i,j)_n×n定义为:

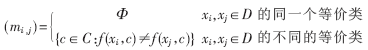
　　M(C)=(mi,j)_n×n代表了区分x_i,x_j的完整信息,它是对称矩阵,所以只需计算m_ij(1≤j≤i≤n)。

　　(3)核  心

　　相对于属性集D,属于属性集C的所有归约的交集属性的集合为属性集C的核心,记为CORE(C,D)。用核心作为计算归约集的起点,可以简化属性归约集的计算。为简化计算核心,一般通过分辨矩阵进行。具体计算的公式如下:

CORE={c∈C:m_ij={c},对于所有1≤j≤i≤n

　　(4)不可分辨关系

　　对于任何一个属性集合P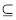Q,不可分辨关系用IND表示,其定义如下:

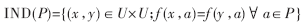
　　如果(x,y)∈IND(P),则x、y称为相对于P是不可分辨的。不可分辨关系实际上就是U上的等价关系。因此,针对属性集P上的不可分辨关系,U可划分为几个等价类,用U/IND(P)表示。

　　(5)下近似集

　　对任何一个对象子集X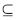U和属性子集P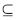Q,P的下近似集为:

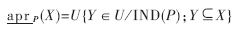
　　(6)属性的依赖度

　　在属性归约中,利用二个属性集合P、R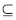Q之间的相互依赖程度,可以定义一个属性α的重要性。属性集P对R的依赖程度用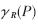表示。其定义如下:

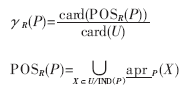
　　其中:card()表示集合的基数,POS_R(P)是属性集R在U/IND(P)中的正区域。

　　(7)属性的重要性

　　不同属性对于决定条件属性和决策属性之间的依赖关系起着不同的作用。属性α加入属性集R,对于分类U/IND(P)的重要程度定义为:

　　属性α的重要性是相对而言的,它依赖于属性P和R。因此,在不同的背景下,属性的重要性可能不同。如果决策属性定义为D,则SGF(α,R,P)反映的是将属性α加入属性集R中以后,R与D之间的依赖程度的改变,从而体现出属性α的重要性。

2  算法的基本步骤

　　运用该算法来挖掘隐含在决策信息系统中的决策规则的基本步骤包括:属性归约、元组合并、规则提取和规则评估。

　　(1)属性归约。属性归约是粗糙集理论中的一个重要的研究课题。通常,决策信息系统中的属性并非同等重要,且存在冗余,这不利于做出正确而简洁的决策。属性归约是在保持决策信息系统的分类和决策能力不变的前提下,删除不相关或不重要的属性。因此,在进行属性归约时,人们总希望找到属性的最小约简,但这是一个NP难度的问题。幸运的是,在大多数情况下,无需找出属性的最小约简,因为用户只对与处理任务相关的最佳子集感兴趣。根据属性之间的依赖关系、重要性等,可以比较容易且有效地找出一个最佳归约集。下面给出了计算最佳归约集的算法。该算法以核心作为计算的起点,每次选择重要性最大的属性加入属性集REDU,在步骤④的前向选择结束后,属性集REDU已包含了一些起重要作用的属性,且没有改变原始属性集与决策属性之间的依赖程度。最后的反馈过程是从属性集REDU中逐个去掉属性。如果去掉该属性会造成依赖度变化,则恢复该属性,否则删除该属性。最后剩下的属性集就是最佳归约集。删除决策信息系统中不属于最佳归约集的属性就可得到最佳属性归约的决策信息系统。

　　算法:计算最佳归约集

　　输入:一个具有条件属性集C和决策属性集D的相容决策信息系统S。

　　输出:一个最佳归约集。

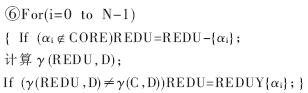
　　(2)元组合并。合并最佳属性归约的决策信息系统中的元组分二个步骤。首先,如果多个(二个或二个以上)元组的各个条件属性和决策属性都一一对应相同,则将这多个元组合并成一个元组;其次,如果多个元组的决策属性相同,条件属性只有一个不同,并且这多个元组在该条件属性上的取值覆盖了它所有可能的值,则将这多个元组合并成一个元组,并且将该条件属性从该元组中删除。最终便可得到最简决策信息系统。

　　(3)规则提取。尽管由上述步骤得到的最简决策信息系统已经可以为决策者提供正确而简洁的决策,但用这种方法表示决策知识的可读性很差,不易被人理解,尤其是当生成的最简决策信息系统仍然较大时。因此,有必要提取出隐含在其中的决策规则,并以IF-THEN的形式表示出来。其具体方法是:对于简化的决策信息系统中的每一个元组,将它的每一个条件属性的属性-值对形成规则前件(IF部分)的一个合取项;将它的每一个决策属性的属性-值对形成规则后件(THEN部分)的一个合取项。最终便可得到用IF-THEN形式表示的决策规则集。

　　(4)规则评估。对于特定的决策者来说,他不一定对上述生成的所有决策规则都感兴趣。因此,决策者需要根据自己的目标进一步限制挖掘过程产生的不感兴趣的决策规则的数量。这可以通过设定规则兴趣度度量方法来实现。规则兴趣度度量的方法很多,其中最常见的方法有支持度度量和置信度度量。只有那些支持度和置信度都大于或等于决策者事先设定的最小支持度阈值和最小置信度阈值的决策规则才被认为是有趣的。对于形如“A?圯B”的决策规则,其支持度和置信度的定义分别为:

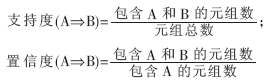
3 算法的应用实例

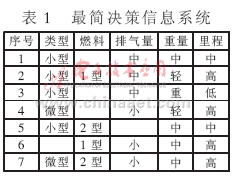
　　表1(见参考文献[3])给出了一个关于汽车信息的决策信息系统(系统是相容的)。其条件属性C={类型、汽缸、涡轮式、燃料、排气量、压缩率、功率、换档、重量},决策属性D={里程}。挖掘的目标是提取出隐含在该相容决策信息系统中的被决策者感兴趣的实际决定汽车里程的决策规则。运用算法的第(1)、(2)步可以得到如表1所示的最简决策信息系统;运用算法的第(3)、(4)步可以得到如表2所示的决策规则集。假如某一决策者设定最小支持度阈值和最小置信度阈值分别为15%和90%,则表2中的所有规则中就只有规则1、5、6是有趣的。

4 结束语

　　随着KDD和DM的兴起,粗糙集方法正赢得越来越多的研究者的青睐,并在各个领域获得了广泛的应用。究其原因有:①KDD和DM的对象多为关系数据库,其中就有许多可视为粗糙集理论中的决策信息系统,这给粗糙集方法的应用带来了极大的方便。②现实世界中的规则有确定性的,也有不确定性的。从数据库中发现的不确定性的规则为粗糙集方法提供了用武之地。③基于粗糙集的挖掘算法有利于并行执行,可以极大地提高挖掘效率。④粗糙集方法能够自动地选择合适的属性集,去掉多余的属性,提高挖掘的效率。⑤与其他方法相比,用粗糙集方法得到的决策规则更易验证和检测。

参考文献

1  刘同明.数据挖掘技术及其应用.北京:国防工业出版社,2001

2  王国胤.Rough集理论与知识获取.西安:西安交通大学出版社,2001

3  代建华.一种基于粗糙集的决策系统属性约简算法.小型微型计算机系统,2003;24(3)

4  Kryszkiewicz M,Rybinski H.Reducing Information Systems with Uncertain Attributes.In:9th International Symposium on Foundations of Intelligent Systems,1996