摘 要: 在传统的DES加密算法的基础上,提出一种对密钥实行动态管理的硬件设计方案,给出了其FPGA实现方法。通过对DES加密原理的分析,利用其子密钥的生成与核心算法相关性较弱的特点,对密钥进行重新配置。DES算法采用资源优先方案,在轮函数内部设置流水线架构,提高了整体处理速度;在FPGA上实现轮函数和密钥变换函数独立运算,减少了相邻流水线级间的逻辑复杂度,从而实现了DES算法在FPGA条件下的重构设计。最终通过对设计结果的功能仿真和测试分析,论证了整个设计的正确性。
关键词: DES; 移位寄存器" title="线性反馈移位寄存器">线性反馈移位寄存器; 混沌加密; FPGA
随着密码学技术的飞速发展,软件加密已经非常流行,但由于硬件加密的稳定性和兼容性更好而且速度更快,所以仍是商业和军事用途的主要选择。而FPGA在实现算法方面具有灵活性、物理安全性和比软件更高的速度性能,已成为硬件实现加密算法的最好选择。
数据加密标准[1]DES(Data Encryption Standard)是迄今为止世界上最为广泛使用的一种分组密码算法。本文提出了一种密钥可配置的DES算法的FPGA实现方案:即在传统DES算法的基础上,采取密钥可配置的方法,增加密钥复杂度,加强密钥保护,利用初始密钥选择的随机性,增强算法抗攻击能力,通过选择多种密钥产生方法,进行DES加密。因此,即便知道了密文和密钥,由于不知道采取何种密钥产生方式,仍然难以攻破。
1 加密算法理论
1.1 DES算法原理
数据加密标准DES算法是用于计算机数据加密保护的分组加密的数学算法,算法以64 bit为一个分组对数据进行加密。使用64 bit的密钥加密64 bit分组的信息。首先将原始数据64 bit明文进行初始置换IP,然后与子密钥(由加密密钥产生)进行一系列迭代运算,最后再经过逆置换IP-1,即可得到64 bit密文(加密后数据)。在每一轮中,数列块的右边32 bit数据和密钥(Key)一起传送给函数f,函数f运算的结果再与数列块左边32 bit数据进行“异或”操作。其中S盒(S选择函数)是DES算法的心脏,由它实现非线性变换。
解密过程与此类似,只是在应用子密钥时,顺序颠倒为k16,k15,…k2,k1。图1所示为DES加密原理。从图中可以看到轮密钥产生器相对于DES算法是独立运算的,这就为密钥的配置提供了可能和便利。

因为该算法是公开的,因此64 bit的密钥算法是极其重要的,因为它是导致由64 bit的明文到64 bit密文唯一集合的密码运算。故DES的加密安全依赖于对密码的保护。
1.2 线性反馈移位寄存器
线性反馈移位寄存器LFSR(Linear Feedback Shift Register)如图2所示,是一种非常成熟的序列生成方法,已被广泛地应用于密码技术、通信技术等方面。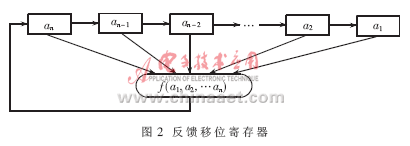
若反馈函数为线性函数f(a1,a2,…an)=c1a1 c2a2
c2a2 …
… cnan,则称为线性反馈移位寄存器(LFSR)。其中,a1,a2,…an为二值(0,1)存储单元,这n个二值存储单元称为该反馈移位寄存器的级。任一时刻,这些级的内容构成反馈移位寄存器的状态,每个状态可以用n长序列(a1,a2,…an)来表示,对应1个GF(2)域上的n维向量。反馈函数f(a1,a2,…an)是n元布尔函数。在时钟脉冲的控制下,每经过1个时刻,每一级存储器ai都要将自己存储的内容向下一级ai-1传递,反馈函数由存储器当前状态计算出an下一时刻的内容。
cnan,则称为线性反馈移位寄存器(LFSR)。其中,a1,a2,…an为二值(0,1)存储单元,这n个二值存储单元称为该反馈移位寄存器的级。任一时刻,这些级的内容构成反馈移位寄存器的状态,每个状态可以用n长序列(a1,a2,…an)来表示,对应1个GF(2)域上的n维向量。反馈函数f(a1,a2,…an)是n元布尔函数。在时钟脉冲的控制下,每经过1个时刻,每一级存储器ai都要将自己存储的内容向下一级ai-1传递,反馈函数由存储器当前状态计算出an下一时刻的内容。
由于线性反馈移位寄存器易于构造且易于应用软件和数字硬件实现,所以密码设计者常用它来构造序列密码。本文采用线性反馈移位寄存器作为对初始密钥的一种配置。
1.3 混沌密码
由于混沌系统具有的宽频谱、类随机特性、对结构参数及初始状态的极端敏感性等性质,日益成为密码学的重要分支。混沌密码在硬件实现时,应该在尽量提高精度、逼近混沌特性的同时,提高运算速度,满足工程中实时处理的要求。而一维Logistic映射从数学形式上来看是一个非常简单的混沌映射,但此系统具有极其复杂的动力学行为,在保密通信领域的应用十分广泛[2]。因此本设计就采用了Logistic映射对密钥进行混淆。
Logistic映射是混沌模型中的一种,它是一个离散混沌系统,表达式为:xn+1=u×xn×(1-xn),(n=1,2,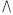 ),其中初始值x0∈(0,1)。混沌动力系统的研究指出,当3≤u≤4时,Logistic映射由出现倍分岔现象逐步趋于混沌状态[3],即由初始条件在Logistic映射的作用下所产生的{xn,n=0,1,2,
),其中初始值x0∈(0,1)。混沌动力系统的研究指出,当3≤u≤4时,Logistic映射由出现倍分岔现象逐步趋于混沌状态[3],即由初始条件在Logistic映射的作用下所产生的{xn,n=0,1,2,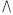 )是非周期、不收敛的,且对初始值非常敏感的混沌序列。当u=4时,表达式为:xn+1=4×xn×(1-xn), 此时构成的动态系统在连续域上是混沌的,x0取(0,1)内的值。
)是非周期、不收敛的,且对初始值非常敏感的混沌序列。当u=4时,表达式为:xn+1=4×xn×(1-xn), 此时构成的动态系统在连续域上是混沌的,x0取(0,1)内的值。
2 FPGA上的算法实现
采用基于SRAM技术的FPGA设计的电路虽然不具有保密性,但是基于Kerckhoff原则,所实现算法的硬件电路是可行且安全的。为了增强DES算法的安全性,本文提出了对密钥进行动态配置来改进DES算法,利用线性反馈移位寄存器和Logistic映射增加初始密钥的复杂度。具体配置方法为:根据控制信号,将输入的64 bit密钥进行配置,既可以直接将初始密钥引入,参与DES加密算法,又可以经过线性反馈移位寄存器,得到新的密钥流参与DES加密算法,还可以经过混沌加密进一步增强DES算法的密钥安全性。
2.1 密钥流生成器的选取
本设计中,选取线性反馈移位寄存器和混沌序列作为密钥流生成器。
由于N级线性反馈移位寄存器输出的序列是周期性的,非常适合硬件实现,且最大周期为2n-1,为了产生64 bit的密钥序列,设计5级移位寄存器(周期为31),其状态关系为:
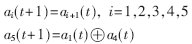
这样无需等64个时钟周期,只需31个周期就可以得到64 bit的密钥。
为了从混沌序列中获得每轮64 bit的轮密钥,需要对产生的混沌序列进行有限精度的二进制编码,即把混沌序列中的每一项与一个定长的二进制编码相对应。当u=4时,量化后的表达式为:
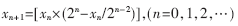
初始值x0为(0,2n-1)之间的整数,取n=16 bit,使用映射函数把4个连续的序列项映射成1个轮密钥,即rkey={key1,key2,key3,key4}。这样产生的轮密钥既有随机性又有独立性。
2.2 硬件实现结构
传统的DES算法主要有2组输入信号:明文datain[63:0]、密钥keyin[63:0];2组输出信号:密文dataout[63:0]以及有效信号dataout_en。为了实现对密钥的配置,增加了密钥选择输入信号key_sel[1:0]:当取00或者11时,直接将密钥keyin送至DES模块中的密钥产生模块;当取01时,将密钥keyin先送至线形反馈移位寄存器中生成新的序列密码作为新的密钥送至密钥产生模块中;当keyin取10时,将密钥keyin先送至混沌加密模块中生成新的混沌序列作为新的密钥参与后续的加密运算。这2个模块不可能同时工作,当其中1个工作时,另1个关闭时钟。采取关闭时钟法选择对应的加密算法,既能简化电路,减少控制信号,减少门的翻转次数,又能降低芯片集成度,进而达到降低功耗的目的。其逻辑结构如图3所示。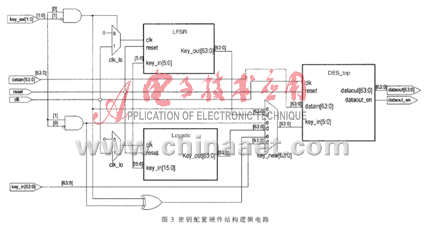
为了有效地控制密钥生成模块的工作,同时降低系统功耗,本设计采用了FPGA设计中的乒乓操作技巧[4],具体操作为:对线性反馈移位寄存器(LFSR)和混沌加密模块(logistic)分别使用独立的时钟信号clk_lf、clk_lo,而不使用系统时钟clk。通过密钥选择输入信号key_sel的取值不同,使clk_lf和clk_lo的值分别等于0或是系统时钟clk。
DES加密算法作为本设计中的核心算法,以多轮的密钥变换轮函数、密钥和数据运算轮函数为特征,相应的硬件实现方法有2种:一种是通过轮函数的16份硬件拷贝,达到深度细化的流水线处理,实现性能最优;另一种是通过分时复用,重复调用1份轮函数的硬件拷贝,以时间换空间,从而得到硬件资源占用的最小化。
本设计采取的是资源优先方案:即仅用硬件实现一套密钥变换和密钥加数据运算轮函数,通过反复16次调用这一硬件结构来实现1次DES加密运算。这样可以大大减少了硬件开销,但芯片的性能有所降低。因此,又采取在轮函数内部设置一级流水线来提高整体处理的速度。在硬件上实现数据加密钥轮函数和密钥变换函数的同步流水线架构,减少了相邻流水线级间的逻辑复杂度,通过设置轮计数器对所进行的轮运算计数,控制数据选择器,从而实现轮函数复用。其硬件结构如图4所示。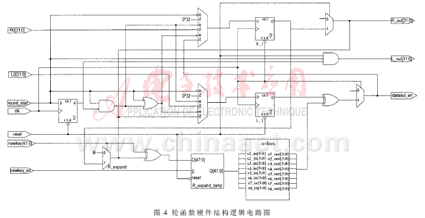
3 仿真及验证
本文所有算法均采用Verilog HDL实现,并在Modelsim仿真环境下,编写了测试激励,进行RTL级功能仿真,如图5所示。由图可以看到,此时key_sel和arith_sel输入为1时,密钥流采取了混沌加密,算法采用了DES算法,输入明文为:636F6D7075746572,密钥数据为7365637572697479,经过组合加密后得到的密文为49D28E37281FFFB2。
行为级仿真通过后,又采用了FPGA专用综合工具Synplify对算法进行了综合。结果表明:该组合加密模块耗费3 056 LE,该模块下载到Virtex-II芯片中,最高工作频率可达50 MHz。由于本设计采用16级流水总线设计,所以最高数据编码/解码速率可达3 Gb/s。综合完成后,又使用XILINX的ISE软件进行布局布线,并提取了网表和延时文件,在Modelsim后仿其环境中进行了时序后仿真,结果完全符合时序要求,达到了设计目的。
加密数据的安全不仅依赖于加密算法的保密,更依赖于加密密钥的安全。本文通过对整个加密算法的分析,提出了较为合理的密钥动态配置的DES加密算法的设计方法和实现途径,并在FPGA平台上进行了测试和验证,数据的连续加/解密传输达到了预先的设计要求。这种实现方法整体处理速度高,相邻流水线级间的逻辑复杂程度低,程序对编译器的依赖性少,提高了算法的整体性能。通过适当改进,可以设计出通用型芯片,实现对通信数据的实时、可靠加密传输,在通信、军事、加密等领域有着广泛的应用前景。
参考文献
[1] 卢开澄.计算机密码学(第三版). 北京:清华大学出版社,2003.
[2] 姜丽, 金卫雄. 混沌加密技术及算法的研究.淮海工学院学报, 2004,13(4):39-42.
[3] 吕金虎,陆君安,陈士华.混沌时间序列分析及其应用.武汉:武汉大学出版社, 2002.
[4] 华清软件嵌入式培训中心.FPGA应用开发入门与典型实例.北京:人民邮电出版社,2008.

