摘 要: 在实验的基础上通过对现有的二值化算法进行研究分析, 提出了一种新的二值化算法。该算法利用形态学的开运算来消除图像光照不均匀，根据最大类间方差确定图像阈值，然后高斯平滑噪声，锐化边缘。结果表明该算法能较好地保留图像特征，并且能够克服传统方法带来的离散噪声，二值化效果较好。
　　关键词: 光学字符识别;数学形态学;二值化;熵

　　目前，光学字符识别OCR(Optical Character Recognition)技术已在众多领域得到广泛应用。它作为计算机智能接口的重要组成部分，能够实现文字信息高速、自动地输入。在字符图像识别方面，预处理效果的好坏直接影响OCR系统的性能，其中二值化更是整个预处理过程的关键所在。尽管近年来各位研究人员提出了许多二值化方法[1,2]，但是到目前为止还没有一种通用的方法，也不存在一个判断二值化是否成功的客观标准，因此它被认为是计算机视觉中的一个瓶颈。
　　本文提出了一种基于灰度形态学的处理方法：提取图像的背景，用原图减去背景使其变成零背景图像，接着采用最大类间方差法确定阈值进行二值化。实验结果表明了算法的有效性，适用于字符识别的预处理。本实验的全部程序在Visual Studio 2005.NET环境下开发实现，源代码用C++语言编写[3,4]。
1 基本原理
1.1 数学形态学图像处理^[5,6]
　　数学形态学是一门新兴的图像处理分析工具，在图像分析中得到了广泛的应用。通常情况下，形态学处理以在图像中移动一个结构元素并进行一种类似于卷积操作的方式进行。数学形态学由一系列代数算子组成，基本的算子包括腐蚀、膨胀以及由这两种运算组合而成的开运算和闭运算。图像B和结构元素S都是定义在二维笛卡尔网格上的集合。当一个结构元素的原点平移到点(x,y)处时，将其记为Sxy。
　　

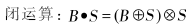
　　由形态学的运算可知，开运算可以去除较小的明亮细节并保持较大的明亮区域不变；闭运算用于去除图像中的暗细节部分而保持明亮细节不受影响。由于背景表现为图像中的高频部分，因此可采用开运算进行背景估计，然后从原始图像中减去背景[7]。本文正是用这个方法去除背景得到零背景图像，去除背景可能不均匀所带来的影响[8]。
1.2 最大类间方差法
　　最大类间方差法[9,10]是由日本学者大津于1979 年提出的，是一种自适应的阈值确定方法，又叫大津法，简称Otsu。它按图像的灰度特性，将图像分成背景和目标两部分。因方差是灰度分布均匀性的一种度量，方差值越大，说明构成图像的两部分差别越大，因此，背景和目标之间的类间方差越大，说明构成图像的两部分的差别也越大。当部分目标错分为背景或部分背景错分为目标都会导致两部分差别变小，因此，使类间方差最大的分割意味着错分概率最小。设t为前景与背景的二值化阈值；属于前景像素点数占图像比例为w₀，平均灰度为u₀；背景点数占图像比例为w₁，平均灰度为u₁；图像的总平均灰度为u，类间方差记为g。假设图像的背景较暗，图像的大小为M×N，图中像素的灰度小于阈值t的像素个数为N₀(此类像素被判为前景)，像素灰度值大于阈值t的像素个数为N1(此类像素被判为背景)，则有：

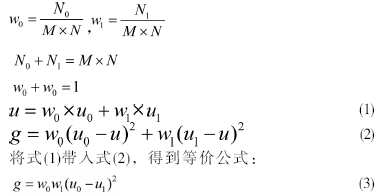
　　采用遍历的方法得到使类间方差最大的阈值t，即为所求。
1.3 最大熵法^[7]
　　熵是作为函数不确定性的度量，将熵的概念引入图像二值化处理中，就是基于图像灰度直方图的熵测量。通常，可以从不同的角度出发来定义不同的图像灰度直方图的熵测量方法，在此基础上定义获得最大熵以及选择最佳二值化阈值的方法。一般情况下，有3种基于图像灰度直方图熵测量的图像二值化处理阈值法：基于一个分布假设提出的P氏熵法、基于2个分布假设提出的KSW 熵法以及基于极小类间依赖性的JM熵法。
　　下面，本文将重点讨论基于2个分布假设提出的KSW熵法。 
　　

2 本文算法的基本原理与步骤
　　本文提出了一种基于数学形态学的文本图像二值化算法，首先用形态学开运算得到零背景图像，然后将Otsu算法用于零背景图像，确定阈值t^*。由于此时二值化图像中出现离散杂点，故用高斯平滑来消除这些杂点，最后用拉普拉斯锐化来增强图像。算法的具体过程描述如下：
　　(1)导入目标图像A；
　　(2)选取一个大的结构对目标图像A进行多次开运算提取图像背景；
　　(3)原图像减去背景，得出背景为0的图像B；
　　(4)对B进行Otsu法处理，得出最优阈值t^*；
　　(5)根据t^*对图像B二值化分割形成图像C；
　　(6)对图像C进行平滑滤波形成图像D；
　　(7)对图像D进行拉普拉斯锐化形成最终的二值图像E。
　　上述算法考虑了图像光照不均匀、噪声干扰等情况，采用了大结构提取背景对算法的性能影响不大。
3 实验结果及分析 
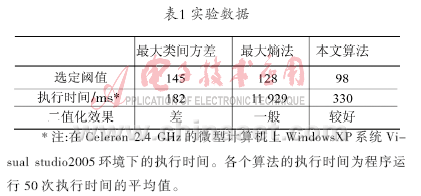
　　为了检验本文算法的有效性，采用一段旧报纸图像作为测试图像进行实验并与采用最大类间方差法和最大熵法[6]进行比较，实验结果如图1所示，实验数据如表1所示。图1(b)中因目标与背景灰度差不多而出现多块的黑色区块；图1(c)效果比图1(b)好，没有了黑色区块，但有一部分背景被视为目标，有大量的离散噪声，二值化效果没有图1(d)好；图1(d)中没有黑色区块且离散噪声也要少很多。从表1可以看出，在执行速度方面，本文算法比最大类间方差算法慢，但比最大熵法要快得多，因为本文算法虽然中间有一个提取图像背景的过程，但在这个过程中选择的开运算的结构元素相当大，执行时间相对整个过程是很短的，而最大熵由于涉及到对数运算，速度当然就慢得多。

　　本文重点分析了最大类间方差法[9]和KSW最大熵法[7]在处理低质量文本图像二值化时存在的问题，在此基础上，基于数学形态学原理，提出了一种基于形态学的文本图像二值化算法。实验结果证明了该算法的可行性。该算法克服了最大类间方差法出现的黑块并使得离散噪声较最大熵法有较大改善。但是，在实验过程中发现，对噪声较大、复杂、甚至变形的文本图像，其二值化效果不是很理想，这也将成为下一步努力的方向。
参考文献
[1]  陈丹, 张蜂, 贺贵明. 一种改进的文本图像二值化算法[J]. 计算机工程, 2003, 29(13): 85-86.
[2]  朱军民, 黄磊, 刘昌平. 图像二值化方法比较[A]. 第八届全国汉字识别学术会议论文, 绍兴，2002.
[3]  杨淑莹. VC++图像处理程序设计[M]. 北京: 清华大学出版社, 2005.
[4]  陈纯. 计算机图像处理技术与算法[M]. 北京:清华大学出版社, 2003.
[5]  崔屹.图像处理与分析—数学形态学方法及应用[M]. 北京: 科学出版社, 2000.
[6]  CASTLEMAN K R . 数字图像处理[M]. 北京: 电子工业出版社, 2006.
[7]  魏军伟, 方敏. 基于最大熵和形态学的边缘检测[J]. 计算机工程与应用，2007,43(21)：70-71，92.
[8]  潘梅森, 张奋, 霍超阳. 一种车牌号码图像二值化的新方法[J]. 计算机工程， 2008，34(4):209-211,214.
[9]  齐丽娜, 张博. 最大类间方差法在图像处理中的应用[J]. 无线电工程, 2006(7): 29-30,48.
[10] RAIS N B, HANIF M S, TAJ I A. Adaptive thresholding technique for document image analysis[C]. Multitopic Conference, 2004. Proceedings of INMIC 2004. 8th International, 2004: 61-66.