摘 要: 以蚁群算法为基础,设计了基于蚁群算法的物流配送路径优化模型,通过实验表明了该方法的可行性,且基于蚁群算法的优化模型比其他算法模型具有更好的优化效果和更高的稳定性。
关键词: 电子商务;路径优化;TSP;蚁群算法
电子商务是在Internet上基于浏览器/服务器(C/S)模式实现消费者网上消费的一种新型的商业运营模式。电子商务中的任何一笔交易,都包含着基本的信息流、商流、资金流和物流[1]。其中物流作为有形商品实现网络交易的重要支持环节,对企业起着举足轻重的作用。 物流配送的效率已经成为制约我国电子商务快速发展的一个重要瓶颈,因而如何优化和完善物流配送线路,提高企业市场竞争力是电子商务企业成功的关键之所在。本文以蚁群算法为基础,采用Matlab实现的模型来研究蚁群算法在电子商务物流配送线路优化方面应用的可行性,并将结果与其他算法进行比较。
1 问题分析
电子商务企业的货物配送路径问题实际上就是求最小配送成本问题,但由于要考虑人力、物力等问题的模拟过于复杂,因此为了能从最简单的方面考虑,本研究只考虑路程和运费组成的最小成本问题。由于目前运费成本是一定的,从而可转化为求最短路径问题。在二维空间可描述如下[2]:在配送图G(V,A)中,V表示所有要收货的客户集合,V=(v1,v2,…,vM),对G中的某一边(vi,vj),相应的有一个距离d(vi,vj),如果G中不存在边(vi,vj),则令d(vi,vj)无穷大,实际上是这两个客户所在的地点之间不存在通路。因此只要能在最短通路状态下把每个客户都走一遍,也就达到了费用最低的效果。可将这种配送最小成本的问题转化为求解一个相对复杂的旅行商问题(TSP)的最短路径。物流配送的数学模型就转变为[3]:

2 优化模型的设计
2.1 模型设计原理
蚁群算法是对蚂蚁觅食行为的模拟。现实蚂蚁存在于三维空间中,而优化问题位于二维平面中,因此首先将三维空间抽象为一个二维平面图。蚂蚁在连续平面运动,其运动轨迹总是离散点,计算机可以通过对离散点的处理组成连续的平面。现实蚂蚁在觅食过程中的前进方向主要由所处环境的信息素量来决定,在算法构造过程中,信息素被抽象为图的边上的轨迹,蚂蚁到达每一节点处根据边上的信息素浓度选择下一节点。蚂蚁从初始节点(巢穴)按照一定转移概率选择下一节点,最终选择行走到目标节点(食物源),这样便得到了TSP问题的一个可行解[4]。

(5)终止判断:判断循环次数Nc是否小于最大循环次数NcMax,如果尚未到达停止条件,则将所有禁忌表清空,并且重复步骤(2)~步骤(5),直到满足停止条件为止。
3 仿真实验
3.1 参数设置
本文分别采用蚁群算法、遗传算法以及禁忌搜索算法对30个城市的TSP问题进行比较研究。各算法的参数设置如下:
(1)蚁群算法:信息启发因子α=1,期望启发因子β=5,信息素挥发系数ρ=0.5,信息素强度Q=100,最大迭代次数NcMax=200,蚂蚁数m=30;
(2)遗传算法:初始种群inn=100,交叉概率为0.8,变异概率为0.8,最大迭代次数gnmax=1 000;
(3)禁忌搜索算法:禁忌长度t1=50,候选解l1=200,终止步数stop=1 000。
3.2 结果分析
采用Matlab语言实现三种算法模型对30个城市的TSP问题分别运行20次,表1给出了三种算法的运行结果,从表中可以看出,蚁群算法模型的运算结果最好、最稳定,运行时间也最短;遗传算法模型次之,它的稳定性和平均值要小于禁忌搜索算法;最禁忌搜索算法的最短路径长度最短,但整体稳定性最差。如图1~图6所示。
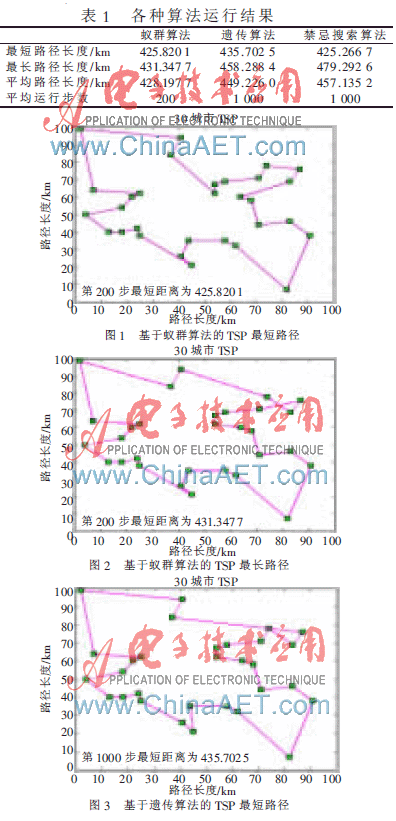
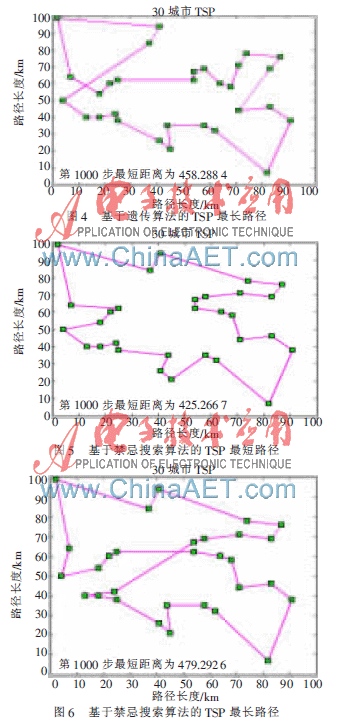
针对电子商务中的物流配送路径优化问题,将其抽象化为TSP问题,并采用蚁群算法为基础建立优化模型。随后介绍了优化模型的实现过程,通过实验,与遗传算法模型和禁忌搜索算法模型运行结果进行比较,结果表明,蚁群算法模型不但运行速度快,而且运行效果最好、最稳定,从而为电子商务中的物流配送路径优化提供了一种新的、可行的思路。
参考文献
[1] 朱立伟.现代化物流管理技术在电子商务中的作用[J].企业经济,2006(1):20-21.
[2] 温清芳.遗传算法求解TSP问题的MATLAB实现[J].韶关学院学报·自然科学,2007,28(6):18-22.
[3] 田贵超,黎明,韦雪洁.旅行商问题(TSP)的几种求解方法[J].计算机仿真,2006,23(8):153-157.
[4] 高阳.基于蚁群算法的集合覆盖问题求解及其应用研究[D].无锡:江南大学,2007
[5] 野莹莹,付丽君,程立英.基于MATLAB的蚁群算法仿真研究[J].装备制造技术,2008,(11):13-14.
[6] 熊芳敏,岑宇森,曾碧卿.运用蚁群算法解决物流中心拣货路径问题[J].华南师范大学学报(自然科学版),2010(2):50-54.
[7] 王军.蚁群算法求解TSP时参数设置的研究[J].科学技术与工程,2007,7(17):4501-4504.

