在TD-LTE系统中，Zadoff-Chu(ZC)序列主要应用于上行RS序列生成、PRACH前导序列生成以及主同步信号生成等[3]，它在整个TD-LTE系统中扮演着重要的角色，是建立上下行链路同步以及信道估计中不可或缺的一部分。Zadoff-Chu序列具有良好的自相关性和互相关性，这有利于减少不同前导之间的相互干扰，而且其本身具有对称性，这有利于减少序列生成的复杂度。同时LTE系统选择了素数长度的Zadoff-Chu序列，保证序列检测性能的提高。

    本文通过对ZC序列生成的分析以及自身的特性，结合理论推导，提出了一种简化的ZC生成算法的DSP实现方案，并通过仿真与比较，验证了该方案的可行性，能够满足LTE系统性能的要求。
1 Zadoff-Chu算法分析
    参数为u，序列长度为Nzc的ZC序列定义为：
    
    每计算一次Xu(n)的值，在求x的计算上就需要3次乘法和一次除法运算。对于长度为Nzc的序列而言，计算所有Xu(n)的指数x需要3×Nzc次的乘法和Nzc次的除法运算，然后利用式（2）计算每一个Xu(n)的值。
    用式(2)计算Zadoff-Chu序列的生成存在两点不足：(1)余弦和正弦运算属于一种非线性的运算，多次运算的复杂度很高，耗时很长，不利于满足LTE系统实时性的要求；(2)MS320C6000系列DSP在软件的实现中只能处理定点数运算，无法直接对浮点数进行处理。因而要利用式(2)计算必须对正弦和余弦进行量化处理。
    在定点DSP芯片中，采用定点数进行数值运算，其操作数一般采用整型数表示。一个整型数的最大表示范围取决于DSP芯片所给定的字长，一般为16 bit或32 bit。对DSP芯片而言，参与数值运算的数就是16 bit的整型数。通过设定小数点在16 bit数中的不同位置，就可以表示不同大小和不同精度的小数。数的定标有Q表示法和S表示法两种，如表1所示。

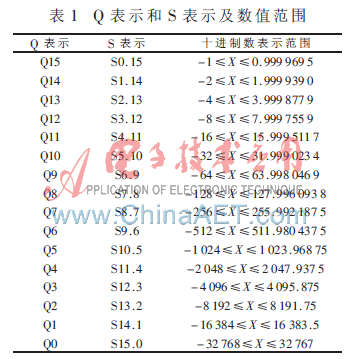
    从表1可以看出，不同的Q所表示的数不仅范围不同，而且精度也不相同。Q越大，数值范围越小，但精度越高；相反，Q越小，数值范围越大，但精度就越低。本文采用Q量化方法，浮点数与定点数的转换关系可表示为：浮点数(x)转换为定点数(xq)：xq=(int)x×2q
式中int表示下取整。由正弦和余弦的范围，结合表1可知，可以采用Q15进行浮点数到定点数的转化。为了减少正弦和余弦由于非线性造成的复杂运算，可以采用查表的方法。首先对sin(x)的0～π的值进行量化处理，根据sin(x)本身的对称性可以通过0～π的量化值取反得到；其次，根据正弦和余弦之间的关系cos(x)=sin(x+π/2)，可以将余弦值的求法转化到求正弦上。由于量化存在着误差，因而量化的点数越多，所求的值越接近理论上的值，但量化点数越大占用的内存空间也越大。在0～?仔在之间进行2 048点量化时，已十分接近理论值。因此采用0～π在之间进行2 048点量化。
    进一步对式（1）推导发现：
  
    由式（4）可知，对于给定的参数u，A(n)/A(n-1)为定值，对于初始值A(0)=1，XU(0)=1。通过式(3)和式(4)的递推关系就可以只通过乘法运算计算出ZC序列，在计算时只需要计算一次正弦和余弦即可。用这种方法将正弦和余弦转化成复数的乘法运算，减少了正弦和余弦归一化和量化查表的时间，进一步降低运算的复杂度。
    由ZC序列本身所具有的性质可知：
    

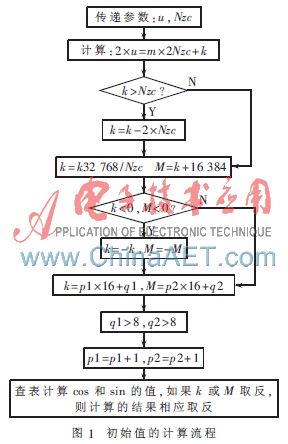
    首先把递推公式的初始值A(0)=1和Xu（0）=1分别用MVK指令赋值到相应的寄存器中。由递推关系式，首先计算出A（n），由于A（n-1）和计算出的旋转因子M均为复数，不能直接进行相应的乘法运算，只能采用复数相乘的法则。即A(n)的实部等于A（n-1）和M的实部与虚部分别相乘后再进行相减。为了减少指令的开销，可以采用DOTPN2指令，该条指令可以直接完成A(n-1)的实部和虚部与M的实部和虚部相乘之后相减，把得到的实部用SHR指令进行右移16 bit，保证得到的结果为半字。同样A（n）的虚部的计算，先用汇编指令PACK2交换M的实部和虚部，再用DOTP2指令完成A(n-1)和M的高16 bit和低16 bit的相乘以及A(n-1)和M的低16 bit和高16 bit的相乘之后再相加，同样用SHR指令对虚部的计算结果右移16 bit，保证虚部在半字的范围内。计算完成A（n）后，再把A（n）和Xu（n-1）进行复数相乘，从而得到Xu（n）的计算结果。由ZC序列本身所具有的对称性，分别将计算出的Xu（n）的实部和虚部用STH指令分别压栈到输出结果的第n个字和第Nzc-n-1个字中，至此ZC序列的计算全部完成。
3 性能分析与总结
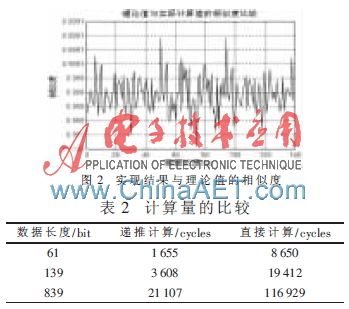
    通过DSP软件实现得到的结果与用MATLAB搭建的链路得到的理论数据进行比较，如图2所示。图2虽然只是长度Nzc=139点，但不失一般性。从图中可以看出，虽然量化误差的存在，但是在2 048点对sin在（0，π）区间进行量化时，得到的结果与理论数据的值相差在0.1%左右。同时在应用DSP软件实现中，尽量对程序进行优化，通过指令并行，操作码的合理设计以及减少或消除程序中的’NOP’指令[6]等方法进行优化。当运用TMS320C64×DSP芯片实现时，由于处理器的超高主频一般为1 GHz，所以一个指令周期耗时为1 ns，其运算速率非常快，如表2所示，与直接进行ZC序列的生成相比较大大降低了运算时间，可以满足LTE系统的快速有效性。

    本文从理论分析出发，根据TD-LTE系统特性以及Zadoff-Chu序列本身的性质，提出了一种简单有效的Zadoff-Chu算法实现方案，并将该算法在TMS320C64×芯片上实现。程序运行结果表明，提出的算法具有可行性和高效性，能够满足TD-LTE系统的需求。该方案已在LTE-TDD无线综合测试仪表的开发中得到了应用。
参考文献
[1] 丁玉美.数字信号处理[M].西安：西安电子科技大学出版社，2002.
[2] 何方白，张德民.数字信号处理[M].北京：高等教育出版社，2009.
[3] 3GPP TS 36.211 v9.0.0 Evolved universal terrest-rial  radio access(E-UTRA) physical channels and modulation (release 9)[S].2009-12.
[4] SAIDI A.Decimation-in-time-frequency FFT algorithm,  Manuscript，To be published.1993(8).
[5] Texas Instruments Incorporated.TMS320C64x/C6-4x+DSP.  CPU.and.Instruction.Set.Reference.Guide[E-B/OL].Http://www.ti.com.cn,2008.
[6] Texas Instruments Incorporated.TMS320C6000系列DSP编程工具与指南[M].田黎育，何佩琨，朱梦宇，译.北京：清华大学出版社，2006：32-50.
[7] 冯侨，邓娟，沈静，等.LTE系统中ZC序列的实现方法[P]：CN 101826890 A.2010.09.08.