摘 要: 提出了一种高效的增量式模糊聚类算法。该算法仅对新增数据计算相似系数而直接聚类,其结果和广泛运用的传递闭包法、最大支撑树法等算法相同。
关键词: 模糊聚类 增量式算法 数据挖掘
聚类分析是数据挖掘和知识发现的重要手段。在聚类分析中,经常存在大量的模糊信息,因此,模糊聚类得到了广泛的研究和应用。经典的模糊聚类算法在获得模糊相似矩阵后,需要进一步的计算才能进行聚类分析。面对新增数据只能将全部数据重新聚类。重新聚类不仅计算量大,而且浪费了前期的计算成果。现代数据库系统一般规模庞大,而且数据增长相当迅速。如果能在前期聚类的基础上,仅对新增数据增量式聚类,则是非常有意义的。为此,本文提出了一种增量式模糊聚类算法。该算法在大大提高聚类分析效率的同时,得到的结果与传递闭包法、最大支撑树法等经典算法相同。
1 模糊聚类算法
经典的模糊聚类算法有传递闭包算法、最大支撑树算法、动态直接聚类算法、基于摄动的模糊聚类算法等,它们都是在模糊相似关系的基础上进行聚类的。建立模糊相似关系的关键是标定各个数据对象之间的相似系数,相似系数反映了数据对象相对于某些属性的相似程度。常用的相似系数计算方法有:数量积法、夹角余弦法、距离法、指数相似系数法、绝对值指数法和绝对值倒数法等。
通过标定相似系数可以得到模糊相似矩阵。模糊相似矩阵一般不满足传递性,只满足自反性和对称性。因此,模糊相似矩阵不是等价关系矩阵,不能直接用于聚类分析。传递闭包法通过求模糊相似矩阵的传递闭包得到数据对象的模糊等价关系,而后对数据对象进行聚类分析。
模糊相似矩阵的收敛性是指:对于n阶模糊相似矩阵R,存在一个最小自然数k(k<n),使得其传递闭包tr(R)=Rk,且对一切大于k的自然数l,恒有Rl=Rk。这表明通过模糊相似矩阵的平方自乘,可以快速求得模糊相似矩阵的传递闭包。在得到传递闭包和给定阈值λ(0≤λ≤1)后,求该闭包的截矩阵就可以得到数据对象的聚类。
最大支撑树法利用了图论中的有关理论,即在求得模糊相似矩阵后,用图来表示模糊相似关系,然后求该图的最大支撑树。在给定阈值?姿后,截断最大支撑树中权值小于λ的边,得到的若干连通子图就构成了λ上的聚类。著名的最大支撑树求解算法有Prim算法和Kruskal算法,它们得到的最大支撑树可能不同,但聚类的结果是一样的。
图1给出的是15个数据的相似系数矩阵。图2表示用Prim算法对前10个数据求得的最大支撑树。给定阈值λ=0.8,截断连接权值小于?姿的边(虚线所示),连通子树形成的聚类用数据的序号表示为:{1,4},{2,3,5,9},{6,7,8,10}。
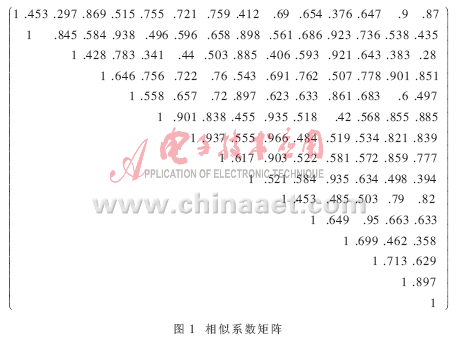
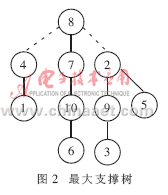
同样,用最大支撑树法对全部15个数据进行聚类,得到的聚类结果为:{1,4,6,7,8,10,14,15},{2,3,5,9,12},{11,13}。
参考文献[7]证明了传递闭包法、最大支撑树法、动态直接聚类法的聚类结果是相同的,它们是互为等价的聚类算法。其他聚类算法的应用也比较广泛,这里不再赘述。
2 增量式模糊聚类算法
在考察新增数据对已有聚类的影响时,如果某聚类中存在同新增数据的相似系数不小于给定的阈值,则称这个聚类为新增数据的贴近类。新增数据对已有聚类的影响至多分三种情况:新增数据不贴近于任何已有的聚类;新增数据贴近已有的某一聚类;新增数据同时贴近多个已有的聚类。确定新增数据属于上述何种情况并对其进行相应的聚类处理,是实现增量式聚类算法的关键。
2.1 算法描述
增量式模糊聚类算法的主要思想是:逐个考察新增数据和已有聚类的贴近程度,如果新增数据和某个已有聚类贴近,则新增数据的贴近类计数器s增1;在已有聚类全部考察完毕后,根据s的值对新增数据归类,或对已有聚类进行调整。下面对增量式模糊聚类算法进行描述。
输入:已有聚类,新增数据。
输出:全部数据的聚类。
算法步骤:
(1)输入阈值?姿和所有新增数据。
(2)对每一个新增数据,令s=0,执行(3)~(5)步。
(3)计算新增数据对已有聚类中数据的相似系数。如果新增数据和这个聚类贴近,则标记这个类贴近,并使贴近类计数器s增1。当前聚类考察结束,考察下一个聚类。
(4)如果对所有聚类都已考察,则转步骤(5),否则转步骤(3)。
(5)聚类。根据s的值,做如下处理:如果s=0,新增数据形成新的聚类;如果s=1,新增数据归入惟一贴近的类,清除类的贴近标记;如果s>1,合并所有贴近的类,将新增数据归入此类,并清除各贴近标记。
在用传递闭包法、最大支撑树法或动态直接聚类法对部分数据进行聚类的基础上,可以使用增量式聚类算法对新增数据进行聚类。为了保证增量式聚类算法和前述算法重新聚类全部数据的结果相同,这些算法中关于相似系数的求法和阈值λ的设定必须保持一致。下面结合最大支撑树的生成过程来说明增量式模糊聚类算法和最大支撑树算法的等价性。
2.2 算法说明
如图3所示,算法中s的三种取值对应初始最大支撑树的调整情况。其中加粗的结点和连线表示初始聚类的最大支撑树,细线表示新增数据贴近最大支撑树结点的可能情形,有“×”标记的边将在树的调整过程中被剪断,实线标记的边权值(相似系数)不小于λ虚线标记的边权值小于λ。
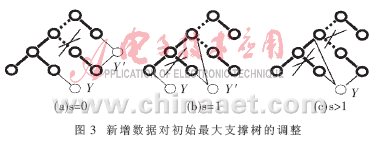
(1)s=0,新增数据同已有聚类都不贴近。调整后的最大支撑树有二种可能的形状:新增结点(图3(a)中的Y)直接连接到某个结点上,或者新增结点(图3(a)中的Y′)连接到多个结点上。由于在基于最大支撑树聚类时,权值小于λ的边都将被截断,所以,已有聚类结果保持不变,而新增数据形成新的聚类。
(2)s=1,新增数据仅贴近一个已有聚类。如果已有聚类只存在一个相似数据,则新增结点(图3(b)中的Y)直接连接到该数据结点;如果已有聚类存在多个相似数据,则剪断初始连通子树中权值较小的边,新增结点(图3(b)中的Y′)后的子树仍是最大支撑子树。无论出现哪种情况,同一子树中的结点调整后仍在同一个子树中。因此,调整只将新增数据归入贴近聚类,而不影响其他的聚类。
(3)s>1,新增数据至少贴近二个已有聚类。当调整产生新的最大支撑树时,新增结点与多个聚类的结点连接。若同一子树内产生了回路,其处理方法和图3(b)中的Y′一样;而子树之间必然产生回路,消除回路时剪断的边的权值必小于?姿,从而使这些子树由权值大于?姿的边连接,合并成了一个如图3(c)所示的新的子树。
综上所述,增量式算法对每个新增数据的归类及对已有聚类的调整,都和重新生成最大支撑树的对应调整情况相同,因此,增量式聚类和最大支撑树法重新聚类的结果是相同的。由于传递闭包法、最大支撑树法、动态直接聚类法是等价的,故增量式聚类算法也和这些算法之间互为等价。
3 实验与分析
在采用最大支撑树法对前10个数据聚类的基础上,采用增量式聚类算法对后面5个数据进行聚类。对第11个新增数据,已有各类中的数据和它相似的系数都小于?姿,故算法中s=0,新增数据单独形成新的聚类,结果如下:
{1,4},{2,3,5,9},{6,7,8,10},{11}
对第12个新增数据,仅第二个聚类存在相似系数不小于?姿的数据,故s=1。新增数据归入第二个聚类中,结果如下:
{1,4},{2,3,5,9,12},{6,7,8,10},{11}
第13个数据和第12个数据的情况相同,也归入已有的聚类:
{1,4},{2,3,5,9,12},{6,7,8,10},{11,13}
对第14个数据,第一个和第三个聚类都存在和它相似的、系数不小于?姿的数据,故s=2,这使得上一步的第一个和第三个聚类合并:
{1,4,6,7,8,10,14},{2,3,5,9,12},{11,13}
第15个数据和第12、13个类似,归入已有的聚类:
{1,4,6,7,8,10,14,15},{2,3,5,9,12},{11,13}
图1中已给出了用最大支撑树法聚类全部15个数据的结果,这一结果和增量式聚类的结果完全相同。在原始聚类结果为空的基础上,用增量式聚类算法对15个数据聚类,所得到的结果也和上面的结果相同。
增量式聚类算法在效率上比最大支撑树算法和传递闭包法有很大提高。假定全部数据量为n,其中已聚类的数据量为m,增量式聚类算法主要耗时在算法的步骤(3)上,最坏情况下每个新增数据都要针对全部已聚类数据计算相似系数,计算量是:m+(m+1)+……+(m+(n-m-1))=(n2-n+m-m2)/2。在无前期聚类结果的情况下(m=0),其计算量是(n2-n)/2,小于最大支撑树算法中Prim算法的3n3/2及Kruskal算法的n3~n3log2n,也小于传递闭包法的n3~n3log2n,与动态直接聚类法的计算量3n2/2处在同一数量级。
4 结 论
本文提出的增量式模糊聚类算法和传递闭包法、最大支撑树法、动态直接聚类法等价,相关实验结果也证实了这个结论。增量式算法只需对已聚类数据计算相似系数,不用计算已聚类数据之间的相似系数,相对其他算法而言,其计算量已大为减小。
在发现海量数据库的知识时,尤其是在数据快速增长的情况下,利用本文所提出的增量式聚类技术,不仅有利于提高聚类分析效率,而且有助于维护和扩充聚类结果,降低知识库维护的开销。
参考文献
1 Zadeh L A.Fuzzy sets.Inf Cont,1965;8(3)
2 Ruspini E H.Numerical methods for fuzzy clustering. Information Sciences,1970;2(3)
3 Dunn J C.A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters. Cybernetics,1974;3(3)
4 Bezdek J C.Cluster validity with fuzzy sets.Cybernetics, 1974;3(3)
5 韩立岩,汪培庄.应用模糊数学.北京:首都经济贸易大学出 版社,1989
6 史忠植.知识发现.北京:清华大学出版社,2002
7 罗承忠.模糊集引论(上册).北京:北京师范大学出版社,1985

