抗混叠Contourlet变换在煤矿图像重构算法中的应用-AET-电子技术应用

抗混叠Contourlet变换在煤矿图像重构算法中的应用

来源：电子技术应用2012年第4期

刘丽虹1，俞啸1，胡延军1,2

1. 中国矿业大学信息与电气工程学院，江苏徐州 221008； 2. 中国矿业大学物联网（感知矿山）研究中心，江苏徐州 221008

摘要： 将抗混叠的Contourlet变换应用到基于压缩感知理论的矿井图像重构算法中。仿真实验表明，在相同的观测系统下采用OMP算法对矿井图像进行重建时，相比于传统的Contourlet变换和Sym4小波变换，基于抗混叠Contourlet变换的压缩感知重构的图像恢复效果更佳。

关键词： 压缩感知抗混叠 Contourlet变换稀疏基重构

中图分类号：
文献标识码： A
文章编号： 0258-7998(2012)04-0110-03

Using non-aliasing Contourlet transform in restructing algorithm of mine images

Liu Lihong1, Yu Xiao1, Hu Yanjun1,2

1. School of Information and Electrical Engineering, CUMT, Xuzhou 221008, China; 2. Internet of Things Perception Mine Research Center, China University of Mining and Technology，CUMT, Xuzhou 221008, China

Abstract： This article applied non-aliasing Contourlet transform to reconstruction algorithm of mine images based on theory of compressed sensing. Simulation indicates that reconstruction result of compressed sensing reconstructed algorithm, based on non-aliasing Contourlet transform, is better than based on traditional contourlet transform and Sym4 wavelet transform, when reconstruct one mine image with OMP algorithm under the same observing system.

Key words : compressed sensing; non-aliasing; Contourlet transform; the basis of sparse; reconstruction

多媒体传感器系统在煤矿井下应用的研究已经引起国内外研究人员的关注，其中能耗问题一直是研究热点，需要对多媒体节点进行合理设计。在降低节点传输负载、节约网络有限能量的同时，完成多媒体信息的压缩编码、冗余信息融合等处理。常用的编码算法在数据采集端按照奈奎斯特采样定理进行数据采集，造成了存储空间及节点能量的浪费。研究如何突破以奈奎斯特采样定理为支撑的信息获取、处理、融合、存储及传输等方式是推动煤矿信息化进一步发展的关键[1]。近年来,由DONOHO D、CANDES E及TAO T等人提出的压缩感知理论为解决这一问题提供了新的思路，该理论以远低于奈奎斯采样频率对稀疏或可稀疏信号进行采样，仍可以精确恢复出原信号，具有编码简单、解码复杂的特点。这样在煤矿井下可以铺设性能较弱的多媒体传感器节点，不仅节约成本，也降低了采集端的工作负荷。将复杂的解码过程交由井上计算能力强大的服务器处理，为井上调度室的指挥控制提供清晰的井下现场图像。故该理论在煤矿井下无线多媒体传感器网络(WMSN)中具有很大的应用前景,如图1所示。

    压缩感知理论中，随机采样不需要先验知识，只需寻求更好的正交稀疏变换，得到变换域中更稀疏的信号，便可提高压缩感知和信号重构的性能。压缩感知恢复算法中常用的正交变化有DCT[2]、傅里叶变换[3]、小波变换[4]等，信号经过变化后越稀疏，越有利于提高压缩感知信号重构的性能。近年兴起的以Contourlet变换为代表的多尺度几何变换具有良好的稀疏性质，经其变换得到的稀疏系数要比小波系数更稀疏，更有利于信号的重构。但是其基函数在频域中是非局部的，造成了频率混叠现象，需要用理论上更多的系数来表示,而抗混叠Contourlet[5]变换恰可以解决这个问题。
   本文将双通道滤波器组与方向滤波器组相结合，实现了一种抗混叠的轮廓波变换,提出基于抗混叠Contourlet变换的矿井图像压缩感知重构方法。

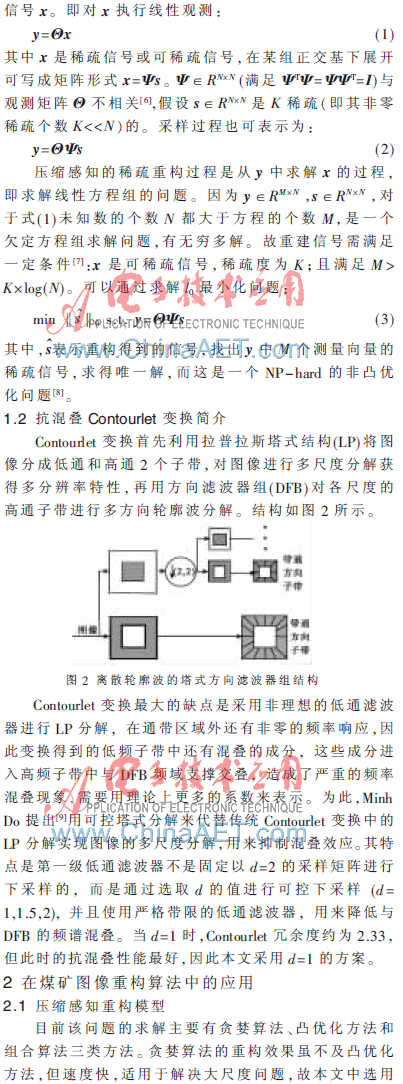
从图中可以看出抗混叠Contourlet的效果要略好于传统的Contourlet变换。当采样率小于0.3时，恢复的图像失真严重，比较它们的PSNR值已经没有意义。采样率高于0.3时，在同等采样率，恢复算法都采用OMP重构算法的情况下,基于Contourlet变换和抗混叠Contourlet变换的重构图像的质量要比基于Sym4小波的更优，因为Contourlet变换比小波变换更能稀疏地表示矿井图像中的边缘和轮廓信息。抗混叠Contourlet变换抑制了混叠效应，其基函数的频域局部性更好，具有更集中的方向选择性, 验证了图像抗混叠Contourlet变换的稀疏性更好。
本文将抗混叠 Contourlet 变换应用于矿井图像的压缩感知重建中。OMP重构算法是目前图像重建的一种比较经典的算法,在此优化算法下,将抗混叠Contourlet变换、传统Contourlet变换和Sym4小波变换作为压缩感知稀疏域，并观察其表现。仿真结果显示，相较于小波变换和Contourlet变换，抗混叠Contourlet变换不管在恢复的视觉效果还是PSNR指标上,都比Sym4小波和传统 Contourlet变换更好。目前多尺度几何分析作为图像处理的一个研究热点，压缩感知作为一种新技术，其理论框架和算法实现都还在发展中, 并能够解决煤矿井下的实际问题，有望给信号处理领域带来重大影响。
参考文献
[1] 曹新德.压缩感知理论在井下救灾系统中的应用研究[EB/OL](2010-12-28).中国科技论文线,http://www.paper.edu.cn/index.php/default/releasepaper/content/201012-1175.
[2] 沙威.压缩感知引论[EB/OL](2008-11-20). http://www.eee.hku.hk/~wsha.
[3] 岑翼刚.基于单层小波变换的压缩感知图像处理[J]. 通信学报,2010,31(8A):53-55.
[4] LUSTIG M, DONOHO D, PAULY M. Sparse MRI: the application of compressed sensing for rapid[J]. Magnetic Resonance in Medicine 2007,58:1182-1195.
[5] CANDES E J, DEMANET D L, YING L. Fast discrete curvelet transforms[EB/OL]. http://authors.library.caltech. edu/6810/.2009-11-29.
[6] BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007,24(4):118-121.
[7] DONOHO D. Compressed sensing[J]. IEEE Transactions on Information Theory，2006,52(4):1289-1306.
[8] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory,2006.52(4):1289-1306.
[9] LU Y, DO M N. A new contourlet transform with sharp frequency localization[C]. IEEE International Conference on Image Processing, 2006(10):1629-1632.
[10] 赵瑞珍.压缩传感与稀疏重构的理论及应用[EB/OL](2009-10-30).中国科技论文在线，http://www.paper.edu.cn/index.php/default/releasepaper/content/200910-662.
[11] DONOHO D, TSAIG Y. Extensions of compressed sensing[J]. Signal Processing, 2006,86(3):533-548.
[12] TROPP J, GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans. Inform, Theory,2008,53(12):4655-4666.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容