摘 要: 结合三维地震层位数据,使用OpenGL图形库和NURBS模型,分析了NURBS 构造自由曲面的方法。讨论和总结了相关关键算法和技术,实现了地震层位的三维多方显示,为很多领域的空间数据曲面拟合提供了通用性方法。
关键词: NURBS OpenGL 地震层位 可视化
地震数据和测量数据能否被正确解释是准确定位矿藏位置的关键,只有对上述原始测量数据做大量处理之后才能获得正确地层结构信息[1]。近年来,三维可视化技术被成功应用到地质勘探领域中,它可对各种复杂的地质模型和三维地震数据进行描述,并以直观的形式在三维空间显示。通过三维空间对地震数据的可视化显示,使油气勘探工作者能更加深刻和准确地理解地质构造以及各种地质现象的发生、发展和影响,从而提高钻井的准确率和成功率。
地震层位的三维显示是地质勘探可视化的基本功能之一。它把经过速度场解释后的层位信息在三维空间中实现多方显示。本文研究了地震层位的NURBS曲面拟合方法,并在Sun Blade 2000工作站Solaris平台下,基于NURBS使用OpenGL,在X/Motif环境下实现了地震层位模型的建立和显示。
1 地震层位模型的表达
地层面又称层面,是地层与地层的分界面,也是通过地震剖面来识别层序的关键界面之一。在一个油气探区内,经过处理获得的地震层位信息可能由若干层组成。一般情况下,各地层在地下由浅到深排列,每个特定层位可以由一个空间曲面来拟合。但在复杂地质情况下由于断层的错断切割,一个层位可能由若干个空间曲面组成,但这些空间曲面一般是相互独立的[2]。因此,地震层位的表达问题就可以转换成多个空间曲面的表达问题。
地震层位信息是一个离散的四维数据集{x,y,z,p},其中x、y、z描述了空间某点的坐标信息,p是该点的物性,一般可以用颜色等来标注。关键问题是如何通过插值的方法,描述这些空间离散数据点集,从而还原地质层面或者断面的空间形态,并最终多方位显示给用户。下面就以一个层位数据集中的空间曲面为对象,以该曲面的数据集为基础,用一个计算机能生成的曲面来插值这些数据点。通过对多个独立的曲面进行这样的处理,来模拟地层和断层的形态、空间位置和相互关系。
2 地震层位模型的NURBS曲面建立
NURBS 方法是最广为流行的自由曲线和自由曲面描述技术。应用NURBS方法可统一表示初等解析形状和自由型曲线曲面、有理非有理Bezier曲线曲面和非有理B样条曲线曲面[4]。本文采用NURBS对地震层位的单个独立曲面进行拟合,由多个曲面的组合来表达复杂的层面和断面。
2.1 NURBS的定义
K次NURBS曲线的数学表达式如下:
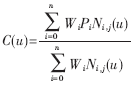
式中Pi是特征多边形顶点位置矢量,Wi是相应控制点的权因子,分别与控制顶点Pi相联系,节点向量中节点个数m=n+k+1,n为控制点数,k为B样条基函数的次数,Ni,j(u)是k次B样条基函数,其递推公式如下:
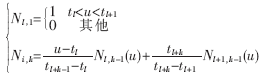
NURBS曲面是曲线的推广,由双参数变量分段有理多项式定义的NURBS曲面如下式:

2.2 NURBS曲面拟合地震层位的步骤和关键算法
2.2.1 地震层位数据预处理
找一个曲面使之通过已知数据点,实际上就是已知型值点求相应样条曲面的控制点,即控制点的反算问题。由于反算曲面要求型值点为矩形网格数据,而实际层位数据常常在XOY投影平面内并不呈矩形分布,因此要对层位数据进行重采样,使之最终在形式(数目)上表现为矩形,常用如下3种方法:
(1)如果原始数据较为密集,可以重新采样,摒弃一些多余数据,使之成为矩形网格分布。
(2)对于各行上点数目不相等的情况,可以在点少的行上使用最末网格点重复法。
(3)对于点数目较多的行,以最短的行的点数为基准,隔点采样,构造不等间距网格。
2.2.2 反算B样条曲面控制点
本文使用NURBS的退化形式——双三次B样条曲面来拟合地震层位的方法,可以满足精度要求。反算控制点有双向曲线反算法、广义矩阵法等方法[4]。本文采用双向曲线反算法,即对n×m的型值点矩阵P,先横向使用B样条曲线的边界条件及反算公式,求出n×(m+2)的n组样条曲线控制点矩阵M;再把M的每列看成曲线上的型值点,以相同的方法纵向反算控制点,得到(n+2)×(m+2)的曲面控制点矩阵Q。对于B样条曲线,控制点Q和型值点P应满足:

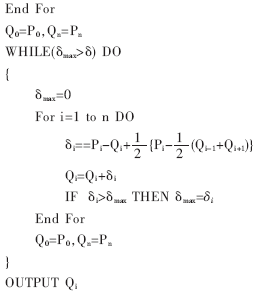
2.2.3 确定节点矢量

3 震层面的OpenGL绘制
确定了控制点和节点矢量后就可以使用OpenGL来生成NURBS曲面了。OpenGL是目前跨平台最广泛的三维图形引擎,也是目前应用最广泛的事实上的三维图形工业标准。它具有的GLU库提供了NURBS曲线和曲面接口。绘制NURBS曲面的基本步骤如下[3]:
(1)调用gluNewNurbsRenderer( )创建NURBS对象指针,在绘制曲面时使用该指针。
(2)调用gluNurbsProperty( )控制NURBS对象的采样方式及显示模式等属性。
(3)调用gluBeginSurface( )开始绘制曲面。
(4)调用gluNurbsSurface( )创建并绘制曲面。
(5)调用gluEndSurface( )结束绘制曲面。
由于直接关系到对NURBS的正确理解和曲面能否生成,因此,下面重点说明函数gluNurbsSurface(GLUnurbs *nurb,Glint sKnotCount,Glfloat*sKnots,GLint tKnotCount,Glfloat*tKnots,GLint sStride,GLint tStride,Glfloat*control,GLint sOrder,GLint sOrder,GLint tOrder,Glenum type)的各个参数和用法。其中sKnots和tKnots分别为曲面在u和v方向的节点序列,程序中一般要规约处理到区间[0,1]内,节点的取法上文已详细讨论。sKnotCount和tKnotCount为这二个方向的节点数目,而sOrder 和tOrder为这二个方向上的多项式基函数的阶数。本文采用双4阶的NURBS曲面。变量sStride和tStride表示每个参数方向上控制点之间浮点数的个数。变量control指定控制点数组。由于NURBS中节点、控制点、阶数间在u、v方向上必须分别满足m=n+k+1,其中m、n、k+1分别为该方向上节点个数、控制点个数、阶数,所以control数组中必须有(sKnotCount-sOrder)×(tKnotCount-tOrder)个控制点。
提供了控制点及节点数据后就可以调用函数gluNurbsSurface生成NURBS曲面来拟合地震层位。利用OpenGL的强大功能和友好接口,可以很方便地加上材质、光照和纹理效果,并且通过平移、旋转来实现多方显示。本文采用胜利油田实际地震采样数据,拟合后,某地层单个层位的点云方式和NURBS曲面方式的实现分别如图1和图2所示。多个地层的点云方式和NURBS曲面方式的实现分别如图3和图4所示。由图可见,NURBS对连续层位的形态描述取得了很好的拟合效果。


4 结束语
本文基于NURBS模型,分析了NURBS构造地震层面的方法,讨论和总结了相关关键算法,使用OpenGL实现了地震层位的三维多方显示。OpenGL是性能优秀的图形接口,具有稳定、可靠、易用、易扩展和扩充等优点,是进行三维可视化开发的的首选底层引擎。NURBS方法是建立在非有理Bezier方法和非有理B样条方法基础上,为自由型曲面的精确表示提供了公共的数学表达式。该方法具有计算稳定、速度快,且在比例、旋转、平移和投影等图形变换下具有不变性。所以基于NURBS使用OpenGL拟合地震层位具有建模快、算法清晰、程序稳定的特点。相对于其他建模方法而言,更利于实现。但对于更复杂的模型,如被多个断层作用的地震层位,模型表达和实现都将有一定难度。这时,结合其他优秀建模方法,如三角网格法(Delaunay三角剖分)是一个行之有效的思路。这也将是下一步需要继续做的工作。
参考文献
1 石教英,蔡立文.科学计算可视化算法与系统.北京:科学出版社,1996
2 张剑秋,张福炎.地震层位信息三维可视化方法.石油地球物理勘探,1998;33(1)
3 李颖,薛海斌,朱伯立.OpenGL技术应用实例精粹.北京:国防工业出版社,2001
4 孙家广,杨长贵.计算机图形学.北京:清华大学出版社,1995
5 卓磊.地震勘探三维可视化方法研究与实现.中国科学院地质与地球物理研究所硕士学位论文,2002
6 施法中.计算机辅助几何设计与非均匀有理B样条.北京:高等教育出版社,2001

