摘 要： 提出了一种基于Contourlet变换的图像内容认证算法。介绍了Contourlet变换并分析了其特点， 详细描述了水印的嵌入与提取过程，采用形态学算子提高了检测率。仿真实验表明,本算法在保证水印的不可见性的前提下，对常见的非恶意操作鲁棒而对恶意操作脆弱。
关键词： Contourlet变换； 图像认证

    近几年来,随着网络技术的发展，图像的内容认证也不断发展起来。由于多媒体内容容易被修改，在内容受到怀疑时，一个能可靠验证篡改是否发生的真伪鉴别系统就显得非常重要。采用数字水印技术可以实现图像的内容认证。
    图像内容认证技术分为基于脆弱水印的精确认证技术和基于半脆弱水印的选择认证技术两大类。轻微的信号处理操作（如高品质的JPEG压缩）在许多场合常被认为是可接受的操作，因此选择性认证更适合于实际应用的需要。半脆弱水印提供了一种实现选择性认证的方法。它是一种对正常图像处理鲁棒而对恶意篡改脆弱的水印。篡改发生时，半脆弱水印认证系统不仅可以提供篡改的破坏量及篡改位置，而且可以分析篡改类型。在实际应用中，为了描述选择性认证系统，将失真分为合理失真和不合理失真两组。当作品失真为合理失真时，认证系统应该能让作品通过认证；相反，作品则不能通过认证[1-2]。
    过去的十几年里，研究者们提出了许多用于图像内容认证的半脆弱水印算法，这些算法大致可以分为空域算法和变换域算法。由于空域算法对非恶意操作的鲁棒性较差，因此变换域的算法更符合实际应用的需求。1999年FRIDRICH提出了一种基于DCT的分块自嵌入脆弱水印算法，该算法将图像分为互不相交的8×8图像块，对其高7位的DCT系数按一定的码长量化编码后，采用固定“偏移值”嵌入另一图像块的最低位，从而在定位被篡改图像块的同时，还可以利用水印信息近似恢复被篡改图像块的内容。一种典型的DCT域的半脆弱水印算法是由LIN和CHANG提出的，该算法不仅能够检测和定位篡改区域，还能够较好地抵抗JPEG压缩操作(QF=50)。近年来，基于Contourlet的图像水印算法受到重视[3-5]，这些算法大都将水印嵌入到能量较大的Contourlet变换方向子带中，较好地利用了方向子带的纹理特性。
    本文提出了一种基于Contourlet变换的半脆弱水印算法。该算法不分块，避免了块效应和基于分块独立性产生的量化攻击,能够与现有的压缩标准(如JPEG、JPEG 2000)结合起来，能较好地检测出发生的篡改并定位。
1 Contourlet变换及特性
1.1 Contourlet变换
    Contourlet变换是利用拉普拉斯塔形分解LP(Laplacian Pyamid)和方向滤波器组实现的一种多分辨的、局域的、多方向的图像表示方法[6-7],因此也可以称作金字塔型方向滤波器组PDFB(Pyramidal Directional Filter Bank)。PDFB的过程为：首先对图像进行LP变换和多尺度分析，以捕获奇异点；然后由方向滤波器组DFB将分布在同方向上的奇异点合成一个系数，这种结构使得Contourlet变换具有较优的非线性逼近性能。这一过程在粗糙图像上重复进行，从而将图像分解为多尺度方向子带。图1为利用Contourlet变换对图像进行分解的过程示意图。

1.2 Contourlet变换特性
    Contourlet变换是一种基于图像的几何性变换，具有以下特点：
     (1)对图像进行更加灵活的多尺度描述。Contourlet变换的方向子带更具体地体现了该方向上的轮廓和边缘分布。同时在Contourlet变换子带中，方向子带中的奇异点也代表了图像的重要特征系数。利用Contourlet变换，既可以提取出图像方向上的纹理特性，又可以提取出图像的重要系数。水印嵌入到这样的方向子带中，能很好地协调鲁棒性与透明性之间的矛盾。
    (2)系数的概率分布特性：在零均值上方有尖锐的峰起，同时在峰起的两侧迅速衰减。这样，Contourlet变换后的方向子带系数边缘概率分布可以用广义高斯模型拟合。假定嵌入的水印信息W(x,y)由一个服从于均值为0、方差为1的高斯分布的伪随机实数序列组成,把这样的一个水印嵌入到Contourlet变换方向子带的过程，可以看成是两个服从于同分布的信号的叠加。这样不仅满足视觉上的不可见性，而且在数理统计上也是隐蔽的。
    (3)由于LP的冗余性，Contourlet变换具有4/3的冗余度[8]。对于水印而言，冗余度意味着有更多的可嵌入空间。
2 算法分析
2.1 数字水印嵌入算法
    水印嵌入时对原始图像进行Contourlet变换,在其低频子带嵌入水印。具体过程如下：
    (1)为了增强水印图像的安全性，对二值水印图像采用Arnold置乱变换进行置乱，将置乱次数作为密钥保存。
    (2)采用Contourlet变换对原始灰度图像进行2级拉普拉斯金字塔变换和最精细子带8方向分解，提取其低频逼近子图cA1，且满足cA1的大小与水印大小相同。
    (3)为了实现奇偶量化地嵌入水印，需要计算量化参数:
  
    (4)改变Contourlet变换后的低频子带系数，完成水印信息嵌入。当水印比特为1时，a(i,j)=(round(a(i,j)÷q)+1)×q；当水印比特为0时,a(i,j)=(round(a(i,j)÷q)-1)×q。
    (5)进行Contourlet逆变换，得到含水印信息的图像。
2.2 水印提取及认证算法
    水印的提取过程不需要原始图像，具体过程如下：
    (1)对含水印信息的图像进行与水印嵌入阶段相同
的Contourlet变换。(2)从低频子带中提取水印，若mod(round(a(i,j)÷q),2)=1,则w′(i,j)=1；否则，w′(i,j)=0。遍历低频子带所有系数，得到未反置乱的水印w′。(3)利用置乱密钥对w′进行反置乱，最后提取二值水印图像。
    将提取水印比特与原始水印比特进行比较即可得到水印差图，它可被用于图像篡改区域的定位。具体认证过程为：首先判断归一化相关系数(NC)值，若NC≥T（T为判定阈值），就认为含水印图像通过认证，否则认为含水印图像遭受了恶意攻击;然后根据水印差图获知发生错误的水印比特，并在定位图的相应位置用灰度值255表示。通过白点的多少和位置可以判断图像被篡改的程度和位置。
    为了提高检测率，采用了形态学算子。根据观察，大多数由非恶意操作引起的虚警误差的分布都是孤立的，而形态学算子作为信号处理中的一个非线性技术可以去除非恶意操作引起的孤立虚检点，使得篡改区域更加紧凑，以此降低虚警率。腐蚀和膨胀是两个最基本的形态学算子，这两个算子又常常被联合起来成为开运算和闭运算。本算法首先使用了开运算，接着使用了闭运算。实验结果证明，形态学算子的使用提高了算法的检测率。
3 仿真实验
    为了评价水印算法的性能,本文采用大小为256×256、位深为8 bit/pixel的Lena灰度图像进行各种测试。在Matlab仿真实验中，Contourlet变换的LP采用“9-7”金字塔滤波器,Contourlet变换的DFB采用“pkva”方向性滤波器。对输入图像Lena进行2级LP分解，得到1个近似图像I2和2个带通子图像B1、B2，其中B1为最精细子带图像，B2为次精细子带图像。然后分别对B1、B2进行8方向分解和4方向分解。
3.1 不可见性测试
     对原始图像嵌入水印并提取水印，结果如图2所示。对水印可见性的评估可以用定量度量方法和主观测试方法。本文对于图像视觉质量的定量描述使用峰值信噪比（PSNR）。通过实验提取的水印的NC为1.00，含水印图像的PSNR为33.005，说明嵌入的水印对于HVS具有较好的不可见性。
3.2 非恶意操作的鲁棒性测试
    对含水印的Lena图进行各种非恶意的操作，提取的水印如图3所示。

3.3 恶意操作的脆弱性测试
      对含水印的Lena图在左上角裁剪原图的1/16(6.25%)，提取的水印如图4(a)所示，定位效果如图4(b)和图4(c)所示；在左上角裁剪原图的1/4(25%)，提取的水印如图5(a)所示，定位效果如图5(b)和图5(c)所示。
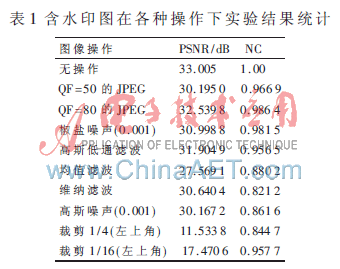
     统计含水印图像在各种操作的NC和PSNR，结果如表1所示。

    本文提出了一种基于Contourlet变换的图像内容认证算法。实验结果表明，本算法在水印嵌入位置的选择和嵌入策略上很好地协调了嵌入水印图像的不可见性和鲁棒性，并能较精确地检测和定位篡改。篡改发生后，如何高质量地恢复图像内容有待进一步研究。
参考文献
[1] COX I J, MILLER M L, BLOOM J A. 数字水印[M]. 王颖，黄志蓓,等，译.北京：电子工业出版社，2003.
[2] 吴金海，林福宗．基于数字水印的图像认证技术[J]．计算机学报，2004，29(9):1153-1161.
[3] 李海峰,宋巍巍,王树勋.基于Contourlet变换的稳健性图像水印算法[J].通信学报,2006,27(4):87-94.
[4] JAYALAKSHMI M, MERCHANT S N, DESAI U B.Digital water-marking in Contourlet domain[C].The 18th International Conference on Pattern Recognition，2006(3):861-864.
[5] BOUZIDI A, BAAZIZ N. Contourlet domain feature extraction for image content authentication[C]. Proceedings of the  2006 International Conference on Intelligent Information Hiding and Multimedia Signal Processing, 2006:202-206.
[6] DO M N,VETTERLI M. The Contourlet transform: an efficient directional multiresolution image representation. IEEE  Transactions on Image Processing,2005, 14(12):2091-2106.
[7] DO M N, VETTERLI M. Contourlets: a new directional  multiresolution image representation[J].Signals，Systems and Computers,2002(1):497-501.
[8] 焦李成,孙强.多尺度变换域图像的感知与识别:进展和展望[J].计算机学报,2006,29(2):177-193.