摘 要: FCM算法作为基于目标函数的模糊聚类算法中最经典的算法之一,在实际应用中得到了深入的研究,但FCM算法需要人为给定分类数C,因此破坏了聚类的无监督性。针对FCM算法的不足,提出了利用密度指标确定初始聚类数目上限Cmax,并且对有效性指标进行了改进,计算对于(1,Cmax]中的每一个c对应的有效性函数值,根据有效性评判,确定最佳聚类数,实现了自动得到最佳分类数的算法。
关键词: 模糊C-均值;模糊聚类;密度函数;有效性指标
模糊C-均值(FCM)聚类算法是聚类分析中最重要的聚类算法之一,在特征分析、模式识别、图像处理、分类器设计等技术中应用非常广泛[1]。
但FCM算法存在着以下几点不足[1]:(1)算法的性能依赖于初始聚类中心和初始隶属度函数的选取;(2)事先必须确定聚类的个数;(3)模糊指标的选择;(4)收敛到局部极值问题。
很多学者针对这些问题进行了研究。如参考文献[2]采用贪心算法选取有代表性的点作为初始中心,提出一种基于权重的初始中心点选取算法, 得出了优化聚类初始中心的模糊C-均值方法;参考文献[5]通过加入点密度加权系数和特征矢量权重, 提出一种具有两阶段的模糊FCM聚类改进算法。
本文针对FCM算法事先必须确定聚类个数这一不足,提出了两点改进思路: (1)在初始聚类中心的选择上提出了一种密度指标方法,利用该方法可以在全局范围内选取初始值,降低了算法受初始值影响易陷入局部最优的可能性,从而得到最大聚类个数;(2)提出了有效性指标的改进算法,从而更加客观公正地评判聚类结果有效性。
1 聚类数c和初始聚类中心的确定
1.1 密度指标
密度指标的方法对聚类中心的选择有重要意义,该方法的基本规则是,保证成为聚类中心的数据点周围的数据点密度大于事先设定的临界值。它从全局出发,对每个数据点平等相待,认为每个数据点都有可能成为聚类中心,并根据每个数据点周边的数据密度计算该数据点是否有可能成为聚类中心,甚至计算成为聚类中心的可能性的大小。这样,可以保证各个聚类中心点周边数据点密度最高,使得算法不会因为初始值影响而陷入局部最优。



2 自适应最佳FCM聚类个数确定算法
在确定最佳聚类数时,需要对从1~n的所有c值进行循环运算,而每一个c值在运算过程中都会产生聚类中心,这样聚类中心的数量就会随着样本数目的增加而急剧增加,致使算法的时空复杂度很大。本论文将利用密度指标确定初始聚类数目上限Cmax,确定初始聚类数目上限后,就可以减少循环运行次数,从而相应地减少初始化聚类中心的数目,大大提升算法的时空效率。
因为聚类过程没有预先定义数据集中哪一种期望的关系是有效的,所以它是一种无监督的学习方法,因此很多聚类算法依靠假设和猜测进行有效性的判断,为解决此问题,多数学者提出了聚类有效性指标方法,它被认为是评判聚类结果有效性的一种客观公正的质量评价方法。本论文将利用改进的有效性指标计算对于(1,Cmax]中的每一个c对应的有效性函数值,根据有效性评判,得到最佳聚类数Copt。
算法的描述如下:
输入:待聚类分析的数据集合Dset.txt,最大迭代次数Rmax。
输出:最佳聚类数Copt、迭代次数l和目标函数值obj。
算法:

3 实验分析
实验数据:IRIS数据;
数据特征:分为三种类型,每种类型中包括50个四维的向量。
实验步骤:
(1)先按照传统FCM算法对数据集聚类,此时需预先给出聚类数c为3,并在集合中随机选出3个初始中心,得到算法目标函数的变化曲线如图1所示。
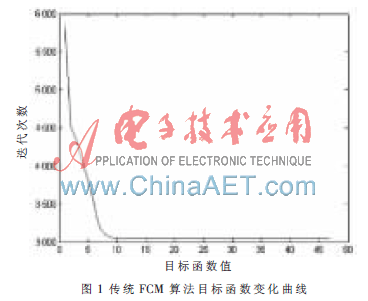
(2)根据密度指标函数Dsty(data),得出初始聚类数目Cmax=8,并根据Ics( )得到8个初始聚类中心。
(3)根据有效性指标和类合并的方法步骤,给出相似度计算条件?着1=0.4,?着2=0.8,经过循环计算得到最终的聚类结果,Copt=3,目标函数变化曲线如图2。
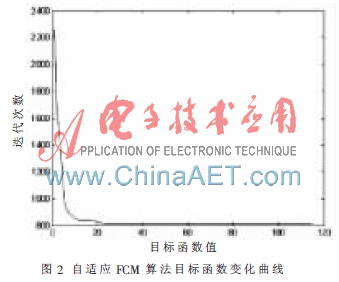
通过实验可以看出改进后的FCM 算法根据密度指标函数自适应地得到最大聚类数Cmax和聚类中心,再根据有效性指标和类的合并方法得到最优的聚类数Copt和聚类中心,而后用 FCM 算法计算得到的结果属于有效聚类,能更准确地对数据集进行划分,且通过对比目标函数的变化曲线,可以看出改进后的算法由于是在全局范围内选择初始值,目标函数相对于传统FCM算法更容易收敛到全局最优,降低了算法对初始中心的依赖。因此本论文提出的自适应模糊C-均值算法是有效的。
由于实验中选取的数据集属于特定类型的数据,按照改进后的算法得到的结果更合理也更准确,尚未观察出聚类结果存在的不合理性,但是当数据集合不是IRIS类型的数据时,很可能得不到理想的聚类效果,本论文尚未对所有类型的数据集做实验分析,这将是今后进一步研究的方向。
参考文献
[1] 江克勤,施培蓓.优化初始中心的模糊C-均值(FCM)算法[J].合肥工业大学学报(自然科学版),2009,32(5):762-
765.
[2] 单凯晶,肖怀铁.初始聚类中心优化选取的核C-均值聚类算法[J].计算机仿真,2009,26(7):118-121.
[3] 齐淼,张化祥.改进的模糊C-均值聚类算法研究[J].计算机工程与应用,2009,45(20):133-135.
[4] 张国锁,周创明,雷英杰.改进FCM聚类算法及其在入侵检测中的应用[J].计算机应用,2009,29(5):1336-1338.
[5] 刘坤朋,罗可.改进的模糊C均值聚类算法[J].计算机工程与应用,2009,45(21):97-99.

