关键词: 智能混合系统 自然智能 神经网络 专家系统 模糊逻辑
人工智能的核心任务是模拟自然智能。而自然智能表现在不同的层次和不同的方面,因此仿智的方法有多种,如模拟抽象思维层次的符号主义,模拟形象思维层次的联接主义,模拟智能行为层次的行为主义等。虽然各种智能信息处理方法与概念都已提出,并取得不少成果,但相关的研究工作还处在较低的水平,在单独模拟人类智能活动时,尚存在各种局限性。生物物理、心理认知学的研究表明,智能信息处理能力是包括上述各种智能处理能力的综合集成。可以相信,今后智能本质和智能综合集成方面的系统研究将是非常重要的研究领域。
尽管自然智能覆盖面广,但人是万物之灵,应将对人的智能的研究作为重点,并辅以对其他自然智能的研究,从而最终解开智能的奥秘。同时,在研究智能综合集成方面,由于抽象思维和形象思维是人类最主要的二种思维形式,并且符号主义和联接主义学派的方法和理论较为充实,因此,应重点进行上述二者的集成研究,然后将其原理和方法推广到其他广义人工智能的综合集成中。
1 四类典型的智能混合系统
智能混合系统主要涉及专家系统(Expert System,ES)、神经网络(Artificial Neural Network,ANN)和模糊逻辑(Fuzzy Logic,FL)三种技术。神经网络易于表达感性知识,专家系统易于表达理性知识,而理性知识中又含有大量的模糊知识,因此需要使用模糊逻辑来描述。于是,不同技术的组合,便构成了不同类型的智能混合系统,主要有四种(如图1所示)。
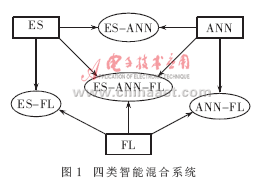
1.1 神经网络与专家系统结合
神经网络与专家系统主要有三种结合方式,下面分别予以介绍。
(1)基于神经网络的专家系统
这类系统又称联接专家系统,其全部或部分功能由神经网络实现,实现方式有两种。
①从神经网络中抽取规则构造专家系统
这种方式希望将神经网络的隐式“黑箱”知识表示为显式规则形式,并用于推理或解释神经网络的行为。在训练前不需要了解领域知识的结构,也不需要将领域知识的结构强加于神经网络,关键是通过神经网络的自组织、自学习来获得易于人类认识、理解的领域知识。
②规则知识编码于神经网络系统
这种方式比较简单,实质是利用神经网络将己有的领域知识进行优化求精,所训练的神经网络在形式上直接对应于专家系统的推理网络,可以直接用于推理和解释神经网络的结论和行为。
上述两种方法的区别在于:前者在对神经网络进行训练之前无需将领域知识的结构强加于神经网络,所学得的神经网络难以进行自我解释,神经网络中的知识只有抽取出来并表示为规则知识后才成为易于理解的显式知识;后者在对神经网络进行训练之前需要将领域知识的结构编码于神经网络中,所学得的神经网络己将知识进行了显式表示,因而具有自我解释能力。
很多学者进行了这方面的研究和开发工作。Gallant[1]首次提出并建立了联接专家系统,Caudill[2]提出了建立额外的小型规则系统用于解释神经网络行为的方法等。
这类混合系统优势在于自学习和自适应能力,可以有效克服专家系统在知识获取方面所遇到的困难,开发时间较短;缺点在于对神经网络拓扑结构、非线性活动函数及各种参数的选择缺乏系统的指导原则,应用领域较窄,其解释能力方面也有待进一步研究。
(2)基于知识的神经网络系统
这类系统也称为专家网络,是由专家系统作为神经模块构成的事件驱动网络。在该系统中,神经元包括“与”、“或”、“非”等逻辑神经元和前提、结论神经元,它们之间的联接权代表专家系统中的确定性因子,故可将专家系统规则集表达为专家网络。
这方面的研究成果主要有:Kuncicky[3]提出的专家网络,Towell[4]提出的一种基于知识的人工神经网络。可以看出,专家网络的缺点是学习时只改变权值,而不能改变网络的拓扑结构,因而不能向不完全的初始规则集增加新的符号规则。为了使专家系统具备学习能力,以期根本解决知识获取的瓶颈问题,对专家系统进行合理描述并且开发有效的学习算法将是十分重要的研究方向。
(3)基于神经网络与专家系统的混合系统
这类系统的基本出发点是将复杂系统分解成各种功能子系统,分别由神经网络或专家系统实现,研究的主要问题包括混合专家系统的结构框架和选择实现功能子系统方式的准则两方面的问题。这两个问题的研究相辅相成,不可分割。混合方式有两种:①从应用的角度出发,对易于获取其产生式规则的子系统使用专家系统技术,其余的功能由神经网络来实现,此时系统的结构由实际问题来决定。②从功能的角度出发,可以用神经网络实现专家系统的规则推理、知识获取等功能,专家系统则负责知识的显式表示和神经网络结论的验证和解释工作。
基于此,Suddarth[5]提出将复杂系统分解为功能子系统的混合系统结构,Tirri[6]则另辟蹊径,用神经网络实现专家系统规则集前提条件。
虽然神经网络与专家系统结合兼有二者之长,但同时也带来了单一技术不曾遇到的问题:①神经网络与专家系统的信息交互问题;②学习过程所引发的系统可信度问题。前者的解决依赖于神经网络与专家系统知识表示的转换机制或同时适合两者的公共知识表示体系,后者的解决有赖于不同体制下的知识的公共表示和统一的参数学习机制。显然,解决上述两个问题己成为实现神经网络与专家系统相结合的当务之急。
1.2 模糊神经网络
模糊神经网络(Fuzzy Neural Network,FNN)是模糊理论同神经网络相结合的产物。它汇集了神经网络与模糊理论的优点,集学习、联想、识别、自适应及模糊信息处理于一体。近年来,FNN的理论及应用得到了飞速发展,各种新的FNN模型的提出以及与其相适应的学习算法的研究不仅加速了 FNN理论的完善,而且它们在实际中得到了非常广泛的应用。本文以此为基础,进一步讨论完整意义上的FNN的网络模型、学习算法、模糊函数逼近性能和学习能力等关键问题,并对今后的研究提出自己的看法。
(1)FNN模型和算法
目前FNN模型绝大多数都是多层前向网络结构,主要区别在于隶属度函数、模糊加权算子、模糊激励函数和输入输出的形式,以及结构与参数的设定和调整方法。
FNN可以分为单纯型和混合型两种:①单纯型FNN:输入输出和连接权全部或部分采用模糊实数,计算结点输出的权相加采用模糊算术算子,函数计算采用扩展原理;②混合型FNN:输入输出和连接权全部或部分采用模糊实数,计算结点输出的权相加还采用了除模糊算术算子以外的模糊逻辑算子,函数计算采用扩展原理。这两种模型既可以处理模糊信息,也可以处理非模糊信息,因为普通实数可以作为一种特殊的模糊数。
这方面成果很多,重要的有:Chen[7]针对基于模糊训练样本的模式分类问题提出了多类FNN分类器,模糊自适应谐振理论(ART)[8]成功解决了模糊信息的存储和记忆问题。除此之外,还有不少文献也都提出了各种各样的FNN模型和算法,不再赘述。
(2)FNN的函数逼近问题
已经证明普通多层前向NN和模糊系统(输入输出均为非模糊数)是连续函数逼近器,并且系统之间可以等价互换,这为在输入输出非模糊的环境下设计模糊神经网络混合系统提供了扎实的理论基础。虽然模糊神经网络系统逼近问题取得了许多理论成果,但是己有结果仅仅是针对采用单值模糊产生器的模糊系统得到的,对于输入输出均为模糊数的FNN函数逼近问题的研究相对比较薄弱,而在设计FNN的同时论证设计模型的逼近性能有时非常必要。因此,FNN函数逼近问题的研究重点是:①寻找能够作为连续模糊函数逼近器的FNN;②给出通用的作为连续模糊函数逼近器的FNN的构造型定理。
在这方面Buckley[9]做了开创性的工作,定义了模糊函数、连续模糊函数和连续模糊函数逼近器等概念,并且证明如果FNN模型是单纯型,则它不可能是一个连续模糊函数逼近器;如果FNN模型是混合型,则它可能是一个连续模糊函数逼近器。但是,这不是一个构造型定理,它没有给出设计连续模糊函数逼近器的FNN的方法。Feuring[10]在研究FNN的构造方面做出了突出贡献,给出了一种连续模糊函数逼近器的FNN的构造方法。这些结果对实际系统设计中模糊函数的选取具有指导性的意义。
(3)关于FNN的学习能力
FNN的学习包括两个方面:一是有效的学习算法,二是学习的精度和普适性。通常,由于模糊运算的复杂性和一些算子的不连续性,在多层前向NN中常用的BP算法和其他一些优化算法不能直接用于多层前向FNN,而修改后的Fuzzy BP规则解决了此问题。为简化学习算法,FNN的许多学习算法都采用经验学习公式或规则,尽管缺乏完备的理论,但效果显著。
FNN的学习精度和函数逼近性能密切相关。尽管训练样本有限,但只要网络足够大,学习算法有效,达到高精度的学习目标并非难事。然而训练样本的有限性导致学习结果的普适性变差已成为学习的主要矛盾。目前关于FNN系统的普适性问题成果很少,因此,如何将非模糊学习机的普适性分析方法推广到模糊学习机,成为FNN学习问题研究的关键。
尽管这几年FNN成果不菲,但仍然存在如下问题:
①FNN模型的研究主要是NN的模糊化和FS的神经网络化,很少从人脑对模糊信息的处理机制上考虑问题。应从智能问题本身创造性地设计FNN模型,体现新的解决智能问题的思想。②FNN的数值计算导致严重的计算量问题。因此,有必要建立语言层次上的计算理论。③反馈FNN可以有效地解决成组、约束和动态学习以及空间关系学习等许多单项FNN很难解决的问题。因此,要加强反馈FNN的研究。
1.3 模糊专家系统
专家系统中模糊性的一个最主要表现就是模糊概念的存在。很好地表达模糊概念并不等于问题的根本解决,还要解决其使用问题。也就是在这样的专家系统中如何进行推理。这方面的成果不多,仅集中在专家系统中模糊概念的表达与推理方法的研究上。
1.4 模糊神经网络专家系统
专家系统的知识获取及经验性知识处理需要融合神经网络的高质量、高效率的学习能力与模糊逻辑出色的对于不完善知识的描述能力。发挥各自优势,能明显提高专家系统的性能。
(1)知识表示问题
在实际问题中含有大量的模糊知识,仅用传统的知识表示方法是不够的。因此,模糊规则和隶属函数的引入成为必然。
(2)信念传播问题
推理期间可能有多条相同结论的规则同时满足条件,在传统的专家系统中,总是采用最大优先级规则,误差较大。为了解决这个问题,采用神经网络进行推理,结论的可信度是各条规则结论可信度的组合,权系数是通过训练网络得到的。
(3)更有效的推理
由于推理是通过神经网络实现的,减少了规则匹配过程,从而加快了推理速度。
(4)学习问题
利用神经网络的学习能力可容易地求精模糊规则,从而提高系统的适应能力。
Zha[11]提出了一种神经模糊专家Petri网模型,Li[12]开发了一个混合智能系统,还有不少文献在这方面也作了相应的研究工作。
综上所述,以神经网络与专家系统的结合、模糊神经网络、模糊专家系统以及模糊神经网络专家系统四种类型为主的智能混合系统成果颇多,代表了目前智能混合系统发展的主流方向。所涉及的技术主要有专家系统、神经网络和模糊理论三种。但是智能混合系统绝不仅限于此,还有许多智能技术,如粗糙集、遗传算法、Petri网等也成为智能混合系统集成技术的研究热点,不少文献在这方面做出了突出的贡献。
2 成果总结及进一步的研究方向
目前,智能混合系统己经取得了许多成果,在众多领域中得到了相当成功的应用,解决了许多单一智能系统不能解决的复杂问题,并且正在向着更深的研究层次挺进。这些成果集中表现在以下方面。
(1)利用神经网络优良的自组织、自学习和自适应能力初步解决了专家系统知识获取的“瓶颈问题”。
(2)利用专家系统良好的解释机能较好地解释了神经网络的行为,弥补了神经网络中知识表达的“黑箱结构”。
(3)神经网络与专家系统混合的系统通过融合模糊逻辑进行知识描述与推理,明显地改善了专家系统的性能。
尽管智能混合系统的研究取得了许多瞩目的成果,但其理论体系还很不完善,需从以下几个方面进一步深入研究。
(1)立足于广义人工智能,以模拟自然智能为目的,从思维科学的角度出发,研究人类认知过程中抽象思维与形象思维在功能、知识表达、思维活动等方面的内在关系。
(2)智能混合系统需要统一的知识表示方法,需要研究接近于人类思维模式的知识表示机理。
(3)利用神经网络有效地进行知识获取。
(4)研究实用的神经网络推理及结果解释方法。
(5)将已取得的智能混合系统研究成果向其他智能形式的综合集成中推广,从而进行更广泛的智能系统集成方法研究。
3 结 论
智能混合系统研究应从人类智能行为本质入手,着眼于知识在人脑中表示、存储及实现各种人类思维方式的生理基础。随着对人类生物神经系统、思维模式的进一步认识,研究各种新的集成系统模型,实现大脑思维过程的模拟,进而实现整个自然智能的模拟,从而最终揭开智能的奥秘。
参考文献
1 Gallant I S.Connectionist expert systems.Communication of the ACM,1988;31(2):152
2 Caudill M.Using neural nets:Hybrid expert networks.AI Expert,1990;5(11):49
3 Kuncicky D C,Hruska S I,Lacher R C.Hybrid systems:the equivalence of rule-based expert systems and artificial neural network inference.Int.J.of Expert Systems,1991;4(3):281
4 Towell G G,Shavlik J W,Noordewier M O.Refinement of approximate domain theories by knowledge-based neural networks.In:Proc.AAAI-90,August,1990:861
5 Suddarth S C,Holden A D C.Symbolic-neural systems and the use of hints for developing comples systems.Int.J. Pattern Recognition,1991;5(4):503
6 Tirri H.Implementation expert system rule conditions by neural networks.New Generation Comput.,1991;10:55
7 Chen K H.A multiclass neural network classifier with fuzzy teaching inputs.Fuzzy Sets and Systems,1997;91:15
8 Carpenter G A,Grossberg A,Rosen D B.Fuzzy ART fast stable learning and categorization of analog patterns by an adaptive resonance systems.Neural Networks,1991;4:759
9 Buckley J J,Hayashi Y.Fuzzy neural networks:a survey. Fuzzy Sets and Systems,1994;66:1
10 Feuring T,Lippe W.The fuzzy neural network approximation lemma.Fuzzy Sets and Systems,1999;102:227

