MIMO系统利用多根收发天线进行无线信号的传输,极大地提高了系统的容量,改进了系统的性能,同时增加了接收端设计的复杂度。这与接收端设计的轻巧、节能等原则不符,考虑把接收端的处理工作转移到发射端,因此在MIMO系统引入了发射端的预编码。研究MIMO系统预编码的设计大多是基于频率非选择性衰落信道的假设。对于频率选择性MIMO信道的处理方法,常用的是MIMO-OFDM技术,该多载波方案虽然较为有效地消除了多径信道间的影响,但与此同时也带来了高峰均功比和对同步要求高等问题。OFDM可以看做是一种特殊的预编码技术,且最优空时预编码的性能与MIMO-OFDM是等价的,但是通常要进行高阶矩阵计算。因此,单载波传输方案仍被采用在LTE的上行链路中,研究频率选择性MIMO信道下单载波传输系统的预编码技术具有一定的实际意义。

    在非平坦MIMO信道下,由于没有一个空域预编码能够在空域把所有的可分辨多径矩阵信道正交化,因此频率平坦信道下的预编码系统不能直接应用于频率选择性信道下的单载波系统,这就决定了非平坦MIMO信道下的预编码技术研究与平坦衰落信道中的任务有所不同：消除共信道干扰（CCI）和符号间干扰（ISI）两种干扰、发射优化。对于频率选择性衰落MIMO信道,单载波传输系统的预编码设计,把选择性信道建模为Toeplitz矩阵,等效为线性处理[1],通过Z域变换把频率选择性MIMO信道描述为多项式矩阵,然后采用宽带特征分解方法[2]设计出空时联合发射预编码,从而将所有多径信道同时在空域进行正交化,把选择性信道转化为并行独立的非选择性信道。前两类研究并未解决多径矩阵分量的正交化问题,并且通过Z域处理进行正交化的处理仍存在单入单出（SISO）信道的ISI问题。
    针对以上问题,本文研究了频率选择性信道下单用户MIMO的联合收发设计问题。为了实现非平坦MIMO信道多径矩阵信道分量分离,借鉴参考文献[3]中的块对角化方法,提出了零空间（NS）联合设计方案,利用零空间的概念,在发射端和接收端均采用线性空间处理,进行收发联合设计。首先,计算各个时延信道矩阵对应的预编码矩阵,使得该子信道的预编码矩阵是其他所有子信道的共同零空间的标准正交基组成的矩阵。对于经过初步处理的信道,利用同样的方法,设计各时延子信道矩阵的接收处理矩阵。经过联合收发处理后的频率选择性信道,转化为若干空间正交的平坦衰落子信道,因此频率平坦信道下的预编码系统就可以直接应用于该频率选择性信道。理论分析和仿真结果表明，该算法解决了Z域分解方法[2]中未消除ISI的问题,具有相当的计算性能,并且在高信噪区域具有较高的容量。

\

4 仿真结果及数值分析
    下面对所提出的NS收发机设计进行仿真分析。假设发射的平均总功率为P,信噪比的定义为SNR=P/?滓2,频率选择性信道采用抽头时延模型,多径子信道的每个信道增益都是独立同分布的高斯随机变量,均值为0,方差为1。以参考文献[2]中的方法为参考方法,分别对L=2,3,4三种情况的零空间处理前后的信道容量进行了仿真,在同等采用格雷映射和QPSK调制的无编码系统,利用本文方法分离后的多径分量采用SVD“注水”型预编码进行处理。所有的结果都是对1 000次蒙特卡洛实验结果进行平均得到的。
    图1、图2和图3分别给出了L=2,3,4时的信道容量。在三幅图中可以看出,本文方法容量限始终高于参考方法容量；L确定时,不同天线配置的本文方法容量和参考方法容量变化趋势大致相同,但是两种配置之间的容量差越来越大；L不同时各种天线配置的容量变化关系趋于一致。本文方法容量高于参考方法容量有其理论解释,这是由于本文的处理是基于空间维度的处理,充分利用了系统设计的空间自由度,利用空间维度换取时延维度上的可分离性,实现了空间正交化,完成信道的平坦化处理。并且由于分离后的各个多径分量采用容量最佳的SVD预编码，带来了容量性能的提升。

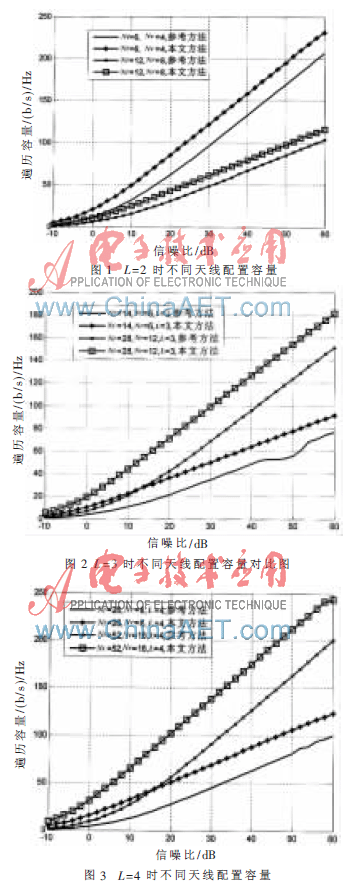
　    图4给出了图1、图2和图3中各种配置下本文方法容量限与参考方法容量之比随着信噪比的变化趋势。可以看出选择性信道多径分量数目L越大,低信噪比区域-10 dB~20 dB内,本文方法容量限与参考方法容量之比越大,进行正交化处理损失容量的比例越大。但是,无论多径分量的多寡与天线配置如何, 在高信噪比区域20 dB~60 dB内,本文方法容量限与参考方法容量之间的比例愈发趋于1的常数。这说明随着信噪比的增加,经过零空间处理的参考方法信道容量逐渐接近与本文方法容量限的某个比例。

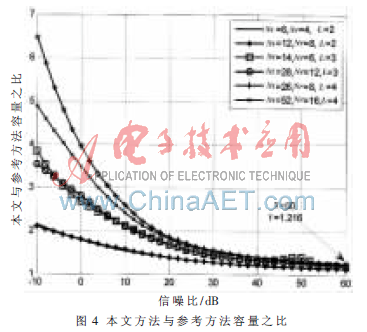
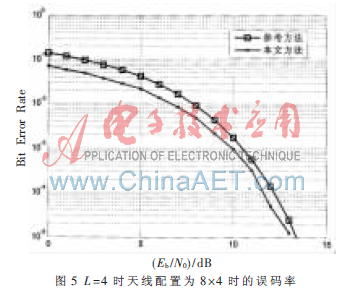
    图5是具有L=4条多径时，本文方法与参考方法误码率的对比。本文方法优于参考方法，这是由于前者进行了平坦化处理，并且每路多径采用SVD预编码，最终把选择性MIMO信道分解为若干独立的SISO信道，使得码间干扰为零，提高了误码率性能。获得高容量性能和误码率性能的代价是带来了复杂度的增加，复杂度为参考方法的L（多径数目）倍，本文方法与参考方法的相对复杂度如图6所示。复杂度的增加与多径数目近似正比，这在实际应用中是可以接受的。

    本文研究了频率选择性MIMO信道多径分离的问题。提出了一种基于预编码算法,把频率非平坦的多时延矩阵信道转化为了并行的平坦MIMO子信道,实现了各时延路径信道的空间正交化,把选择性信道的收发设计转化为了并行处理的传统非选择性MIMO信道收发设计,并且由于不进行迭代处理,因此具有较低的计算复杂度。这样就可以平坦衰落下的预编码研究成果直接应用于频率选择性MIMO信道中。仿真结果表明,所提出的算法在实现了多径在时延维度上的可分离性的同时, 解决了传统Z域处理中未消除ISI的问题,复杂度为Z域方法的L（多径数目）倍，具有较好容量性能和误码率性能。
参考文献
[1] IRMERR, BARRETO A N, FETTWEIS G. Transmitter precoding for spread-spectrum signals in frequency-selective fading channels[C]. Citeseer, 2001.
[2] MCWHIRTER J G, BAXTER P D, COOPER T, et al. An EVD algorithm for para-Hermitian polynomial matrices[J]. Signal Processing, IEEE Transactions on.2007,55(5):2158-2169.
[3] WANG F, BIALKOWSKI M E, LIU X. Performance of block diagonalization broadcasting scheme for multiuser MIMO system operating in presence of spatial correlation and mutual coupling[J]. International Journal of Communications, Network and System Sciences,2010,3(3):266-272.
[4] VU M, PAULRAJ A. MIMO wireless linear precoding[J]. Signal Processing Magazine, IEEE. 2007,24(5):86-105.
[5] TREFETHEN L N, BAU D. Numerical linear algebra[M]. philadelphia: Society for Industrial Mathematics, 1997.
[6] 刘毅. MIMO信道预编码技术研究[D]. 西安：西安电子科技大学, 2007.