一种基于小波降噪的GNSS轨迹平滑算法-AET-电子技术应用

一种基于小波降噪的GNSS轨迹平滑算法

来源：电子技术应用2012年第5期

李立言，赵民建，钟杰

浙江大学信息与电子工程学系，浙江杭州310027

摘要： 当载体具有高阶动态时，基于载波多普勒平滑伪距的解算误差扩大，且载体轨迹小波降噪处理结果会发生畸变。针对这些问题，提出了一种新的基于小波降噪载体位置平滑算法。算法对基于伪码测距和载波多普勒平滑伪距的解算结果进行差分，并根据差分值的频谱特征，选择合适的尺度进行小波降噪处理后,与基于载波多普勒平滑伪距的解算结果求和得到轨迹平滑结果。仿真结果表明，该算法在载体最大加加速度为50 m/s3的条件下，定位均值偏差小于0.04 m，标准差小于1.3 m。

关键词： 高动态 GNSS接收机小波降噪轨迹平滑

中图分类号： TN961
文献标识码： A
文章编号： 0258-7998(2012)05-0118-04

A GNSS track smoothing method based on wavelet de-noising

Li Liyan, Zhao Minjian, Zhong Jie

Department of Information Science and Electronic Engineering，Zhejiang University， Hangzhou 310027，China

Abstract： When user jerk increases, the estimation errors of both carrier Doppler smoothed pseudoranges based positioning and wavelet de-noising applied directly to track smoothing will become larger. A novel track smoothing method based on wavelet de-noising is proposed in this paper to solve these problems. Differential of the position estimations based on code generated pseudoranges and carrier Doppler smoothed pseudoranges is calculated. After wavelet de-noising of the differential, the sum of the result and the carrier Doppler smoothed pseudoranges based positioning is used as the smoothing result. Simulation result shows that estimation bias of the proposed method is less than 0.04 m and the standard deviation is less than 1.3 m when the user maximum jerk is 50 m/s3.

Key words : high dynamic； GNSS receiver； wavelet de-noising； track smoothing

小波域中各个尺度上信号大部分能量集中在信号突变位置，而噪声对应的小波系数在各个尺度上的分布均匀且幅值较小。参考文献[1]提出了基于小波系数阈值的降噪方法。非线性阈值估计器能够在多种不同类型信号条件下接近最小最大风险，具有比线性估计器更好的性能。

   在GNSS接收机中，卫星信号经过伪码相位估计、载波频偏估计及位置解算等处理后得到载体位置。不同的背景噪声和不同的信号处理算法都会影响估计误差特性，因此很难给出通用的载体位置解算误差模型或其近似描述。在低动态GNSS接收机中,为平滑载体运动轨迹，降低载体位置解算中的噪声，通常在获取载体速度估计后，采用卡尔曼滤波的方式达到位置平滑的目的[2]。但在高动态接收机中，载体高阶动态变化会导致对载体速度估计精度的下降。基于速度的轨迹平滑方法精度随之降低。同时，载体高阶动态可能导致载波相位跟踪环路的失锁或周跳。载波相位测量结果不能直接用于载体位置解算处理。
   参考文献[3]提出了一种基于载波多普勒的伪距平滑算法。算法通过对载波多普勒的数值积分替代载波相位的直接测量，实现了载波相位不可用条件下的伪距预处理。该算法在低动态条件下具有分米级的定位精度。但随载体动态提高，数值积分误差及环路频率跟踪误差放大使平滑伪距偏差增加，从而造成解算结果与真实值的偏差扩大。
    本文提出了一种新的基于小波降噪载体位置平滑算法。基于伪码测距的解算均值偏差较小但误差方差较大的特征，对基于载波多普勒平滑伪距的解算结果进行误差修正。利用位置差分的方式降低了待处理数据中的高频成分，降低小波降噪处理中的门限，从而提高了算法的噪声隔离性能。最后通过采集信号重构高动态场景对算法性能进行了仿真验证。
1 基于差分信号的轨迹平滑算法
    图1所示为载体具有加加速度条件下，基于伪码测距的解算、基于载波多普勒平滑伪距的解算及基于小波直接轨迹平滑得到的一组位置估计仿真结果。仿真中载体从第1 140 s开始进行变加速运动，其最大加加速度为50 m/s3。从图中可以看出，基于伪码测距的解算算法估计误差方差较大，而后两种算法在载体具有高阶动态时会发生误差扩大的现象，因此并不适合高动态条件下的应用。

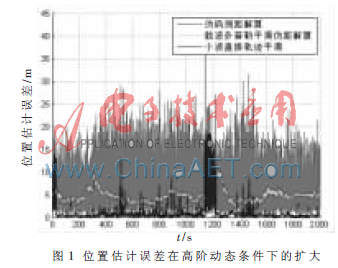
参考文献[4]提出的WaveSmoothTM算法通过对伪码测距与载波相位测距间偏差进行小波分析，选取合适的小波变换尺度和数据长度对信号进行降噪处理。具有较低的运算开销和较好的实时性能，并且比传统的时域平滑算法和频域滤波方法能够更好地滤除伪距测量中的低频噪声分量。
基于类似的想法，考虑应用小波降噪处理构成载体轨迹实时平滑算法。对基于伪码测距和载波多普勒平滑伪距的解算结果进行差分，以降低数据中的高阶变化。对差分结果进行小波降噪处理后，与基于载波多普勒平滑伪距的解算结果求和得到轨迹平滑结果。

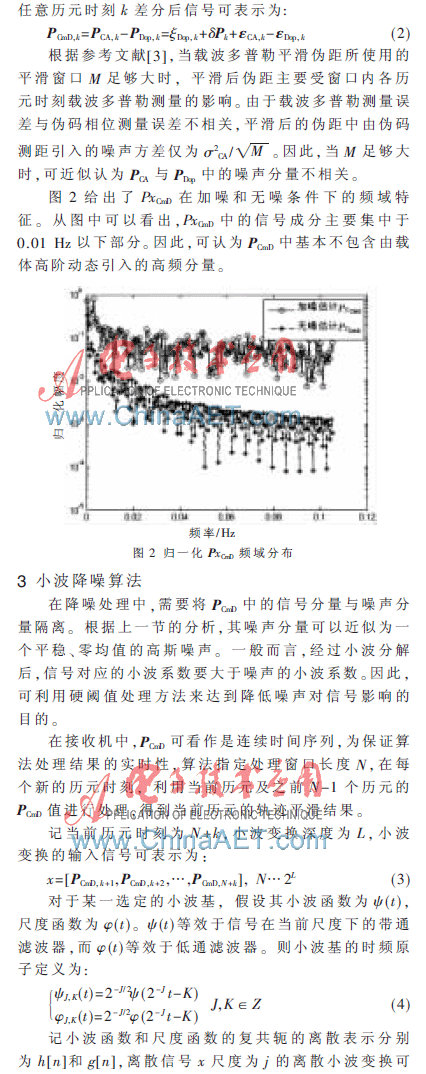
   算法平滑后载体位置估计精度如表1所示。可以看出，算法在高动态条件下载体位置估计误差均值基本为0，单轴标准差小于1 m，接近参考文献[3]中低动态条件下载波多普勒平滑伪距定位算法的性能。

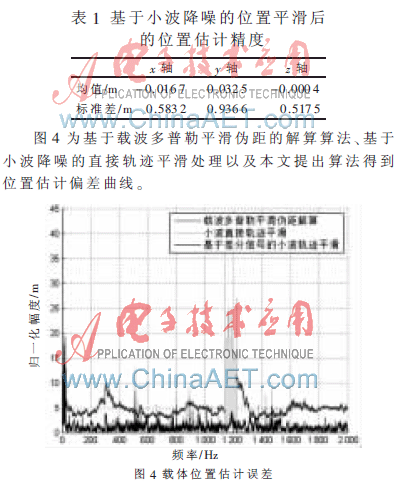
从图4中可以看出，基于小波降噪的直接轨迹平滑处理和本文提出的算法在位置估计均值精度上明显优于基于载波多普勒平滑伪距的解算算法。在第1 140 s前后，载体以较大加加速度运动时，受频率环稳态跟踪误差影响，载波多普勒平滑伪距定位算法位置估计误差发生扩散, 基于载波多普勒平滑伪距的解算算法位置估计误差逐步放大，直至第1 198 s载体转为匀速运动后误差逐渐缩小。而基于差分信号的小波轨迹平滑算法在整个定位过程中基本排除了上述原因引入位置估计误差，具有更好的性能。
在高动态条件下，载体动态会引起接收机中锁相环（PLL）的不稳定性，无法直接采用载波相位测距提高位置估计精度。而采用载波多普勒平滑伪距解算得到的位置存在较大的均值偏差。本文提出了一种基于差分信号的小波轨迹平滑算法。仿真表明，该算法在载体最大加加速度为50 m/s3的条件下，定位均值偏差小于0.04 m，标准差小于1.3 m，在高动态条件下具有较高的定位精度。
参考文献
[1] DONOHO D L. De-noising by soft-thresholding [J].IEEE Transactions on Information Theory, 1995,41(3):613-627.
[2] 谢钢. GPS原理与接收机设计[M]. 北京：电子工业出版社, 2009:128-129.
[3] BAH′RAMI M. Getting back on the sidewalk: Doppleraided autonomous positioning with single-frequency mass market receivers in urban areas[C].Proceedings of 22nd International Technical Meeting of the Satellite Division,Savannah, USA: Institute of Navigation, 2009:1716-1725.
[4] BARTONE C, ZHANG Y. A real-time hybrid-domain wave smooth code processing using wavelets[C]. Proceedings of 17th International Technical Meeting of the Satellite Division, Long Beach, USA: Institute of Navigation, 2004,436-446.
[5] 鲁郁. GPS全球定位接收机——原理与软件实现[M].北京: 电子工业出版社, 2009.
[6] 郑亚弟.导航载体轨迹仿真系统的研究与开发[D].郑州:解放军信息工程大学, 2006.
[7] DAUBECHIES I. Orthonormal bases of compactly supported wavelets [J]. Communications on pure and applied mathematics, 1988,41(7):909-996.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容