摘 要: 借鉴统计物理中对复杂系统自组织性的评估思想,基于协同进化的涌现方法,提出了一种通用的多主体系统中涌现行为的定量评估模型,并指出如何将该模型的评估值作为复杂系统进化的反馈。
关键词: 定量评估模型 多主体系统 协同进化算法
多主体系统MAS(Multi-Agent System)是目前人工智能、自适应控制等诸多领域的一个研究热点。作为复杂系统的一种抽象描述模型,MAS的涌现能力已特别引起研究者的关注。一般认为,具有涌现性的系统能通过由多个自主体的局部行为的相互作用得到系统的全局行为与目标,因而在理解各种复杂大规模问题的机理并加以求解方面具有十分重要的意义。
由于针对MAS涌现的研究目前主要集中在涌现方法上,对系统涌现行为的评估几乎空白。因此怎样进行MAS涌现行为的评估是一个亟待解决的问题。本文针对这一不足,提出一种通用的多主体系统中涌现行为的定量评估模型。该模型借鉴统计物理中对复杂系统自组织性的评估思想,基于协同进化的涌现方法,通过计算进化系统的复杂度来对系统整体进化行为进行评估。并且,对怎样将该模型的评估值作为复杂系统进化的反馈及对该模型的定量性、合理性和通用性进行了分析。实验结果证明,本文的方法可以对MAS涌现行为进行有效的评估。
1 系统的体系结构
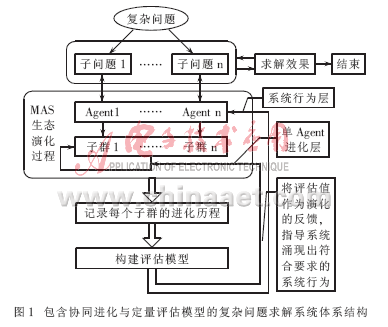
包含协同进化与定量评估模型的复杂问题求解系统的总体思想是:借鉴复杂性科学的研究思路,用生态种群协同进化实现系统行为的涌现,再用定量评估模型来指导系统的涌现过程,其体系结构如图1所示。

在涌现方法研究中,首先用MAS来对应复杂问题,然后建立一个生态多种群协同进化环境来对应MAS,再用生态种群协同进化来调控MAS的演化行为。在定量评估模型研究中,首先构建MAS的涌现评估模型,然后进一步利用评估结果作为涌现中Agent层和系统层的反馈来指导系统涌现出适当的整体行为。
2 多主体系统中涌现行为的定量评估模型
2.1 定量评估模型的构建
借鉴统计物理中对复杂系统自组织性的评估思想,参考Smith[3][4]等人定量评估抽象物理系统自组织性(复杂性)的方法,本文的MAS涌现定量评估模型按如下步骤构建。
(1)记录子群进化轨迹的矩阵
矩阵Z记录了系统中N个Agent经过M代的进化轨迹。

gi表示进化到第i代时,彼此之间相互关联的所有Agent的局部行为向量,即协同进化中第i代的所有子群个体特征向量;nij表示第j代中第i个Agent的个体特征值,这里可以用遗传算法中个体基因编码的函数表示。
该矩阵记录了每个子群的整个进化历程,提供了评估模型要分析的数据集合。
(2)计算矩阵的奇异值
奇异值的定义:设矩阵A∈Cm*n。A*A的特征值的非负平方根称作A的奇异值;A的奇异值的全体记作?滓(A)。
奇异值的定理:矩阵的非零奇异值的个数就等于矩阵的秩rank(A)。
按照奇异值的定义计算出矩阵Z的奇异值向量,然后按如下公式计算出![]() ′:
′:
![]()
由奇异值的定义及定理可以看出:复杂程度小的系统产生的矩阵对应的有意义的大于0的![]() ′值个数少,反之则多,这可以与复杂系统的熵相对应。
′值个数少,反之则多,这可以与复杂系统的熵相对应。
(3)计算熵
要通过矩阵的奇异值向量得到单一量化的值还需要进一步的计算。在上面的计算结果得到的向量![]() ′的基础上,用如下的公式计算出香农熵(shannon entrophy)S:
′的基础上,用如下的公式计算出香农熵(shannon entrophy)S:
![]()
(4)计算自由度
用如下的公式计算出自由度Ω:Ω=2S
计算的结果用于衡量系统复杂程度。
2.2 定量评估模型反馈指导演化涌现的方法
将评估模型与演化涌现结合,目的是用评估结果指导演化过程。
如图1所示,这里的反馈分二层进行:①将评估值反馈作用在系统行为层,可基于评估值对多Agent的关联特征参数作进一步优化,即调整子群间协同进化合作与竞争参数,从而获得满足要求的系统行为。②将评估值反馈作用在单Agent进化层次,对单Agent的局部进化参数作进一步优化,即调整单Agent选择、交叉、变异参数,从而获得满足要求的单Agent进化行为。
2.3 定量评估模型的分析
(1)定量性
不同于一般的定性分析,本文的模型基于动态系统理论,给出一种基于系统熵的定量评估方法。此方法的优点为:
①该定量评估模型依赖于多个Agent的局部进化行为、Agent之间的相互关联特征及生存环境(资源),可以分析评估值的变化与系统描述参数的对应关系及与系统各种行为的对应关系,从而可以定量评估系统涌现出的不同行为。
②可以考察模型中参数取值与系统整体行为的相互影响,找出系统行为转换的相变点或临界区域,深入探讨复杂系统的涌现机理。
(2)合理性
Smith等人提出的抽象物理系统中的定量评估模型[3][4]是以非线性的二维粒子的复杂运动为研究对象,构建记录系统粒子运动特性的矩阵。其中行向量记录了每个粒子的速度、位置属性;列向量记录了某一粒子某一属性随时间的变化情况。例如xi j、yi j、xi j、yi j,分别表示粒子j在第i时刻时x、y方向的位置、速度值。然后采用与上述模型类似的计算过程计算出系统的自由度,从而与不同的系统涌现行为相对应。实验证明,这种方法在抽象物理系统中是一种可行的系统涌现评估方法。
本文模型与Smith提出的模型的区别主要在构建记录子群进化轨迹的矩阵。通过分析基于生态种群协同进化方法实现的多主体系统的涌现行为,将所有粒子的运动属性对应到本文的MAS系统的单个Agent的局部行为向量;粒子间复杂的非线性关系对应到本文的单个Agent相互关联特性,即协同进化的合作与竞争关系;粒子随时间的位移对应到本文的MAS系统每一代的进化轨迹。
通过上述的对应关系,实现了抽象物理系统的定量评估方法与基于生态种群协同进化的MAS涌现方法的有效结合,从而充分体现了本文的MAS涌现行为的定量评估模型的合理性。
(3)通用性
从评估矩阵的构建和系统自由度的计算过程可以看出,评估结果只依赖于个体的局部状态变量,与具体进化算法无关。因此,只要个体的特性值选择合理,本文的模型对采用任意进化算法的MAS系统都是适用的。
3 实验结果分析
这里选取了二种不同的协同进化算法。一种算法使得每个Agent进化过程中采用的交叉、变异算子效果明显,另一种则相反。而且选择操作采用保留最佳个体的策略,然后按照上述评估模型求得系统自由度,即系统进化复杂程度分别为:系统1的Ω=1.3886e+105;系统2的Ω=1.8544e-040。
图2~图4给出了采用二种不同协同进化算法时,系统的求解效果、奇异值和子群进化曲线的比较。其中,图2记录了采用二种不同的协同进化算法,进化代数为100代时的进化结果图;图3记录了二种不同的协同进化条件下计算出的系统奇异值,纵坐标记录了奇异值的对数,并将100个奇异值按照从大到小的顺序排列;图4记录了采用二种不同的协同进化算法得到的所有Agent进化过程的特性值曲线,Agent数量为16,对应了每个小图的16条不同的曲线,曲线上的每一点对应了该Agent进化到当前代时的特性值。
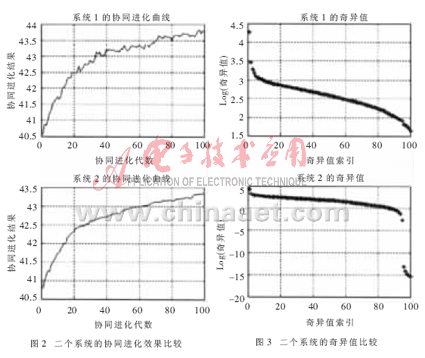
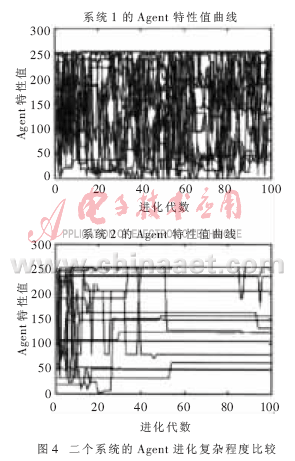
从图2中可以看出,这二种不同的协同进化系统求解的效果基本相同。但从图4中可以看出系统复杂程度有着显著的差别,系统1的复杂程度明显高于系统2,相应计算出的系统复杂性评估值Ω相差上百个数量级。从图3中可以看出,系统1中对系统复杂性评估产生重要作用的奇异值的个数(即奇异值取对数后值大于0的个数)明显多于系统2,其作用效果(即奇异值取对数后的值的大小)明显大于系统2。
将系统的奇异值曲线图、子群进化复杂程度曲线图和计算所得的系统进化复杂性程度评估值?赘相对照,可以得出以下结论:子群的进化曲线变化幅度大的系统奇异值的作用效果显著且有意义的奇异值个数较多,从而通过模型计算得到的系统复杂性评估值较大,反之则相反。因此本文的定量评估模型计算出的系统复杂性评估值有效地反映了实际系统的复杂程度。
4 结束语
目前国内外针对MAS的涌现研究主要集中在涌现方法上,对系统整体涌现行为如何评估几乎是空白。针对具体的复杂系统,系统的进化不仅要实现高效率,进化过程中系统的复杂程度也是衡量进化算法好坏的重要指标。本文的模型提出了一种解决此类问题的通用的方法。当然,目前的研究只是对这种将统计物理中有关复杂系统自组织性的评估应用到多主体系统定量评估的思想方法的初步尝试,提出的是一种通用的定量评估模型。
下一步的研究主要是针对特定的应用背景,具体实现本文的进化算法及在具体条件下Agent的相互关联特性和Agent的局部进化行为向量,构建评估矩阵并实现反馈,引导系统涌现出符合要求的整体行为。
参考文献
1 Yong C H,Miikkulainen R.Cooperative Coevolution of Multi-Agent Systems.Systems Technical,2001;Report AI01-287
2 Dagaeff T,Chantemargue F,Hirsbrunner B.Emergence-based Cooperation in a Multi-Agent System.In:Proceedings of the Second European Conference on Cognitive Science(ECCS′97).Manchester,U.K,1997
3 Wright W A,Smith R E,Danek M A et al.A Measure of Emergence in an Adapting,Multi-Agent Context.In:Proc. of 6th Int.Conf.of Simulation of Adaptive Behavior. Honolulu,USA,2000
4 Wright W A,Smith R E,Danek M.A Generalisable Measure of Self-Organization and emergence.In:Proceedings of Artificial Neural Networks.Springer Verlag,2001:857
5 Shimoyama N,Sugawara K,Mizuguchi T.Collective Motion in Systems of Mobile Elements.Physical Review Letters,1996;58:6480

