作 者:中南大学信息科学与工程学院 于 欣 王随平 张佳洁
引言
深海作业机器人是一种在水深5000~6000米的海底沉积物上行走、采集锰结核的智能履带车辆,两条履带由安装在后轮上的两台液压马达分别驱动,用变量泵调节速度。我国采矿区位于太平洋中部,为典型的深海平原,其上覆盖着很厚的淤泥及沉积物[1]。海底沉积物不同于陆地底质,剪切强度较低,具有搅动流体特性、塑性特性。如果深海作业机器人的行驶驱动力与沉积物特性不匹配,将出现履带过度打滑现象。为保证深海作业机器人的安全行走,应使行走驱动力适合沉积物特性的变化。基于上述问题,深海履带式作业机器人行走防滑控制技术的研究开发,将提升深海采矿系统安全作业水平。
国外机器人行走防滑技术的相关研究,daegun hong和paljoo yoon[2]提出了一种基于制动观测器的防滑控制系统。制动观测器负责评估车轮制动力,侧滑力和摩擦系数的变化。国内相关研究,刘志新、张大卫、李幼德[3]建立了四轮驱动汽车加速过程的数学模型,以滑转率为调节对象,提出一种基于模糊pid控制的驱动防滑控制asr算法。目前国内外对履带车辆防滑控制相关技术尚处于起步阶段,对复杂地形下的深海作业机器人,势必要求人们对机器人与地面相互作用特性,行驶底质识别以及防滑控制做更深入的研究,也必将促进人们对这些问题的认识。
本文根据深海作业机器人行走的特点和海底环境的特点,建立了深海作业机器人的力学模型,并根据机器人驱动系统的结构和特点建立了液压系统模型,设计了机器人防滑控制系统,并提出最佳滑转率的辨识方法。基于matlab仿真平台,对整个深海作业机器人防滑控制系统进行仿真。
深海作业机器人工作环境特性研究
(1)海泥土力学特性
深海作业机器人履带与海泥的作用十分复杂,图1为典型的海泥沉积物变形过程示意图,s为海泥应变,p为海泥所受压力。海泥受压时的破坏可分为三个过程[4]:
直线变形阶段(压密阶段):当履带对海泥的压载小于临界荷载时,海泥被压紧,地面能够表现为弹性状态。如图1示,a点之前。
局部剪切阶段(开始塑性变形):当履带对海泥的压载大于临界荷载而小于海泥的极限承载力时,海泥出现塑性变形,随着压力的增大,塑性变形区逐渐扩大。如图1示,a点与b点之间。
完全破坏阶段(塑性变形区连成连续的滑动面):当压力继续增大,超过海泥的极限承载力,塑性变形区连成连续的滑动面,海泥被挤出来。如图1示,超过“b”点后,应力增加一微小量,应变便显著增加。这种显著增加的应变,构成塑性流动。塑性流动以前的状态,通常称为塑性平衡状态。从塑性平衡状态转变为塑性流动状态,表示物质被破坏。
由以上分析可知,深海机器人应该工作在局部剪切阶段才能较好的利用海泥提供的牵引力行走。
(2)履带-海泥相互作用
当驱动履带,在接触面的地面上产生剪切作用。如图2所示,为了预测车辆的牵引力和滑转率,需要了解地面的剪切应力和剪切变形之间的关系。这个关系可由剪切试验来确定。在剪切试验中可用剪切板代替履带刺的剪切作用。
经测定我国矿区内的海泥剪切特性存在明显大于0的残余剪切力。wong提出以下公式来表示改型土壤:
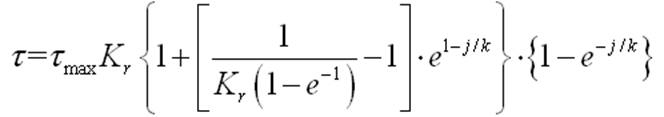 (1)
(1)
式中,k-水平剪切变形模数,m;j-剪切位移,m。kr-残余剪切应力与最大剪切应力比魊/鬽ax。
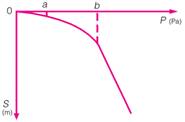
图1 海泥变形过程示意图
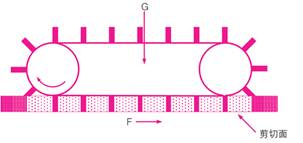
图2 履带的剪切作用
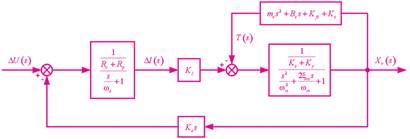
图3 比例阀传递函数框图
深海作业机器人模型
(1)深海作业机器人动力学模型
设机器车重心和几何中心重合,接地段的土壤特性为各向同性,履带接地段的负荷和土壤分布为均匀分布。
当机器车直线运行时,得单履带车体模型:
![]() (2)
(2)
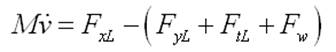 (3)
(3)
式中,m-深海机器人单侧模型质量,kg;j-履带驱动轮相对于转轴的转动惯量,kg·m2;ω-履带的转动角速度,rad/s;fxl-履带与海底地面间的附着力,n;fyl-履带的压实阻力,n;ftl-履带的推土阻力,n;fw-深海机器人海水阻力,n;tml-左履带马达驱动力矩,n·m;r-驱动有效半径,m。
(2)液压传动系统模型
在机器车行驶系统中采用变量泵-定量马达的容积调速回路。其中,电控变量泵由电液比例方向阀控制液压缸改变柱塞泵斜盘倾角的方式改变柱塞泵的排量,从而实现液压系统的流量控制。电液比例方向阀数学模型,采用电-机械转换元件直接驱动阀芯运动,从而将输入电压信号u转变为阀芯的位移量xv。
比例电磁铁控制线圈的端电压增量方程:
δu(s)=lsδi(s)+(rc+rp)δi(s)+kesxv(s) (4)
衔铁组件的动态力平衡方程:
kiδi(s)=mts2xv(s)+btsxv(s)+(ks+ky)xv(s)+t(s) (5)
阀芯动态力平衡方程:
t(s)=[mvs2+bvs+(kv+kfv)]xv(s) (6)
式中,l-线圈电感,h;rc,rp-线圈和放大器内阻,ω;ke-线圈感应反电动势系数,v;ki-比例电磁铁电流力增益,n/a;mt-衔铁组件质量,kg;bt-阻尼系数,n·s/m;ks-衔铁组件的弹簧刚度,n/m;mv-阀芯质量,kg;bv-阀芯的粘性阻尼系数,n·s/m;kv-阀芯对中弹簧刚度,n/m;kfv-作用于阀芯上的稳态液动力刚度系数,n/m;δi-线圈电流,a;ky-比例电磁铁的位移力增益和调零弹簧的刚度之和,n/m;t-衔铁外负载,n。
比例方向阀的模型框图如图3所示。
深海作业机器人防滑滑模变结构控制方法
(1)滑模切换函数
履带的纵向滑转率最好控制在略小于理想滑转率λt的一个小区域内,以便充分发挥履带的牵引能力,同时又能保证车辆具有一定的侧向性能。在实现防滑的滑模变结构控制时,若以履带纵向滑转率λ作为控制目标,设控制目标理想滑转率为λt,那么滑模变结构控制履带过度滑转实质上就是调节履带实际纵向滑转率与目标纵向滑转率λt之间的差值,并使之趋近于零。
控制的目标是寻找驱动力矩tm的控制规律,使得滑转率跟踪误差e趋向于零,设λt为海底行走最佳滑转率,则就是最佳滑转率对时间的导数。
假设最佳滑转率已知,控制的目的为控制驱动力矩的输入,使跟踪误差λ(t)-λt(t)趋近于零,所有状态变量有界。
滑模控制器应用切换函数来改变tm的控制规律,定义切换函数为:
![]() (7)
(7)
式中c1为待定系数,c1>0,e为驱动轮滑转率的误差变量,e=λ-λt
(2)基于μ-λ曲线形状的λt估计
通过分析可以提出λt的搜寻方法:
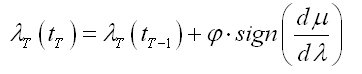 (8)
(8)
式中,φ是一符号为正的步进常数,当时,λt的值增加φ,同理,当时的λt的值减少φ。这样累计之后就能够得到系统的最佳滑转率。
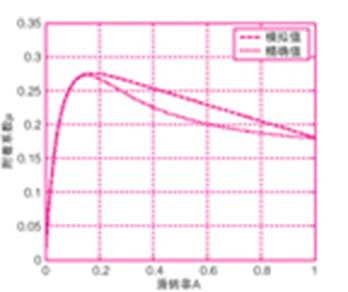
图4 不同行驶底质附着系数-滑转率关系图
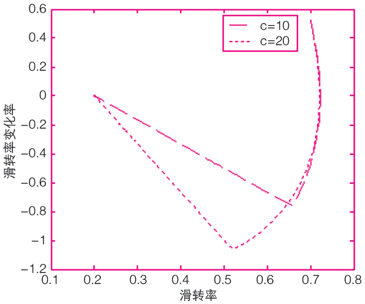
图5 滑转状态相轨迹图
仿真结果
(1)滑转率辨识仿真
图4中显示的是深海底附着系数-滑转率关系的拟合方法仿真结果。点虚线为根据附着系数定义由纵向牵引力得到的附着系数精确值c=2500;k=0.3;kr=0.45;a=3.25;g=50000;。划线虚线为根据burckhardt公式得到的拟合值,c1=0.3016;c2= 23.129;c3=0.121可以看出在附着系数的上升段拟合值和精确值几乎完全重合,该段对于最佳滑转率的识别是最有意义的一段,所以文中所用的拟合方法有很高的准确性。
(2)滑转率跟踪仿真
图5为滑转率跟踪控制的相轨迹图,如图中所示,在控制过程中,其相轨迹迅速趋于切换线,并在到达切换线之后将沿切换线快速滑向设定的理想值(λt,0),从而达到控制的要求。
结论
本文以深海作业机器人为研究对象,以车辆地面力学为基础,分析了深海作业机器人在深海底行走的特点,并在此基础上建立了作业机器人的动力学模型。分析了履带防滑控制的原理,确立了以滑转率控制为核心的控制方案。基于曲线形状的最佳滑转率辨识方法,根据附着系数对滑转率的导数正负来辨识滑转率的情况,从而推导出由可测参数马达转矩和履带角加速度来间接得到导数的正负值从而辨识出最佳滑转率值。以matlab为平台,对液压驱动系统进行了建模和仿真,验证所建模型的合理性。
作者简介
于欣(1986-) 女 硕士在读,研究领域:人工智能,计算机控制,深海机器人等。
参考文献
[1] 丁六怀,高宇清,简曲,等.中国大洋多金属结核集矿技术研究综述[j].矿业研究与开发,2003,23(4):5~8.
[2] daegun hong, paljoo yoon. wheel slip control systems utilizing the estimated tire force. minneapolis, minnesota, usa: the 2006 american control conference, 2006.
[3] 刘志新,张大卫,李幼德,等.基于滑转率的四轮驱动汽车防滑模糊控制仿真[j].农业机械学报,2005,36(12):21~24.
[4] 张克健.车辆地面力学[m].北京:国防工业出版社,2002.

