摘  要： 针对传统PID控制器在无刷直流电机控制时的鲁棒性差、精度低等缺点，在分析BLDCM数学模型的基础上，设计了RFBNN自适应PID控制器应用于无刷直流电机控制系统。通过Matlab/Simulink环境下的仿真实验表明，与传统的PID控制方法相比，该方法大大改善了系统的动态特性，减小了系统的稳态误差，提高了系统的自适应能力和抗干扰能力，满足了系统的控制性能要求。
关键词： 无刷直流电机；自适应控制；Matlab/Simulink

　无刷直流电机BLDCM（Brushless DC Motor）体积小、重量轻、效率高，在性能上保持了普通直流电动机的优点，且克服了有刷直流电机机械换向带来的一系列缺点，因此在国民经济的各个领域[1]得到广泛应用。
传统PID控制原理简单、使用方便，但依赖于被控对象精确的数学模型，对于无刷直流电机的多变量、非线性时变、强耦合的系统[2]难以达到很好的控制效果。本文将RBF神经网络自适应算法应用于PID控制中，能够有效克服传统PID控制器在被控对象具有非线性、时变不确定性和难以建立精确的数学模型时出现的参数整定不良和性能欠缺等缺陷，具有强鲁棒性和好的自适应性，使控制器适应被控对象参数的任何变化，能达到很好的控制效果。
1 BLDCM的数学模型
　无刷直流电机[3-4]可以看作是一台用电子换相装置取代机械换相的直流电动机，它由电动机本体、驱动控制电路和转子位置检测器等主要部分构成，其原理框图如图1所示。

　无刷直流电机采用两两导通的三相六状态的通电方式，为简化模型的建立和分析，作如下假设：
　（1）磁路不饱和，不计涡流和磁滞损耗。
　（2）忽略齿槽效应，三相对称的星形绕组均匀分布于光滑定子内表面。
　（3）不考虑电枢反应，气隙磁场分布近似梯形波，平顶宽度近似120°电角度。
　（4）转子上没有阻尼绕组，永磁体不起阻尼作用。
　则三相电压平衡方程为：


2.2 RBF神经网络
　RBF网络是一种三层前向网络，由输入层、隐含层和输出层组成。从输入层到隐含层的变换函数的映射为非线性，从隐含层到输出层的映射为线性，可通过调整权系数来改变网络的输出，从而加快学习速度，避免局部极小值的问题。其拓扑结构如图3所示。

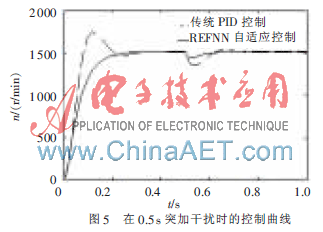
    从图4、图5可以看出，本文设计的基于RBFNN自适应PID控制方法，不仅使无刷直流电机调速系统的响应速度快、超调量小、控制精度高，且对外界干扰波动很小，自适应能力很强，稳定性能好。

    针对无刷直流电机转速控制中的高度非线性时变性、多变量难以控制的问题，本文提出了基于RBFNN自适应PID控制的方法。该方法充分利用了RBF神经网络的非线性逼近能力强，实时性好，输出误差小等优点，实时地调整PID控制参数以实现最优控制。Matlab仿真结果表明，该控制方法不仅使系统达到了较好的动静态特性，而且在突加负载情况，控制器仍能保持较好的控制效果，使系统具有便强的自适应能力。
参考文献
[1] FURUHASHI T. A position-and-velocity sensorless control for brushless DC motors using an adaptive sliding mode observer[J]. IEEE Transactions on Industrial Electronics， 1992，39（2）：89-95．
[2] PILLAY P， MODELING K R. Simulation and analysis of permanent magnet motor drives[J]． IEEE Transactions on Industry Applications，1989，25（2）：265-273．
[3] 高瑾，胡育文，黄文新．基于反电势形状函数法的无刷直流电动机直接转矩控制[J]．南京航空航天大学学报，2007，39（4）：417-422．
[4] 张琛．直流无刷电动机原理及应用[M]．北京：机械工业出版社，2004．
[5] 林嘉宇，刘荧.RBF神经网络梯度下降训练方法的学习步长优化[J].信号处理，2002，18（1）：43-48．
[6] 刘海珊，陈宇晨．无刷直流电机PID控制系统仿真及实验研究[J]．系统仿真学报，2009，21（16）：5157-5160．