摘 要: 对于使用支持NVIDA CUDA程序设计模型的GPU的二维一层浅水系统,给出了如何加速平衡性良好的有限体积模式的数值解,同时给出并实现了在单双浮点精度下使用CUDA模型利用潜在数据并行的算法。数值实验表明,CUDA体系结构的求解程序比CPU并行实现求解程序高效。
关键词: GPU;浅水系统;OpenMP;CUDA
以具有源项的守恒定律形式表达的浅水方程广泛用于引力影响下的一层流体建模,这些模型的数值解有许多用途,有关地面水流,如河流或溃坝水流的数值模拟。由于范围广,这些模拟需要大量的计算,因此需要很有效的求解程序在合理的执行时间内求解这些问题。
因为浅水系统的数值解有许多可开发的并行性,使用并行硬件可增加数值模拟速度。参考文献[1]给出了对于PC集群模拟浅水系统的数值模式和该模式的有效并行实现。参考文献[2]通过使用SSE优化的软件模块,改进了这个并行实现。尽管这些改进能在更快的计算时间内获得结果,但模拟过程仍需要很长的运行时间。
现代图形处理单元GPUs为以并行方式进行大规模浮点操作提供了数以百计的优化处理单元,GPUs也可成为一种在复杂计算任务中大大提高性能的简便而有效的方法[3]。
曾有人建议将浅水数值求解程序放在GPU平台上。为了模拟一层浅水系统,在一个NVIDIA GeForce 7800 GTX显卡上实现了一个明确的中心迎风方法[4],并且相对于一个CPU实现,其加速比从15到30。参考文献[1]在GPUs上所给数值模式的有效实现在参考文献[5]中有相关描述。 相对于一个单处理器实现,在一个NVIDIA GeForce 8800 Ultra显卡上得到了两个数量级的加速。这些先前的建议是基于OpenGL图形应用程序接口[6]和Cg着色语言(动画着色语言)的[7]。
近来,NVIDIA开发了CUDA程序设计工具包,以C语言为开发环境,对一般目的的应用,使GPU的程序设计更为简便。
本文目标是通过使用支持CUDA的GPUs加速浅水系统的数值求解,特别是为了取得更快的响应时间,修改参考文献[1]和参考文献[5]中并行化的一层浅水数值求解程序,以适应CUDA体系结构。
1 数值模式
一层浅水系统是一个具有源项的守恒定律系统,该系统可以为在引力加速度g作用下的占有一定空间的均匀流动的浅水层建模。系统形式如下:
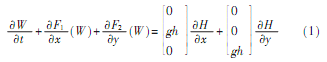
其中,



将在GPU上执行的每个处理步骤分配到同一个CUDA核,核是在GPU上执行的一个函数,其在执行中形成并行运算的线程块[9],算法实现步骤如下:
(1)建立数据结构
对于每个体积,存储它的状态(h、qx、qy)和高度H。定义一个float4类型的数组,其中每个元素表示一个体积并且包含了以前的参数,因为每个边(线程)仅需要它的两个相邻的体积的数据,将数组存储为一个二维纹理,纹理存储器特别适合每个线程在它周围环境进行存取。另一方面,当每个线程需要存取位于全局内存的许多邻近元素时,每个共享内存块更适合,每个线程块将这些元素的一小部分装入共享内存。欲实现两个版本(使用二维纹理和使用共享内存),用二维纹理可使执行时间更短。
体积区域和垂直水平边的长度需要预先计算,并传递到需要它们的CUDA核。运行时通过检查网格中线程的位置,能知道一个边或体积是否是一个边界和一个边的?浊ij值。
(2)处理垂直边和水平边
将边分成垂直边和水平边进行处理。垂直边?浊ij,y=0,水平边?浊ij,x=0。在垂直和水平边处理中,每个线程分别代表一个垂直和水平边,计算它对邻近体积的贡献在2.1节已描述。
当借助于存储在全局内存的两个累加器驱动一个特定的体积时,边(即线程)彼此相互同步,并且每个边都是float4类型的数组元素。每个累加器的大小就是体积值。累加器的每个元素存储边对体积的贡献(一个3×1向量Mi和一个float值Zi)。在垂直边的处理中,每个边将贡献写入第一个累加器的右面体积和第二个累加器的左面体积。水平边的处理与垂直边处理类似,只是加入累加器的贡献不同。图2和图3分别显示了垂直边和水平边的处理情况。
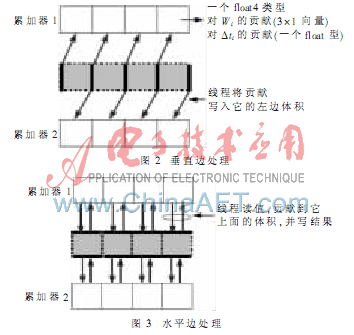
(3)为每个体积计算?驻ti
每个线程代表一个体积,正像2.1节描述的计算体积Vi的局部值Δti。最终将通过把存储在两个累加器中的相应体积Vi位置的两个float值相加获得Zi值。
(4)获得最小Δt
通过在GPU上应用规约算法寻找体积的局部?驻ti的最小值,所应用的规约算法是CUDA软件开发工具中所包含的规约样例的核7(最优化的一个)。
(5)为每个体积计算Win+1
在这一步,每个线程代表一个体积,正如2.1节描述的修改体积Vi的状态Wi。通过两个3×1向量相加求出Mi的最终值,这两个向量存储在与两个累加器的体积Vi相称的位置。因为一个CUDA的核函数不能直接写进纹理,需要通过将结果写进一个临时数组来修改纹理,然后将这个数组复制到绑定纹理的CUDA数组。
这个CUDA算法的双精度(double)版本已实现,以上所描述的有关实现的差别是需要使用两个double2类型元素的数组存储体积数据,并需要使用double2类型元素的4个累加器。

数值模式运行在不同的网格。在[0,1]时间间隔内,执行模拟系统。CFL参数是?酌=0.9,并且需要考虑墙壁边界条件(q·η)。
已经实现了CUDA算法的一个串行和四核CPU并行版本(使用OpenMP[8]),两个版本都使用C++实现,且使用矩阵操作本征库[10],在CPU上已经使用了double数据类型。将CUDA实现与参考文献[5]中描述的Cg程序进行比较。
所有程序都是在一个具有4 GB内存的酷睿i7920处理器上执行,所使用的显卡是GeForece GTX260和GeForce GTX280。表1显示了所有网格和程序的执行时间(由于没有足够的内存,有些情况不能执行)。
在具有两种显卡的所有情况下,单精度CUDA程序(CUSP)的执行时间超过Cg程序的执行时间。使用一个GeForce GTX280,相对于单核版本,CUSP实现了超过140的加速。对于复杂问题在两种显卡下,双精度CUDA程序(CUDP)比CUSP程序的执行速度慢7倍。正如预期的一样,相对于单核版本,OpenMP版本仅实现了不足4倍的加速(OpenMP版本的执行速度比单核版本快不到4倍)。
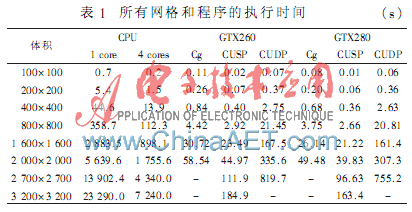
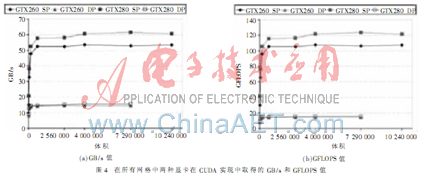
图4以图形的方式显示了两种显卡在CUDA实现中取得的GB/s和GFLOPS值。用GTX280显卡,对于大的网格,CUSP达到了61 GB/s和123 GFLOPS。理论最大值是:对于GTX280显卡,GB/s和GFLOPS值分别为141.7 GB/s、933.1 GFLOPS(单精度)、77.8 GFLOPS(双精度);对于GTX260显卡,GB/s和GFLOPS值分别为111.9 GB/s、804.8 GFLOPS(单精度)、67.1 GFLOPS(双精度)。
比较了在单核和CUDA程序求得的数值解,计算出了全部网格(t=1.0时)在CPU和GPU中得出的解之间的不同L1范数。使用CUSP的L1范数的数量级在10-2~10-4之间变化,而使用CUDP所得到的数量级在10-13~10-14之间变化,这反映了在GPU上使用单双精度计算数值解的不同精度。
使用CUDA框架为一层浅水系统建立和实现了一个有效的一阶良好有限体积求解程序。为了在CUDA体系结构上有效地并行数值模式,这个求解程序实现了优化技术。在一个GeForce GTX280显卡上使用单精度执行的模拟达到了61 GB/s和123 GFLOPS,比一个单核版本的求解程序快了2个数量级,也比一个基于图形语言的GPU版本速度快。这些模拟也显示了用求解程序所得到的数值解对于实际应用是足够精确的,用双精度比用单精度求得的解更精确。对于未来的工作,我们提出了在不规则网格上进行有效模拟的扩展策略,给出两层浅水系统的模拟。
参考文献
[1] CASTRO M J,GARCFA-RODRIGUEZ J A.A parallel 2D finite volume scheme for solving systems of balance laws with nonconservative products:application to shallow flows[J]. Comput Methods Appl Mech Eng,2006,195(19):2788-2815.
[2] CASTRO M J,GARCFA-RODRIGUEZ J A.Solving shallow water systems in 2D domains using finite volume methods and multimedia SSE instructions[J].Comput Appl Math,2008,221(1):16-32.
[3] RUMPF M,STRZODKA R.Graphics processor units:new prospects for parallel computing[J].Lecture notes in computational science and engineering,2006,51(1):89-132.
[4] HAGEN T R,HJELMERVIK J M,LIE K-A.Visual simulation of shallow-water waves[J].Simul Model Pract Theory,2005,13(8):716-726.
[5] LASTRA M,MANTAS J M,URENA C.Simulation of shallow water systems using graphics processing units[J].Math Comput Simul,2009,80(3):598-618.
[6] SHREINER D,WOO M,NEIDER J.OpenGL programming guide:the official guide to learning OpenGL,Version2.1[M]. ddison-Wesley Professional,2007.
[7] FERNANDO R,KILGARD M J.The Cg tutorial:the definitive guide to programmable real-time graphics[M].Addison Wesley,2003.
[8] CHAPMAN B,JOST G,DAVID J.Using OpenMP:portable shared memory parallel programming[M].The MIT Press,Cambridge 2007.
[9] NVIDIA.CUDA Zone[EB/OL].[2009-09-10].http://www.nvidia.com/object/cuda_home.html.
[10] Eigen2.0.9[EB/OL].[2009-09-10].http://eigen.tuxfamily.org.

