基于粒子群算法的盲多用户检测器-AET-电子技术应用

基于粒子群算法的盲多用户检测器

来源：电子技术应用2012年第6期

向志军1, 张群慧2

1. 湖南水利水电职院, 湖南长沙410131； 2. 湖南信息科学职业学院, 湖南长沙410151

摘要： 在信道参数未知的多径环境下,盲多用户检测算法性能存在诸如收敛速度慢和估计精度低等问题。将粒子群算法运用到基于恒模算法的盲多用户检测中。仿真结果显示，粒子群算法能够更精确地估计出信道的参数，且其收敛速度非常快，在估计出信道参数之后再进行盲多用户检测，检测性能优良。

关键词： 盲多用户检测粒子群算法恒模算法

中图分类号： TN914.5
文献标识码： A
文章编号： 0258-7998(2012)06-0115-03

The blind multiuser detector based on particle swarm optimization algorithm

Xiang Zhijun1, Zhang Qunhui2

1. Hunan Hydraulic and Hydroelectric College, Changsha 410131, China; 2. Hunan Information Science Vocational College, Changsha 410151, China

Abstract： The current blind multiuser detection algorithms’ capability is limited by many factors in multipath system whose channel parameter are unknown, the most important one of these factors is the estimation of channel parameter. Owing to the multiple access interference(MAI), it’s difficult to deal with channel estimation, the existing blind multiuser detection algorithms have some disadvantages such as slow convergence and low estimation precision. In this paper, we use particle swarm optimization(PSO) to deal with blind multiuser detection based on constant modulus algorithm(CMA), the emulation result shows that PSO performs well in blind multiuser dectection because of well performance in channel estimation.

Key words : blind multiuser detection algorithm; particle swarm optimization(PSO); constant modulus algorithm(CMA)

盲多用户检测[1]只需要知道期望用户的扩频码以及定时信息就可以抑制扩频通信中的多址干扰（MAI），一直是通信领域的研究热点。而在多径信道中,基于恒模算法的盲多用户检测器受到最为广泛的关注[2-4]。

    粒子群优化算法PSO（Particle Swarm Optimization）是一种源于人工生命和演化计算理论的优化技术，通过粒子搜寻自身的个体最优解和整个粒子群的全局最优解来更新完成优化[5-9]，在很多领域得到了应用。本文将粒子群算法运用到基于恒模算法的盲多用户检测中，利用其优异的搜索能力进行信道估计，完成盲检测。仿真结果显示，粒子群算法所得到的信道估计的MMSE可以达到10-5，收敛速度很快，检测性能理想。
1 多径条件下的CDMA系统模型
    考虑一个用户总数为j的CDMA系统，第j个用户的符号用长度为P的扩频码cj(k)进行扩频，随后再通过一个信道参数为gj(n)的多径信道。假设所有用户的最大的信道阶数为q，各用户的信息序列独立同分布，在接收端，用户j的离散码片采样信号yj(n)为符号序列ωj(n)和复合信道sj(n)的卷积为：

    基于粒子群算法的盲多用户检测器的流程如下：
   (1) 设置粒子群的个数并对所有粒子初始化，并初始化Pbest和Gbest。
   (2) 开始接收数据，对于每一个接收信号矢量yn：
   ①根据矩阵求逆引理自适应计算R-1；
   ②根据式(9)计算Gbest的适应值；
   ③根据式(9)计算每个粒子的适应值并更新其Pbest的适应值；
    ④根据式(7)更新每个粒子的位置和速度；
   ⑤将每个粒子的Pbest与Gbest比较，如果小于，则更新Gbest为Pbest；
    ⑥如果迭代次数达到Nmax或者Gbest的适应值小于Vmin，开始接收下一个数据矢量，否则回到②继续迭代；
   (3) 如果接收数据完毕，则迭代结束，否则返回步骤(2)。
4 仿真结果
    本文用Matlab软件进行仿真,在CDMA系统中有5个干扰用户，4个干扰用户相对于期望用户的MAI为10 dB，1个干扰用户的MAI为20 dB，扩频码长度为31的Gold码；期望用户与高斯白噪声的信噪比为20 dB；信道的多径个数为6个，所有用户的第一条路径的信道幅度衰落为0 dB，期望用户的第一条路径的延时为0，其余路径的延时为1~P-1之间的平均分布，信道衰落服从方差为1的高斯分布；信号的符号个数为2000，v为2；所有的Pbest以及Gbest的初始值都是[1,0,…,0]T，w从0.9均匀降至0.4，c1和c2为2；仿真次数为100次。
   图1给出迭代次数为10时，不同的粒子个数对信道估计的影响，可以看到当粒子个数为10时，再增加粒子个数对算法的性能提高已经很小了，将粒子个数设为10是较好的选择。图2给出不同的迭代次数Nmax对算法的影响，可以看到，Nmax为10时效果已经足够好，如果再加大Nmax，反而会因为迭代过多而造成性能损失。

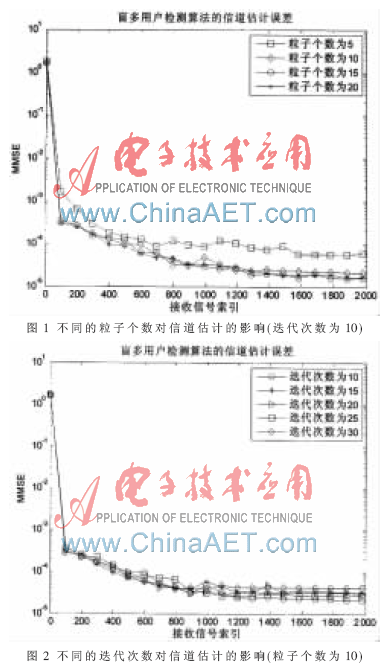
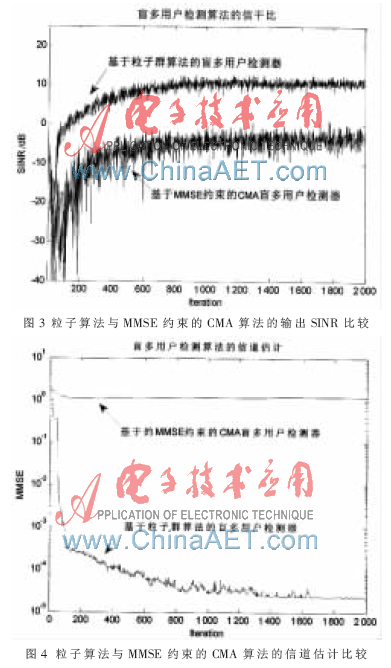
图3和图4显示的是迭代次数为10时10个粒子的粒子群算法与基于MMSE约束的CMA算法的比较。从图中可以看出，粒子群算法的性能远远好于基于MMSE约束的CMA算法，这主要是其信道估计的准确性更为优良。另外期望用户信息序列具有单位能量和信道参数g1的模为1这两个条件在仿真中都不满足，所以后者在仿真中的性能达不到参考文献[2]中的效果。

本文针对目前的盲多用户检测算法在信道参数未知的多径环境下的不足，将粒子群算法运用到盲多用户检测中。仿真试验表明粒子群算法具有理想性能。但是粒子群算法也有一些不足之处，一是运算量比较大，二是粒子群算法目前还未有成熟的理论分析，只能靠仿真进行研究，这些问题有待于更深入的研究。
参考文献
[1] HONIG M, VERDU S. Blind adaptive multiuser detection[J]. IEEE Transactions on Information Theory, 1995，41(4):944-960.
[2] Liu Ping, Xu Zhengyuan. Blind MMSE-constrained multiuser detection[J]. IEEE Transactions on Vehicular Technology. 2008,57(1): 608-615.
[3] WHITEHEAD J B, TAKAWIRA F. Performance analysis of the linearly constrained constant modulus algorithm-based multiuser detector[J]. IEEE Transactions on Signal Processing, 2005,53(2):643-653.
[4] GELLI G, PAURA L, VERDE F. A two-stage CMA-based receiver for blind joint equalization and multiuser detection in high data-rate DS-CDMA systems[J]. 2004,3(4):1209-1223.
[5] 董元，王勇，易克初.粒子群优化算法发展综述[J].商洛学院学报, 2006,24(4):28-33.
[6] SOO K K, SIU Y M, CHAN W S, et al. Particle-swarm optimization-based multiuser detector for CDMA communications[J]. IEEE Transactions on Vehicular Technology, 2007, 56(5):3006-3013.
[7] Chen Pohung. Pumped-storage scheduling using evolutionary particle swarm optimization[J]. IEEE Transactions on Energy Conversion, 2008,23(1):294-301.
[8] LIU Z, JI T Y, TANG W H, et al. Optimal harmonic estimation using a particle swarm optimizer[J]. IEEE Transactions on Power Delivery, 2008,23(2):1166-1174.
[9] 张晓东，李小平，王茜，等.服务工作流的混合粒子群调度算法[J].通信学报，2008,29(8):87-99.
[10] 谢晓锋，张文俊，杨之廉.微粒群算法综述[J].控制与决策，2003,18(2):129-134.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容