摘  要： 根据谱相关函数理论，对常用通信信号的谱相关函数和谱相关平面图的分析，提取4个可用于调制信号识别的谱相关特征参数。分类器算法采用改进的RBF神经网络。利用提出的联合特征参数和分类器算法能动态识别信号的调制方式。仿真结果表明，该算法在不增加算法复杂度的前提下，在低信噪比下能够取得较高的正确识别率。
关键词： 谱相关；径向神经网络；调制方式识别；识别概率；特征参数

　　调制模式识别又称为信号调制模式盲检测或信号分类等，其基本任务是对未知信号的通带调制模式进行分析、判决和归类。20世纪后期，随着计算机、通信技术的迅猛发展，军事和民用领域对调制模式的自动识别技术都产生了巨大需求，各国研究人员从信号分析和模式识别两方面进行了大量的研究。谱相关理论就是在这个时期由Gardner W A提出的[1-2]。
　　谱相关函数是功率谱密度函数的推广，但它又优于功率谱密度函数，利用谱相关函数的特性，例如谱相关函数对高斯噪声的不敏感性，可以在信噪比很低的情况下对信号进行处理，即在干扰和噪声背景下对信号进行检测、分类、参数估计及信号提取，其检测与估计性能比常规的谱分析方法要优越[3]。
　　本文将调制信号建模成循环平稳随机过程，利用信号的循环平稳特性及周期谱相关函数的特点，提取出反映信号差异的特征参数，并做了仿真分析和比较。在识别过程中，考虑到RBF神经网络是一种局部逼近网络，训练速度快，在逼近能力、分类能力和收敛速度等方面均优于BP神经网络[4]，由此引入改进的RBF神经网络对信号进行调制模式识别。仿真结果表明，该算法可有效识别所指定的调制方式，并在低信噪比下可得到较高的正确检测概率。
1 特征参数提取算法
　　本文利用信号的循环平稳特性，提取信号循环谱的有关特征参数。因所使用的识别算法以循环谱算法为基础，所以要先对信号的循环谱算法进行选择。
　　在目前所提出的诸多循环谱估计算法中，比较实用的算法有3种：频域平滑算法中的谱平滑算法(FSM)、时域平滑算法中的FFT累加算法(FAM)和分段谱相关函数算法(SSCA)[5]。本文对这3种算法的运算复杂度进行了比较，结果如表1所示。

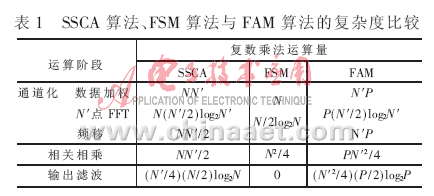
表中，P=N/L，N为整个采样数据长度，P表示抽取后的数据长度，N′为窄带滤波器数，L为抽取因子。
　　参看表1可知，FSM算法的运算量比其他两种算法的大很多，因此在这里不采用该算法。而SSCA算法在算法结构和硬件实现的复杂度方面比FAM算法更具有优势，在算法复杂度方面SSCA算法也占有优势。因此本文选择SSCA算法作为计算循环谱的算法。其表达式为[6]：

　　因篇幅有限在此仅给出BPSK信号的循环谱仿真图，如图1所示。

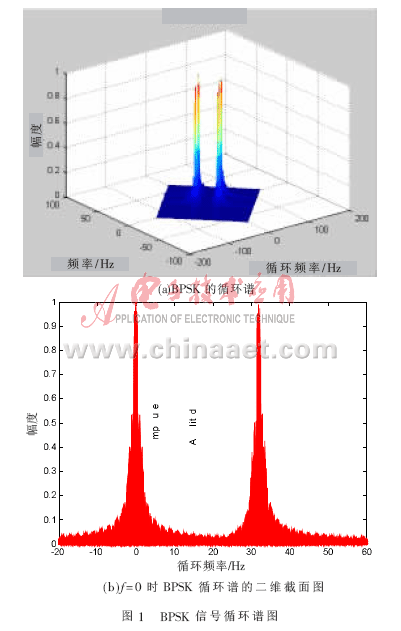
    　分析5种调制信号的谱相关函数及谱相关平面图可知，不同调制信号的谱相关函数有着显著的差别，主要表现在周期谱的幅度-双频(f，α)图的α轴与f轴上。同时经过大量的仿真和计算发现，QPSK信号的周期谱线幅度相对于其他4种信号要小得多，因此可以用在?琢轴上的周期谱线幅度来代替在α轴上的周期谱线平均能量这个参数，这样可以减少算法流程和系统中的计算量。综上所述，选择以下4个参数作为信号调制识别的特征参数：

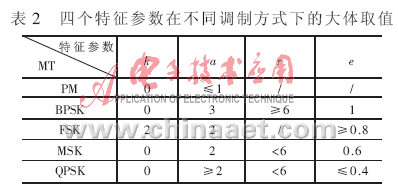
    表2给出以上4种特征参数在不同调制方式下的大体取值。表中参数获取时的原始数据均为归一化数据，表中“/”表示相应参数数据随信噪比或数据窗长的变化不稳定。

　　由以上得到的参数组成1个特征向量，定义为=[k，a，r，e]，此向量将作为RBF神经网络的输入参数，对调制方式进行识别。
2 改进的径向基神经网络分类器算法
　　本文采用RBF神经网络分类器。分类器采用神经网络的原则就是得到最大的正确识别概率和最优的均方误差(SSE)。这2个性能指标主要由神经网络的大小、训练样本、训练算法和激励函数决定。在满足性能的基础上，神经网络的收敛性由神经网络的层数和输出节点决定，而训练样本的数量和质量能够在很大程度上影响神经网络的识别精度，本文将针对以上因素对网络做出一些改进以提高网络性能，所要识别5种调制类型如表3所示。

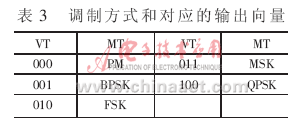
　　按常规的神经网络共需5个输出，但本课题利用3个输出，以减少输出节点，加快神经网络的收敛性，提高神经网络的性能，同时也降低网络的复杂度。其输出向量VT和所对应的调制方式如表3所示，MT代表调制方式。
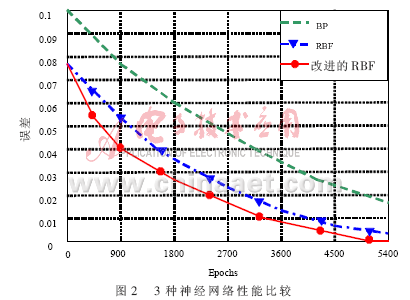
　　图2给出了采用BP神经网络、RBF神经网络、改进RBF神经网络的训练步数和误差之间的关系，从图中可以明显看出，改进的RBF神经网络比BP神经网络和传统RBF神经网络的性能有明显改善。

3 仿真结果及性能分析
　　为验证算法及其性能，对表3中所列的5种调制信号用Matlab进行仿真。接收机的中频为10 kHz，带宽为20 kHz，取样频率为40 kHz，已调信号码元速率为1 200 b/s。
　　仿真信噪比从-5 dB~20 dB，每5 dB评估1次识别率，每种调制信号共产生216组不同的数据。PM信号调制指数范围取[1，2，3，4，5，6]，数字信号应用升余弦脉冲成形滤波器控制带宽，滚降系数范围取为[0.3，0.35，0.4，0.5，0.6，0.65]，每个信号段取8 192个样点。根据不同的信噪比、调制指数以及随机选取的信号段，可以得到共1 080组不同的数据，经过特征提取可以得到900组不同的特征值作为神经网络的训练样本。180组不同的特征值作为神经网络的测试样本。获得训练样本之后，需要对数据进行归一化处理。RBF网络的构造函数为：newrb(P，T，err_goal，spread)，在网络训练阶段，它可以同时进行参数和结构两个过程的自适应调整，可自适应地增加RBF隐含层单元数以达到目标误差的要求。
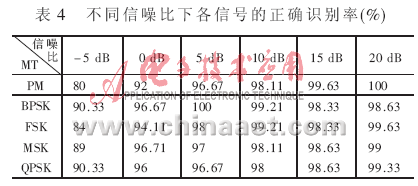
　　进行系统测试，检测正确识别率，表4给出了信噪比分别为-5 dB、0 dB、5 dB、10 dB、15 dB和20 dB情况下5种调制信号的成功识别率。
　　由表4可以看出，采用本文提取的特征参数和神经网络算法，在-5 dB情况下所选5种信号的平均识别成功率为86.73%，最低成功率为80%，最高成功率为90.33%。图3给出了在不同信噪比下，本文提出算法的平均正确识别率。

　　正确识别率与信号采集的长度有很大的关系，而采集时间过长必然导致批处理的数据量增大，其计算复杂度也将提高。由仿真结果可知，本文所提出的算法虽然为减少计算复杂度采取了一定的措施，但由于循环谱算法本身的计算量大，因此，在降低计算复杂度上与其他算法相比所达效果并不明显，但是该算法的识别性能较之有了很大的提高。
　　本文提出基于谱相关所提取的特征参数和改进的径向神经网络识别调制方式的算法，可以在没有载波频率、信息速率等先验信息的情况下对调制方式进行识别，适用于低信噪比的情况，能取得很好的识别效果。
参考文献
[1] GARDNER W A. The spectral correlation theory of cyclo-series[J]. Signal Processing， 1986(11)：13-36.
[2] GARDNER W A， SPOONER C M. Cyclic-spectral analysis for signal detection and modulation recognition[J]. IEEE Trans on Signal Processing，1988：419-424.
[3] 韩国栋，蔡斌，邬江兴.调制分析与识别的谱相关方法[J].系统工程与电子技术，2001，123(13).
[4] 周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005.
[5] GARDNER W A. Measurement of spectral correlation[J]. IEEE Trans on Acoust，Speech， Signal Processing， 1986(34)：1111-1123.
[6] BROWN W， LOOMIS H. Digital implementations of spectral correlation analyzers[J]. IEEE Trans on Signal Processing， 1993(41)：703-720.