摘 要: 针对CMA+DDLMS双模式盲均衡算法对相位不敏感、收敛速度慢、突然切换容易造成误码率升高以及算法不稳定等问题,提出一种基于联合误差控制的变步长双模切换盲均衡算法。与现有双模式算法相比,新算法引入变步长因子有效提高算法收敛速度,同时采用联合绝对剩余误差和判决区域控制的双模切换保证算法的稳健性。采用 16QAM 系统的仿真结果表明,新算法具有抗干扰能力强、收敛精度高和收敛速度快等特点。
关键词: 盲均衡;变步长;VSMCMA-DDLMS算法;最小均方算法;双模切换;判决域
在现代通信系统中,为了在有限频带内传输更多的信息,多采用高效的调制方式进行传输。由于信道的非理想传输特性以及信道传输特性的复杂化等因素的综合作用,使发送序列在传递过程中会产生码间干扰(ISI)和信道间干扰(ICI)。为了保证通信质量,克服码间干扰,就必须采用盲均衡技术以补偿信道特性,从而正确恢复发送序列。均衡的目的是使输出端的输出序列尽可能地接近发送端的发送序列。盲均衡技术的突出特点是仅凭接收序列本身的统计特性来均衡通信信道的特性,而不依靠训练序列。
常数模算法CMA(Constant Modulus Algorithm)和判决引导最小均方误差算法DD-LMS(Decision Directed-LMS)是Bussgang[1]类盲均衡算法中的两种特殊的算法。对于高阶QAM信号,虽然CMA算法可稳健地收敛,但剩余误差却不为零,将会造成较高的误码率。DD-LMS算法虽然剩余误差为零,但却不具备冷启动的能力。参考文献[2]采用CMA算法作为冷启动算法,当其误码率降至某一数量级就切换到DD-LMS算法,该算法存在收敛速度慢、无法克服相位旋转以及误收敛现象等缺点,使其应用受到一定限制。
在修正恒模算法MCMA(Modify-CMA)[4]的基础上,参考文献[5]采用由MCMA盲均衡算法作为冷启动,当判决错误率达到足够低的水平时切换到DD-LMS算法,克服了相位旋转的问题,提高了通信质量,但误码率仍比较高且存在切换不稳定的现象。本文将修正恒模算法和判决引导算法相结合,通过联合绝对剩余误差和判决域实现两种盲均衡算法之间的切换,同时引入了变步长算法。仿真结果表明,该算法不仅具有较快的收敛速度和较好的稳健性,而且具有较高的收敛精度。
1 盲均衡算法
盲均衡系统的等效模型框图如图1所示。




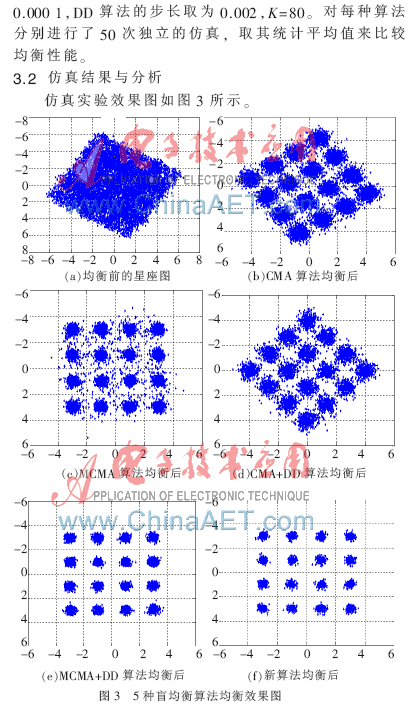
从图3可以看出,在存在信道相位偏移时,CMA算法输出的星座图偏移了一个角度,且CMA+DDLMS双模算法仍然存在相位偏移的现象;MCMA算法和MCMA+DDLMS双模算法以及基于联合误差控制的VS_MCMA +DDLMS算法都很好地消除了相位偏移,且在同样的条件下,MCMA+DDLMS双模算法输出星座图比MCMA紧促密集,VS_MCMA+DDLMS双模算法输出星座图比MCMA+DDLMS要更加紧促,有效地提高了均衡的准确度,实现了更高效的通信。
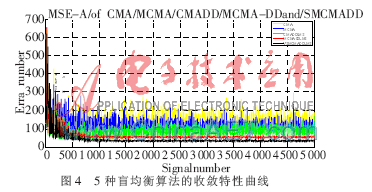
5种盲均衡算法的收敛特性曲线如图4所示。从图4可以看出,CMA算法收敛后,稳态均方误差比较大,且波动较大;MCMA算法在一定程度上降低了稳态均方误差;CMA+DDLMS双模算法的收敛性能有所改善,但均衡后波动仍较大;MCMA+DDLMS双模算法随着算法的收敛均衡波动减小了很多,误码率也有所降低;本文提出的算法在初始阶段由于采用变步长算法控制,初始阶段波动较大,加快了收敛速度,算法趋于收敛后波动较小,同时在MCMA+DDLMS双模算法的基础上极大地降低了误码率。
本文在MCMA的基础上提出了一种基于联合误差控制的VS_MCMA+DDLMS双模式盲均衡算法,该算法根据均衡输出信号在星座图上所处区域以及剩余误差函数进行切换,将VS_MCMA和DDLMS算法有效结合起来,增强了算法的稳健性,提高了算法的收敛速度。采用16QAM信号的仿真结果表明,该算法可较好地纠正信号的相位误差,均衡后的星座图更加紧促密集,有效降低了稳态均方误差,能更好地解决复杂系统的信道均衡问题。
参考文献
[1] De Castro F C C, De Castro M C F, ARANTES D S. Concurrent blind deconvolution for channel equalization[C].IEEE International Conference on Communications, ICC 2001, 2001,2: 366-371.
[2] Zhang Jiaqi, Ge Ning. Joint CMA+DDLMS blind equalization algorithm[J]. Tsinghua University(Sci &Tech), 2009, 49(10):108-111.
[3] JOHN G, PROAKIS D. Digital Communications, Fourth Edition [M]. New York: McGraw-Hill,2001.
[4] 钟华,金国平,郑林华,等.改进MCMA盲均衡算法[J].信号处理,2009,25(5):766-770.
[5] Guo Yuanshu, Yue Lei, Yao Bobin. Dual mode blind equalization algorithm based on dual-mode MCMA+DD [J]. Acta Photonica Sinica, 2009,38(1):2702-2706.
[6] Zhang Liyi, Chen Lei, Sun Yunshan. Variable step size CMA blind equalization based on nonlinear function of error signal[C]. IEEE International Conference on Commu- nications and Mobile Computing, 2009: 396-399.
[7] 唐虹,李明,冯文江.适用于高阶QAM系统的双模式盲均衡算法[J].电子技术应用,2011,37(2):113-116.
[8] 张晓娟,关明明,吴长奇.基于点判决域的多模盲均衡算法及其FPGA实现[J].电子技术应用,2011(2):51-54.

